자동제어 | 시스템의 안정한 범위구하기 |
페이지 정보
작성자 cemtool 작성일14-04-22 13:28 조회57,181회 댓글57건본문
다음과 같은 루프전달함수를 가진 제어시스템을 생각하자.
«풀이»
먼저 근궤적선도를 통해 시스템이 안정하기 위한 K의 임계값을 구하고, 실제로 몇 개의 K에 대해서 Nyquist 선도 또는 Routh-Hurwitz 판별법을 통해 결과를 확인해보도록 하자. 다음은 주어진 시스템에 대한 근궤적선도이다.
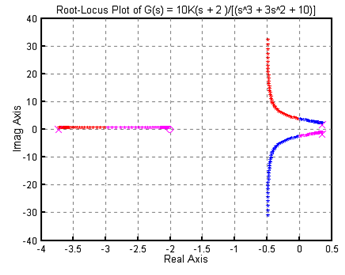
그림 7-의 근궤적선도를 보면 K가 어떤 K값일 때 허수축을 지나고 있다. 이 때의 값이 시스템이 안정하기 위한 임계값이 된다. CEMTool을 사용하여 K의 임계값을 찾기는 쉽지 않다. 따라서, 손으로 직접 계산하거나 여러 번의 시행착오를 통해 그 값을 구해야 한다. 이 예제의 경우에는 K=1일 때 근궤적선도상의 허수축을 지난다. 즉, 0<K<1일 때는 불안정, K=1일 때는 임계안정, K>1일 때는 안정하다. 이 사실을 K=0.5, 1, 2의 예를 통해 확인해보자. 각 K의 값에 대하여 안정도를 판별할 때에는 Nyquist 선도나 Routh 표를 이용하면 된다.
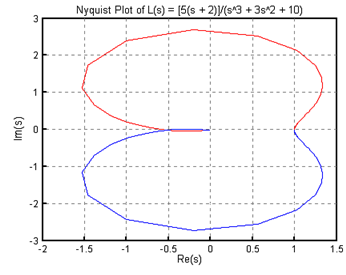
(1) K=0.5일 때
- ex7_5.cem
// Nyquist plotnum = 5*[1 2]; den = [1 3 0 10]; nyquist(num, den); title("Nyquist Plot of L(s) = [5(s + 2)]/(s^3 + 3s^2 + 10)")// Routh table routh([0 0 num] + den)
1.0000 5.0000
3.0000 20.0000
-1.6667 0.0000
20.0000 0.0000
프로그램을 실행시키면 그림 7-과 같은 Nyquist 선도를 얻을 수 있다. 시스템이 안정하기 위해서는 이
이어야 하나 실제 값은
이므로 시스템은 불안정하다. 또한 Routh 표에서도 두 번의 부호변화가 있으므로 시스템이 불안정함을 알 수 있다.
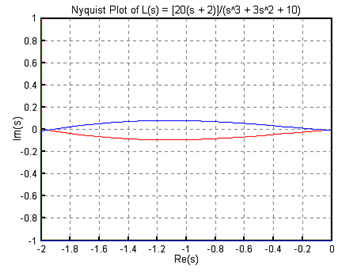
(2) K=1일 때
- ex7_5.cem
// Nyquist plotnum = 10*[1 2]; den = [1 3 0 10]; nyquist(num, den); title("Nyquist Plot of L(s) = [10(s + 2)]/(s^3 + 3s^2 + 10)")// Routh table routh([0 0 num] + den)
Special case : one row in Routh table is zero!
1 10
3 30
0 0
그림 7-는 결과로 나온 그래프의 x축 범위를 [-2,0]으로, y축의 범위를 [-1,1]로 조정한 것이다.
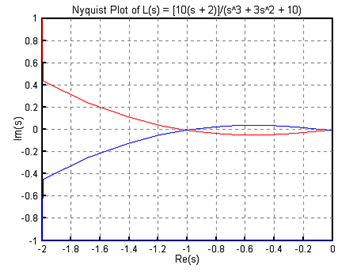
Nyquist 선도가 임계점 (-1,j0)을 지나므로 시스템은 임계안정하다. 이 때에는 Routh 표에서 특별한 경우가 나오므로 CEMTool을 통해서 완전한 Routh 표를 구할 수 없고 교재에서 설명한 방법 등을 사용하여 다시 계산해야 한다.
(3) K=2일 때
- ex7_5.cem
// Nyquist plotnum = 20*[1 2]; den = [1 3 0 10]; nyquist(num, den); title("Nyquist Plot of L(s) = [20(s + 2)]/(s^3 + 3s^2 + 10)")// Routh table routh([0 0 num] + den)
1.0000 20.0000
3.0000 50.0000
3.3333 0.0000
50.0000 0.0000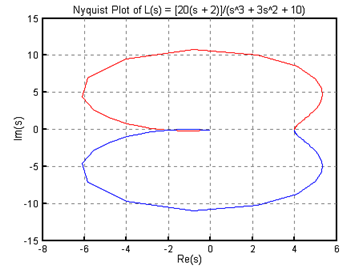
댓글목록
yitao69님의 댓글
yitao69 작성일
http://www.yeezyboost350--v2.us.com/ yeezy shoes
http://www.coachbags-outlet.us.com/ coach wallet
http://www.burberrys.org.uk/ burberry handbags
http://www.burberry--scarf.us.com/ burberry outlet
http://www.fitflops-sale.us.com/ fitflop
http://www.jordan11spacejams.us.com/ jordan shoes
http://www.goyardbackpack.us.com/ goyard
http://www.hermes--belt.us.com/ hermes belt men
http://www.kyrie-irving-shoes.us.com/ nike kyrie
http://www.supreme--clothing.us.com/ supreme
http://www.salomon--shoes.us.com/ Salomon xa pro 3d
http://www.asicss.us.com/ asics
http://www.pandorasjewelry.co.uk/ pandora uk
http://www.michael-kors-bags.us.com/ michael kors bags
http://www.james-hardenshoes.us.com/ harden shoes
http://www.adidas-superstarshoes.us.com/ adidas originals superstar
http://www.adidasoriginalsultraboost.us.com/ ultra boost uncaged
http://www.cartier-bracelet.us.com/ cartier bracelet
http://www.fitflopsshoes.us.com/ fitflops clearance
http://www.skecherss.us.com/ skechers
http://www.monclerjacketwomens.us.com/ moncler jacket
http://www.monclers.uk/ moncler
http://www.burberry-bags.us.com/ burberry scarf
http://www.nikelebron15.us.com/ lebron 15
http://www.nikeairmax270.org.uk/ nike air max 270
http://www.monclerjacketmens.us.com/ moncler,moncler jacket
http://www.jordan11.co.uk/ jordan shoes
http://www.nike-huaraches.us.com/ nike air huarache
http://www.celines.us.com/ celine handbags
http://www.ray--bansunglassess.us.com/ ray ban sunglasses
http://www.chrome--hearts.us.com/ chrome hearts ring
http://www.new--balance.us.com/ new balance running shoes women
http://www.balenciagas-sneakers.us.com/ balenciaga sneakers
http://www.michaelkors-handbagss.us.com/ michael kors handbags
http://www.redbottom--shoes.us.com/ red bottom shoes
http://www.birkenstock--sandals.us.com/ birkenstock outlet
http://www.northface-jacket.us.com/ north face
http://www.adidas-yeezy-shoes.us.com/ Yeezy
http://www.airmax95.co.uk/ nike air max 95 mens
http://www.ugg--slippers.us.com/ uggs on sale
http://www.mulberry-handbags.us.com/ mulberry bag
http://www.mbts.us.com/ mbt mens shoes
http://www.pandoraearrings.us.com/ pandora
http://www.longchampbag.us.com/ longchamp le pliage
http://www.air-max-97.us.com/ air max 97 womens
http://www.nike-airmax-2018.us.com/ air max
http://www.airmax-2018.us.com/ nike air max 2018
http://www.pandoras-uk.co.uk/ pandora jewelry
http://www.pandorauk.us.com/ pandora jewelry
http://www.asics--shoes.us.com/ asics shoes
http://www.air-max-270.us.com/ nike air max 270 men
http://www.nikeair-max90.co.uk/ nike air max
http://www.mcm--bags.us.com/ mcm bags
http://www.chromehearts-jewelry.us.com/ chrome hearts bracelet
http://www.adidas--shoes.co.uk/ adidas
http://www.airmax270.co.uk/ nike vapormax
http://www.longchampbackpack.us.com/ longchamp backpack
http://www.uggsformen.us.com/ ugg,ugg slippers
http://www.vapormaxs.us.com/ nike vapormax
http://www.pumarihannafenty.us.com/ puma fenty
http://www.moncler--jacket.us.com/ moncler jacket womens
http://www.jordans11shoes.us.com/ air jordan
http://www.oakley--glasses.us.com/ oakley prescription sunglasses
http://www.goyardbag.us.com/ goyard tote
http://www.ultra--boost.us.com/ adidas originals ultra boost
http://www.huaraches.us.com/ nike air huarache
http://www.nikeairmax-90.us.com/ nike air max
http://www.jimmychooheels.us.com/ jimmy choo trainers
http://www.nike--vapormax.us.com/ air vapormax
http://www.pandora--jewelrys.us.com/ pandora earrings
http://www.yeezyboost350shoes.us.com/ yeezy boost 350 v2
http://www.jordanretro11-shoes.us.com/ jordan shoes
http://www.skechersuk.co.uk/ skechers boots
http://www.barbourjackets.co.uk/ barbour
http://www.yeezyboost350v2.co.uk/ adidas yeezy
http://www.salvatore-ferragamo.us.com/ ferragamo shoes men
http://www.pandoras-jewelrys.us.com/ pandora rings
http://www.pandora-jewelrysale.us.com/ pandora charms
http://www.truereligion--jeans.us.com/ true religion jeans for women
http://www.balenciaga--shoes.us.com/ balenciaga women
http://www.kd10-shoes.us.com/ kd shoes
http://www.adidasoriginalsnmd.us.com/ adidas nmd r1
http://www.skechers--shoes.us.com/ skechers women
http://www.curry4-shoes.us.com/ curry shoes
http://www.air-max-95.us.com/ air max 95
http://www.adidasyeezys.org.uk/ yeezy shoes
http://www.air-max-90.us.com/ nike air max 90
http://www.nike--shoes.co.uk/ nike outlet
http://www.pandorajewelryscharms.us.com/ pandora jewelry
http://www.airmax90shoes.us.com/ nike air max 90
http://www.adidasyeezy-350.us.com/ yeezy boost 350
http://www.louboutinredbottoms.us.com/ christian louboutin
http://www.prada--bags.us.com/ prada handbags
http://www.valentino--shoes.us.com/ valentino
http://www.supremeshirt.us.com/ supreme shirt
http://www.pandora-charmsjewelry.us.com/ pandora charms
http://www.uggs--boots.us.com/ ugg boots
http://www.polo-ralphlauren-outlet.us.com/ polo ralph lauren outlet
http://www.pandorajewelryrings.us.com/ pandora jewelry
http://www.adidasnmdrunnerr1.us.com/ nmd adidas
http://www.nikeairvapormaxflyknit.us.com/ nike air force 1
http://www.coach--bags.us.com/ coach
http://www.stephen-curry-shoes.us.com/ curry shoes
http://www.fitflop--sandals.us.com/ fitflop sandals
http://www.kyrie-4.us.com/ kyire 4
http://www.nikeair-max.co.uk/ nike air max
http://www.mcms.us.com/ mcm handbags
http://www.northfacejacketoutlets.us.com/ north face jacket
http://www.adidasnmds.co.uk/ adidas originals nmd
http://www.salomonshoes.co.uk/ salomon boots
http://www.katespadebags.us.com/ kate spade handbags
http://www.katespadepurses.us.com/ kate spade bags
http://www.nikeairmax-97.us.com/ air max 97 gold
http://www.ferragamoshoess.us.com/ ferragamo shoes men
http://www.katespade--outlet.us.com/ kate spade outlet
http://www.rayban-glasses.us.com/ ray ban glasses
http://www.swarovskisjewelry.us.com/ swarovski necklace
http://www.adidasnmd-womens.us.com/ adidas originals nmd
http://www.prada--handbags.us.com/ prada purse
http://www.uggs-forwomen.us.com/ ugg
http://www.birkenstocksandalssale.us.com/ birkenstock shoes
http://www.ray--ban.us.com/ ray ban
http://www.redbottoms-louboutin.us.com/ red bottom shoes
http://www.lacosteshirts.us.com/ lacoste shoes
http://www.oakley--sunglassess.us.com/ oakley
http://www.under-armour-shoes.us.com/ under armour jackets
http://www.nikeairmax-95.us.com/ nike air max 95
http://www.fitflop--shoes.us.com/ fitflop
http://www.bvlgaris.us.com/ bvlgari
http://www.ralphlauren--polo.us.com/ ralph lauren outlet
http://www.mulberrys.org.uk/ mulberry purse
http://www.rayban--glasses.us.com/ ray ban
http://www.barbours.org.uk/ barbour jacket
http://www.jordan--11.us.com/ jordan retro 11
http://www.montblancs.us.com/ mont blanc pens
http://www.nikekdshoes.us.com/ kd 9
http://www.christianlouboutinredbottoms.us.com/ louboutin
http://www.pandora-jewelrybracelet.us.com/ pandora,pandora charms
http://www.ed-hardys.us.com/ ed hardy
http://www.true--religion.us.com/ true religion
http://www.adidas-ultraboost.us.com/ adidas ultra boost
http://www.nike-airmax270.us.com/ air max 270
http://www.adidas-yeezyboost350.us.com/ adidas yeezy
http://www.airjordan11spacejam.us.com/ jordan shoes
http://www.swarovskis.us.com/ swarovski bracelet
http://www.eccoshoesoutlets.us.com/ ecco outlet
http://www.moncler-coat.us.com/ moncler
http://www.ralphlaurenspoloshirts.us.com/ ralph lauren outlet
http://www.salomon-boots.us.com/ salomon xa pro 3d
http://www.hermesbirkin-handbags.us.com/ Hermes Handbags
http://www.monclerjacket.org.uk/ moncler coat
http://www.pandora--rings.us.com/ Pandora Rings
http://www.salomonspeedcross3.us.com/ salomon shoes
http://www.kevin-durant-shoes.us.com/ kd shoes
http://www.polo-ralph-lauren.org.uk/ ralph lauren shirts
http://www.nikeairmax97.co.uk/ nike air max
http://www.lebron15-shoes.us.com/ lebron 15
http://www.chromeheartsjewelrys.us.com/ chrome hearts jewelry
xiaodai79님의 댓글
xiaodai79 작성일
http://www.nike--vapormax.us.com/ air vapormax
http://www.adidasnmdrunnerr1.us.com/ nmd adidas
http://www.katespadebags.us.com/ kate spade
http://www.katespade--outlet.us.com/ kate spade outlet
http://www.jordanretro11-shoes.us.com/ jordan 11
http://www.kyrie-irving-shoes.us.com/ kyrie irving shoes
http://www.fitflop--shoes.us.com/ fitflop uk
http://www.burberry-bags.us.com/ burberry wallet
http://www.bvlgaris.us.com/ bulgari jewelry
http://www.celines.us.com/ celine,celine bag
http://www.nikeairmax-95.us.com/ air max 95
http://www.airmax270.co.uk/ off white nike
http://www.ray--bansunglassess.us.com/ ray ban
http://www.swarovskisjewelry.us.com/ swarovski necklace
http://www.nike--shoes.co.uk/ nike outlet
http://www.ray--ban.us.com/ ray ban eyeglasses
http://www.truereligion--jeans.us.com/ true religion jeans men
http://www.yeezyboost350v2.co.uk/ yeezy shoes
http://www.pandoraearrings.us.com/ pandora jewelry
http://www.airmax95.co.uk/ nike air max 90
http://www.polo-ralphlauren-outlet.us.com/ ralph lauren polo shirts
http://www.stephen-curry-shoes.us.com/ stephen curry shoes
http://www.adidas-ultraboost.us.com/ adidas ultra boost
http://www.true--religion.us.com/ true religion jeans for women
http://www.fitflop--sandals.us.com/ fitflop sale
http://www.oakley--sunglassess.us.com/ oakley glasses
http://www.burberry--scarf.us.com/ burberry bags
http://www.nikeairmax-90.us.com/ nike vapormax
http://www.moncler-coat.us.com/ moncler coat
http://www.mcms.us.com/ mcm wallet
http://www.salomonspeedcross3.us.com/ salomon speedcross 4
http://www.adidas-superstarshoes.us.com/ adidas superstar shoes
http://www.nikeair-max90.co.uk/ nike air max 95
http://www.salvatore-ferragamo.us.com/ ferragamo shoes
http://www.nikelebron15.us.com/ lebron
http://www.chrome--hearts.us.com/ chrome hearts ring
http://www.fitflopsshoes.us.com/ fitflop
http://www.pandorauk.us.com/ pandora
http://www.fitflops-sale.us.com/ fitflop shoes
http://www.monclerjacketwomens.us.com/ moncler jacket
http://www.under-armour-shoes.us.com/ under armour shirts
http://www.yeezyboost350shoes.us.com/ yeezy boost 350 v2
http://www.ralphlauren--polo.us.com/ ralph lauren shirts
http://www.nikeairmax-97.us.com/ air max 97
http://www.adidasoriginalsultraboost.us.com/ adidas ultra boost
http://www.redbottoms-louboutin.us.com/ red bottoms
http://www.prada--handbags.us.com/ prada
http://www.chromehearts-jewelry.us.com/ chrome hearts pendant
http://www.mbts.us.com/ mbt shoes
http://www.air-max-95.us.com/ air max 95
http://www.monclers.uk/ moncler jacket mens
http://www.barbours.org.uk/ barbour outlet
http://www.new--balance.us.com/ new balance 574
http://www.nikeairmax270.org.uk/ nike air max 95
http://www.jordans11shoes.us.com/ jordan shoes
http://www.birkenstock--sandals.us.com/ birkenstock sale
http://www.nike-airmax270.us.com/ nike air max
http://www.nike-airmax-2018.us.com/ air max 2018
http://www.vapormaxs.us.com/ nike vapormax
http://www.airmax-2018.us.com/ nike air max 2018
http://www.lebron15-shoes.us.com/ basketball shoes
http://www.nike-huaraches.us.com/ nike huarache
http://www.ultra--boost.us.com/ adidas ultra boost uncaged
http://www.uggs-forwomen.us.com/ uggs for women
http://www.kyrie-4.us.com/ kyire 3
http://www.louboutinredbottoms.us.com/ christian louboutin
http://www.coach--bags.us.com/ coach outlet
http://www.northface-jacket.us.com/ north face jacket
http://www.airmax90shoes.us.com/ nike air max 95
http://www.redbottom--shoes.us.com/ louboutin
http://www.birkenstocksandalssale.us.com/ birkenstock shoes
http://www.salomon--shoes.us.com/ Salomon Boots
http://www.balenciagas-sneakers.us.com/ balenciaga shoes
http://www.uggs--boots.us.com/ uggs for women
http://www.mcm--bags.us.com/ mcm
http://www.montblancs.us.com/ mont blanc outlet
http://www.mulberrys.org.uk/ mulberry bayswater
http://www.curry4-shoes.us.com/ under armour stephen curry
http://www.kevin-durant-shoes.us.com/ kd 10
http://www.pandora-charmsjewelry.us.com/ pandora bracelet
http://www.ralphlaurenspoloshirts.us.com/ ralph lauren shirts
http://www.air-max-270.us.com/ air max 270
http://www.pandora--rings.us.com/ Pandora Jewelry
http://www.adidas--shoes.co.uk/ adidas outlet
http://www.ed-hardys.us.com/ ed hardy clothing
http://www.james-hardenshoes.us.com/ harden shoes
http://www.jordan--11.us.com/ jordan retro
http://www.skechersuk.co.uk/ skechers outlet
http://www.longchampbag.us.com/ longchamp le pliage
http://www.ugg--slippers.us.com/ ugg boots
http://www.pandoras-uk.co.uk/ pandora bracelet
http://www.supreme--clothing.us.com/ supreme shirt
http://www.katespadepurses.us.com/ kate spade
http://www.goyardbackpack.us.com/ goyard bag
http://www.huaraches.us.com/ nike air huarache
http://www.airjordan11spacejam.us.com/ air jordan
http://www.skechers--shoes.us.com/ skechers
http://www.longchampbackpack.us.com/ longchamp handbag
http://www.air-max-97.us.com/ air max 97
http://www.asicss.us.com/ asics outlet
http://www.jimmychooheels.us.com/ jimmy choo trainers
http://www.pumarihannafenty.us.com/ puma shoes
http://www.pandorasjewelry.co.uk/ pandora charm
http://www.air-max-90.us.com/ air max 90
http://www.adidasyeezy-350.us.com/ yeezy boost
http://www.uggsformen.us.com/ ugg boots
http://www.kd10-shoes.us.com/ kd 9
http://www.valentino--shoes.us.com/ red valentino
http://www.michaelkors-handbagss.us.com/ mk handbags
http://www.northfacejacketoutlets.us.com/ womens north face jacket
http://www.nikeairmax97.co.uk/ nike shoes
http://www.monclerjacket.org.uk/ moncler jacket
http://www.jordan11.co.uk/ air jordan
http://www.salomon-boots.us.com/ salomon
http://www.pandorajewelryscharms.us.com/ pandora jewelry
http://www.adidas-yeezy-shoes.us.com/ Yeezy Boost 350 V2
http://www.salomonshoes.co.uk/ salomon skis
http://www.adidas-yeezyboost350.us.com/ yeezy shoes
http://www.nikeairvapormaxflyknit.us.com/ nike vapormax
http://www.jordan11spacejams.us.com/ space jam 11
http://www.adidasnmds.co.uk/ nmd
http://www.nikekdshoes.us.com/ kevin durant shoes
http://www.supremeshirt.us.com/ supreme shirt
http://www.ferragamoshoess.us.com/ ferragamo shoes
http://www.skecherss.us.com/ skechers outlet
http://www.hermes--belt.us.com/ hermes belt women
http://www.nikeair-max.co.uk/ nike air max 95
http://www.mulberry-handbags.us.com/ mulberry
http://www.adidasnmd-womens.us.com/ adidas originals nmd
http://www.pandora-jewelrysale.us.com/ pandora bracelet
http://www.adidasoriginalsnmd.us.com/ adidas nmd r1
http://www.pandoras-jewelrys.us.com/ pandora jewelry
http://www.rayban--glasses.us.com/ ray ban
http://www.chromeheartsjewelrys.us.com/ chrome hearts t shirt
http://www.michael-kors-bags.us.com/ michael kors
http://www.cartier-bracelet.us.com/ cartier
http://www.burberrys.org.uk/ burberry bags
http://www.pandorajewelryrings.us.com/ pandora earrings
http://www.yeezyboost350--v2.us.com/ yeezy boost 350
http://www.monclerjacketmens.us.com/ moncler coat
http://www.pandora-jewelrybracelet.us.com/ pandora rings
http://www.eccoshoesoutlets.us.com/ ecco outlet
http://www.adidasyeezys.org.uk/ yeezy boost 350 v2
http://www.rayban-glasses.us.com/ ray ban glasses
http://www.swarovskis.us.com/ swarovski necklace
http://www.asics--shoes.us.com/ asics running shoes
http://www.prada--bags.us.com/ prada wallet
http://www.hermesbirkin-handbags.us.com/ Hermes Birkin Bags
http://www.coachbags-outlet.us.com/ coach handbags
http://www.barbourjackets.co.uk/ barbour wax jacket
http://www.oakley--glasses.us.com/ oakley
http://www.lacosteshirts.us.com/ lacoste shoes
http://www.christianlouboutinredbottoms.us.com/ christian louboutin
http://www.balenciaga--shoes.us.com/ balenciaga bag
http://www.moncler--jacket.us.com/ moncler jacket womens
http://www.goyardbag.us.com/ goyard backpack
http://www.pandora--jewelrys.us.com/ pandora jewelry
http://www.polo-ralph-lauren.org.uk/ polo ralph lauren
banmei40님의 댓글
banmei40 작성일
http://www.skechersuk.co.uk/ skechers
http://www.asics--shoes.us.com/ asics shoes
http://www.pandoraearrings.us.com/ pandora rings
http://www.jordan11spacejams.us.com/ jordan retro 12
http://www.vapormaxs.us.com/ vapormax
http://www.prada--handbags.us.com/ prada shoes
http://www.skecherss.us.com/ skechers outlet
http://www.supremeshirt.us.com/ supreme clothing
http://www.hermesbirkin-handbags.us.com/ Hermes Belts
http://www.ray--ban.us.com/ ray ban glasses
http://www.northfacejacketoutlets.us.com/ womens north face jacket
http://www.adidasoriginalsultraboost.us.com/ adidas ultra boost
http://www.katespade--outlet.us.com/ kate spade bags
http://www.air-max-95.us.com/ air max 95 black
http://www.balenciagas-sneakers.us.com/ balenciaga
http://www.michaelkors-handbagss.us.com/ michael kors purse
http://www.burberry--scarf.us.com/ burberry bags
http://www.nikeair-max90.co.uk/ nike air max
http://www.adidasyeezy-350.us.com/ adidas yeezy
http://www.moncler-coat.us.com/ moncler jacket
http://www.monclers.uk/ moncler jacket womens
http://www.mcms.us.com/ mcm backpack
http://www.curry4-shoes.us.com/ stephen curry shoes
http://www.ray--bansunglassess.us.com/ ray ban sunglasses
http://www.christianlouboutinredbottoms.us.com/ christian louboutin
http://www.barbours.org.uk/ barbour outlet
http://www.longchampbackpack.us.com/ longchamp
http://www.air-max-90.us.com/ nike air max
http://www.prada--bags.us.com/ prada wallet
http://www.pandora-jewelrysale.us.com/ pandora jewelry official site
http://www.mbts.us.com/ mbt
http://www.adidas-yeezyboost350.us.com/ yeezy boost 350 v2
http://www.adidas-superstarshoes.us.com/ adidas
http://www.rayban--glasses.us.com/ ray ban wayfarer
http://www.michael-kors-bags.us.com/ michael kors bags
http://www.chromehearts-jewelry.us.com/ chrome hearts clothing
http://www.nike--shoes.co.uk/ nike air max 97
http://www.nikeairmax270.org.uk/ nike air max 97
http://www.kd10-shoes.us.com/ kevin durant shoes
http://www.lebron15-shoes.us.com/ lebron james shoes
http://www.adidasnmdrunnerr1.us.com/ adidas nmd r1
http://www.salomon-boots.us.com/ salomon xa pro 3d
http://www.nike-huaraches.us.com/ huarache shoes
http://www.adidas-ultraboost.us.com/ adidas ultra uncaged
http://www.monclerjacket.org.uk/ moncler jacket mens
http://www.oakley--glasses.us.com/ oakley glasses
http://www.uggs-forwomen.us.com/ ugg slippers
http://www.nikeair-max.co.uk/ nike air max 95
http://www.jordans11shoes.us.com/ jordan shoes
http://www.montblancs.us.com/ mont blanc pens
http://www.pandorauk.us.com/ pandora charms
http://www.uggsformen.us.com/ uggs for men
http://www.new--balance.us.com/ new balance
http://www.ferragamoshoess.us.com/ ferragamo shoes men
http://www.air-max-97.us.com/ air max 97 womens
http://www.pandora--jewelrys.us.com/ pandora earrings
http://www.salomon--shoes.us.com/ Salomon xa pro 3d
http://www.pandora-jewelrybracelet.us.com/ pandora,pandora charms
http://www.under-armour-shoes.us.com/ under armour shoes
http://www.jordanretro11-shoes.us.com/ jordan retro 11
http://www.yeezyboost350--v2.us.com/ yeezy boost 350
http://www.goyardbag.us.com/ goyard bag
http://www.salvatore-ferragamo.us.com/ ferragamo shoes men
http://www.nikelebron15.us.com/ nike lebron
http://www.nikeairmax-90.us.com/ nike air max
http://www.true--religion.us.com/ true religion jeans men
http://www.redbottom--shoes.us.com/ louboutin
http://www.coachbags-outlet.us.com/ coach purses
http://www.chrome--hearts.us.com/ chrome hearts t shirt
http://www.kyrie-4.us.com/ kyire 4
http://www.burberry-bags.us.com/ burberry wallet
http://www.goyardbackpack.us.com/ goyard bag
http://www.airmax-2018.us.com/ air max 2018
http://www.uggs--boots.us.com/ ugg slippers
http://www.ralphlaurenspoloshirts.us.com/ ralph lauren polo shirts
http://www.mulberrys.org.uk/ mulberry purse
http://www.monclerjacketwomens.us.com/ moncler coat
http://www.pandora--rings.us.com/ Pandora Charms
http://www.birkenstock--sandals.us.com/ birkenstock outlet
http://www.eccoshoesoutlets.us.com/ ecco outlet
http://www.nike-airmax270.us.com/ air max 270
http://www.skechers--shoes.us.com/ skechers boots
http://www.rayban-glasses.us.com/ ray ban glasses
http://www.fitflops-sale.us.com/ fitflop sandals
http://www.moncler--jacket.us.com/ moncler coat
http://www.fitflop--shoes.us.com/ fitflop uk
http://www.nike--vapormax.us.com/ nike air vapormax
http://www.nikeairmax-95.us.com/ nike air max 95
http://www.celines.us.com/ celine wallet
http://www.hermes--belt.us.com/ hermes belt
http://www.birkenstocksandalssale.us.com/ birkenstock sandals
http://www.pandoras-uk.co.uk/ pandora rings
http://www.stephen-curry-shoes.us.com/ stephen curry
http://www.ugg--slippers.us.com/ ugg boots
http://www.nikekdshoes.us.com/ kd shoes
http://www.redbottoms-louboutin.us.com/ red bottom shoes
http://www.kevin-durant-shoes.us.com/ kd 11
http://www.monclerjacketmens.us.com/ moncler coat
http://www.balenciaga--shoes.us.com/ balenciaga
http://www.katespadepurses.us.com/ kate spade
http://www.adidasoriginalsnmd.us.com/ adidas nmd
http://www.salomonshoes.co.uk/ salomon xa pro 3d
http://www.adidas-yeezy-shoes.us.com/ Adidas Yeezy
http://www.james-hardenshoes.us.com/ james harden
http://www.pandora-charmsjewelry.us.com/ pandora charms
http://www.nikeairmax97.co.uk/ nike shoes
http://www.air-max-270.us.com/ nike air max 270 women
http://www.chromeheartsjewelrys.us.com/ chrome hearts
http://www.pandorajewelryscharms.us.com/ pandora jewelry
http://www.salomonspeedcross3.us.com/ salomon shoes
http://www.truereligion--jeans.us.com/ true religion jeans for women
http://www.adidasyeezys.org.uk/ yeezy shoes
http://www.airmax95.co.uk/ nike air max 95
http://www.yeezyboost350shoes.us.com/ yeezy boost 350 v2
http://www.nikeairmax-97.us.com/ air max 97 gold
http://www.louboutinredbottoms.us.com/ christian louboutin shoes
http://www.polo-ralph-lauren.org.uk/ polo ralph lauren
http://www.pandorajewelryrings.us.com/ pandora necklace
http://www.adidasnmds.co.uk/ adidas nmd
http://www.jordan--11.us.com/ jordan retro 11
http://www.jordan11.co.uk/ jordan retro 11
http://www.kyrie-irving-shoes.us.com/ kyrie irving
http://www.asicss.us.com/ asics running shoes
http://www.mcm--bags.us.com/ mcm bags
http://www.adidas--shoes.co.uk/ adidas boost
http://www.barbourjackets.co.uk/ barbour wax jacket
http://www.ralphlauren--polo.us.com/ polo ralph lauren
http://www.polo-ralphlauren-outlet.us.com/ polo
http://www.coach--bags.us.com/ coach purses
http://www.huaraches.us.com/ nike air huarache
http://www.supreme--clothing.us.com/ supreme shirt
http://www.pandoras-jewelrys.us.com/ pandora
http://www.katespadebags.us.com/ kate spade handbags
http://www.valentino--shoes.us.com/ valentino
http://www.yeezyboost350v2.co.uk/ yeezy shoes
http://www.cartier-bracelet.us.com/ cartier jewelry
http://www.pandorasjewelry.co.uk/ pandora jewelry
http://www.ed-hardys.us.com/ ed hardy
http://www.oakley--sunglassess.us.com/ oakley eyeglasses
http://www.airmax270.co.uk/ nike vapormax
http://www.swarovskisjewelry.us.com/ swarovski bracelet
http://www.swarovskis.us.com/ swarovski earrings
http://www.fitflopsshoes.us.com/ fitflop
http://www.fitflop--sandals.us.com/ fitflop shoes
http://www.mulberry-handbags.us.com/ mulberry handbags
http://www.burberrys.org.uk/ burberry
http://www.nike-airmax-2018.us.com/ nike air max
http://www.pumarihannafenty.us.com/ fenty puma shoes
http://www.adidasnmd-womens.us.com/ adidas nmd
http://www.ultra--boost.us.com/ adidas ultra boost uncaged
http://www.airjordan11spacejam.us.com/ jordan retro 11
http://www.nikeairvapormaxflyknit.us.com/ nike air max 90
http://www.jimmychooheels.us.com/ jimmy choo trainers
http://www.bvlgaris.us.com/ bvlgari sunglasses
http://www.longchampbag.us.com/ longchamp
http://www.northface-jacket.us.com/ north face coats
http://www.lacosteshirts.us.com/ lacoste sale
http://www.airmax90shoes.us.com/ nike air max
binglu37님의 댓글
binglu37 작성일
http://www.longchampbag.us.com/ longchamp backpack
http://www.rayban-glasses.us.com/ ray ban eyeglasses
http://www.adidasoriginalsultraboost.us.com/ ultra boost uncaged
http://www.nikeairvapormaxflyknit.us.com/ nike air max 90
http://www.nikekdshoes.us.com/ kd 10
http://www.nikeairmax-90.us.com/ air max 90
http://www.hermesbirkin-handbags.us.com/ Hermes Handbags
http://www.adidasnmds.co.uk/ adidas nmd womens
http://www.chrome--hearts.us.com/ chrome hearts bracelet
http://www.kd10-shoes.us.com/ kd 9
http://www.redbottoms-louboutin.us.com/ louboutin
http://www.christianlouboutinredbottoms.us.com/ red bottom shoes
http://www.kyrie-4.us.com/ nike kyire
http://www.fitflopsshoes.us.com/ fitflop sale
http://www.mulberry-handbags.us.com/ mulberry bag
http://www.katespadepurses.us.com/ kate spade purses
http://www.nikeair-max.co.uk/ nike air max 270
http://www.skechers--shoes.us.com/ skechers
http://www.fitflop--sandals.us.com/ fitflop sale
http://www.pandoraearrings.us.com/ pandora charms
http://www.kevin-durant-shoes.us.com/ kd 10
http://www.yeezyboost350v2.co.uk/ yeezy boost 350
http://www.burberrys.org.uk/ burberry backpack
http://www.goyardbag.us.com/ goyard backpack
http://www.swarovskis.us.com/ swarovski jewelry
http://www.nikeairmax97.co.uk/ nike air max 90
http://www.adidas-ultraboost.us.com/ yeezy boost
http://www.airmax270.co.uk/ air max 270
http://www.fitflops-sale.us.com/ fitflops clearance
http://www.uggs-forwomen.us.com/ ugg boots
http://www.lebron15-shoes.us.com/ lebron 15
http://www.birkenstocksandalssale.us.com/ birkenstock sandals
http://www.kyrie-irving-shoes.us.com/ kyrie 4
http://www.adidasyeezy-350.us.com/ yeezy
http://www.celines.us.com/ celine handbags
http://www.supremeshirt.us.com/ supreme clothing
http://www.nike-airmax270.us.com/ air max
http://www.airjordan11spacejam.us.com/ air jordan 11 space jam
http://www.ray--ban.us.com/ ray ban aviator sunglasses
http://www.balenciagas-sneakers.us.com/ balenciaga sneakers
http://www.bvlgaris.us.com/ bvlgari handbags
http://www.mbts.us.com/ mbt
http://www.monclerjacketwomens.us.com/ moncler coat
http://www.air-max-97.us.com/ air max 97
http://www.salomonshoes.co.uk/ salomon skis
http://www.ed-hardys.us.com/ ed hardy shirt
http://www.pandora--jewelrys.us.com/ pandora rings
http://www.moncler--jacket.us.com/ moncler coat
http://www.jordan--11.us.com/ air jordan
http://www.skecherss.us.com/ skechers outlet
http://www.jordans11shoes.us.com/ jordan 11 space jam
http://www.fitflop--shoes.us.com/ fitflop uk
http://www.under-armour-shoes.us.com/ under armour
http://www.coachbags-outlet.us.com/ coach wallet
http://www.barbourjackets.co.uk/ barbour
http://www.nikeairmax-95.us.com/ air max 95 black
http://www.barbours.org.uk/ barbour wax jacket
http://www.yeezyboost350shoes.us.com/ yeezy
http://www.oakley--glasses.us.com/ oakley eyeglasses
http://www.ugg--slippers.us.com/ uggs for women
http://www.adidas-yeezyboost350.us.com/ adidas yeezy
http://www.rayban--glasses.us.com/ ray ban eyeglasses
http://www.new--balance.us.com/ new balance 574
http://www.louboutinredbottoms.us.com/ christian louboutin
http://www.stephen-curry-shoes.us.com/ stephen curry shoes
http://www.mcms.us.com/ mcm handbags
http://www.monclerjacket.org.uk/ moncler coat
http://www.air-max-95.us.com/ air max 95 mens
http://www.asics--shoes.us.com/ asics womens shoes
http://www.pandorauk.us.com/ pandora uk
http://www.coach--bags.us.com/ coach purses
http://www.lacosteshirts.us.com/ lacoste outlet
http://www.pandora--rings.us.com/ Pandora Rings
http://www.birkenstock--sandals.us.com/ birkenstock sale
http://www.monclerjacketmens.us.com/ moncler,moncler jacket
http://www.burberry--scarf.us.com/ burberry outlet
http://www.uggsformen.us.com/ uggs for women
http://www.nike-huaraches.us.com/ nike huarache
http://www.true--religion.us.com/ true religion jeans men
http://www.ferragamoshoess.us.com/ ferragamo shoes men
http://www.jimmychooheels.us.com/ jimmy choo
http://www.skechersuk.co.uk/ skechers
http://www.nike--vapormax.us.com/ nike vapormax
http://www.nike-airmax-2018.us.com/ air max
http://www.adidasnmdrunnerr1.us.com/ yeezy boost 350
http://www.montblancs.us.com/ mont blanc pens
http://www.valentino--shoes.us.com/ valentino shoes
http://www.nikeairmax-97.us.com/ nike air max 97
http://www.yeezyboost350--v2.us.com/ yeezy boost 350
http://www.chromeheartsjewelrys.us.com/ chrome hearts t shirt
http://www.balenciaga--shoes.us.com/ balenciaga
http://www.air-max-270.us.com/ nike air max 270
http://www.airmax-2018.us.com/ nike air max
http://www.mulberrys.org.uk/ mulberry handbags
http://www.mcm--bags.us.com/ mcm
http://www.asicss.us.com/ asics womens running shoes
http://www.james-hardenshoes.us.com/ harden vol 2
http://www.adidas--shoes.co.uk/ adidas
http://www.northface-jacket.us.com/ womens north face jacket
http://www.adidasyeezys.org.uk/ yeezy boost 350
http://www.monclers.uk/ moncler jacket womens
http://www.nikeair-max90.co.uk/ nike air max 2018
http://www.prada--bags.us.com/ prada purse
http://www.ralphlaurenspoloshirts.us.com/ ralph lauren
http://www.northfacejacketoutlets.us.com/ north face vest
http://www.michael-kors-bags.us.com/ michael kors outlet
http://www.pandorajewelryscharms.us.com/ pandora jewelry
http://www.nike--shoes.co.uk/ nike air max 97
http://www.airmax95.co.uk/ nike air max 97
http://www.pandorasjewelry.co.uk/ pandora uk
http://www.burberry-bags.us.com/ burberry
http://www.curry4-shoes.us.com/ curry 4 shoes
http://www.ralphlauren--polo.us.com/ ralph lauren outlet
http://www.hermes--belt.us.com/ hermes
http://www.adidasoriginalsnmd.us.com/ adidas nmd
http://www.goyardbackpack.us.com/ goyard tote
http://www.oakley--sunglassess.us.com/ cheap oakley sunglasses
http://www.michaelkors-handbagss.us.com/ michael kors outlet
http://www.jordan11.co.uk/ air jordan
http://www.jordanretro11-shoes.us.com/ jordan retro
http://www.adidasnmd-womens.us.com/ nmd
http://www.chromehearts-jewelry.us.com/ chrome hearts bracelet
http://www.huaraches.us.com/ nike air huarache
http://www.redbottom--shoes.us.com/ red bottom shoes
http://www.airmax90shoes.us.com/ nike air max 2018
http://www.ray--bansunglassess.us.com/ ray ban glasses
http://www.adidas-superstarshoes.us.com/ adidas
http://www.jordan11spacejams.us.com/ jordan shoes
http://www.swarovskisjewelry.us.com/ swarovski
http://www.pandora-jewelrybracelet.us.com/ pandora rings
http://www.cartier-bracelet.us.com/ cartier glasses
http://www.salomonspeedcross3.us.com/ salomon shoes
http://www.ultra--boost.us.com/ ultra boost
http://www.katespadebags.us.com/ kate spade bags
http://www.nikeairmax270.org.uk/ nike air max 97
http://www.salomon-boots.us.com/ salomon shoes
http://www.pandoras-uk.co.uk/ pandora bracelet
http://www.eccoshoesoutlets.us.com/ ecco shoes
http://www.supreme--clothing.us.com/ supreme shoes
http://www.polo-ralphlauren-outlet.us.com/ ralph lauren polo shirts
http://www.longchampbackpack.us.com/ longchamp bag
http://www.pandora-charmsjewelry.us.com/ pandora earrings
http://www.moncler-coat.us.com/ moncler coat
http://www.pumarihannafenty.us.com/ puma shoes
http://www.truereligion--jeans.us.com/ true religion
http://www.vapormaxs.us.com/ nike air vapormax flyknit
http://www.salvatore-ferragamo.us.com/ salvatore ferragamo shoes
http://www.pandora-jewelrysale.us.com/ pandora jewelry official site
http://www.pandoras-jewelrys.us.com/ pandora jewelry
http://www.nikelebron15.us.com/ lebron shoes
http://www.salomon--shoes.us.com/ Salomon Speedcross 3
http://www.polo-ralph-lauren.org.uk/ ralph lauren polo shirts
http://www.pandorajewelryrings.us.com/ pandora earrings
http://www.uggs--boots.us.com/ ugg slippers
http://www.prada--handbags.us.com/ prada handbags
http://www.adidas-yeezy-shoes.us.com/ Yeezy Shoes
http://www.air-max-90.us.com/ nike shoes
http://www.katespade--outlet.us.com/ kate spade bags
qingyi94님의 댓글
qingyi94 작성일
http://www.eccoshoesoutlets.us.com/ ecco mens shoes
http://www.michael-kors-bags.us.com/ michael kors bags
http://www.christianlouboutinredbottoms.us.com/ christian louboutin
http://www.balenciaga--shoes.us.com/ balenciaga
http://www.pandora-jewelrybracelet.us.com/ pandora,pandora charms
http://www.katespadebags.us.com/ kate spade
http://www.fitflop--shoes.us.com/ fitflop sandals
http://www.airjordan11spacejam.us.com/ air jordan
http://www.mbts.us.com/ mbt
http://www.air-max-95.us.com/ nike air max 95
http://www.rayban--glasses.us.com/ ray ban sunglasses
http://www.stephen-curry-shoes.us.com/ stephen curry shoes
http://www.adidasnmdrunnerr1.us.com/ didas ultra boost
http://www.adidasyeezys.org.uk/ yeezy boost 350
http://www.kevin-durant-shoes.us.com/ kd 10
http://www.celines.us.com/ celine purse
http://www.salvatore-ferragamo.us.com/ salvatore ferragamo
http://www.polo-ralphlauren-outlet.us.com/ ralph lauren polo shirts
http://www.katespadepurses.us.com/ kate spade bags
http://www.longchampbag.us.com/ longchamp le pliage
http://www.coachbags-outlet.us.com/ coach outlet
http://www.pandora-charmsjewelry.us.com/ pandora earrings
http://www.monclers.uk/ moncler sale
http://www.hermesbirkin-handbags.us.com/ Hermes Birkin Bags
http://www.new--balance.us.com/ new balance
http://www.nike-airmax-2018.us.com/ air max 90
http://www.nike--shoes.co.uk/ nike air max 97
http://www.jimmychooheels.us.com/ jimmy choo
http://www.montblancs.us.com/ mont blanc outlet
http://www.pandora--rings.us.com/ Pandora Charms
http://www.fitflop--sandals.us.com/ fitflop sale
http://www.barbourjackets.co.uk/ barbour wax jacket
http://www.vapormaxs.us.com/ vapormax
http://www.birkenstocksandalssale.us.com/ birkenstock sale
http://www.salomonspeedcross3.us.com/ salomon speedcross 3
http://www.pandoraearrings.us.com/ pandora charms
http://www.nikeairmax-90.us.com/ air max 90
http://www.fitflopsshoes.us.com/ fitflops clearance
http://www.skechers--shoes.us.com/ skechers shoes
http://www.coach--bags.us.com/ coach outlet
http://www.nikekdshoes.us.com/ kd 10
http://www.goyardbackpack.us.com/ goyard bag
http://www.burberry-bags.us.com/ burberry
http://www.bvlgaris.us.com/ bvlgari ring
http://www.adidas-superstarshoes.us.com/ adidas superstar mens
http://www.mulberry-handbags.us.com/ mulberry bayswater
http://www.adidasnmd-womens.us.com/ adidas originals nmd
http://www.supreme--clothing.us.com/ supreme jacket
http://www.under-armour-shoes.us.com/ under armour outlet
http://www.nikeairmax-97.us.com/ air max 97 gold
http://www.swarovskis.us.com/ swarovski
http://www.chromehearts-jewelry.us.com/ chrome hearts clothing
http://www.adidasoriginalsnmd.us.com/ adidas nmd r1
http://www.oakley--glasses.us.com/ oakley eyeglasses
http://www.ralphlauren--polo.us.com/ ralph lauren
http://www.pandorasjewelry.co.uk/ pandora rings
http://www.goyardbag.us.com/ goyard tote
http://www.kyrie-irving-shoes.us.com/ kyrie
http://www.pandorauk.us.com/ pandora jewelry
http://www.northface-jacket.us.com/ womens north face jacket
http://www.mcm--bags.us.com/ mcm backpack
http://www.northfacejacketoutlets.us.com/ north face coats
http://www.airmax-2018.us.com/ air max 90
http://www.pandoras-uk.co.uk/ pandora
http://www.longchampbackpack.us.com/ longchamp handbag
http://www.barbours.org.uk/ barbour wax jacket
http://www.chrome--hearts.us.com/ chrome hearts t shirt
http://www.moncler-coat.us.com/ moncler coat
http://www.uggs-forwomen.us.com/ ugg boots
http://www.moncler--jacket.us.com/ moncler jacket mens
http://www.burberrys.org.uk/ burberry handbags
http://www.burberry--scarf.us.com/ burberry
http://www.cartier-bracelet.us.com/ cartier glasses
http://www.monclerjacketwomens.us.com/ moncler
http://www.oakley--sunglassess.us.com/ cheap oakley sunglasses
http://www.jordan11spacejams.us.com/ jordan retro 12
http://www.curry4-shoes.us.com/ under armour stephen curry
http://www.pumarihannafenty.us.com/ rihanna puma shoes
http://www.swarovskisjewelry.us.com/ swarovski
http://www.adidas-ultraboost.us.com/ adidas ultra boost
http://www.adidasoriginalsultraboost.us.com/ ultra boost
http://www.ugg--slippers.us.com/ ugg
http://www.kyrie-4.us.com/ kyire 4
http://www.mcms.us.com/ mcm bags
http://www.adidas-yeezy-shoes.us.com/ Yeezy Boost 350 V2
http://www.nikeairmax270.org.uk/ nike air max 270
http://www.uggsformen.us.com/ uggs for women
http://www.huaraches.us.com/ huarache shoes
http://www.katespade--outlet.us.com/ kate spade handbags
http://www.pandora-jewelrysale.us.com/ pandora charms
http://www.lacosteshirts.us.com/ lacoste sale
http://www.nike--vapormax.us.com/ nike air vapormax flyknit
http://www.yeezyboost350shoes.us.com/ yeezy boost 350
http://www.james-hardenshoes.us.com/ james harden shoes
http://www.ed-hardys.us.com/ ed hardy
http://www.ray--ban.us.com/ ray ban glasses
http://www.birkenstock--sandals.us.com/ birkenstock sandals
http://www.kd10-shoes.us.com/ kd 10
http://www.supremeshirt.us.com/ supreme shirt
http://www.balenciagas-sneakers.us.com/ balenciaga shoes
http://www.ferragamoshoess.us.com/ ferragamo shoes
http://www.ralphlaurenspoloshirts.us.com/ polo ralph lauren
http://www.truereligion--jeans.us.com/ true religion
http://www.adidasyeezy-350.us.com/ yeezy boost 350
http://www.redbottom--shoes.us.com/ christian louboutin shoes
http://www.redbottoms-louboutin.us.com/ louboutin
http://www.monclerjacketmens.us.com/ moncler,moncler jacket
http://www.ultra--boost.us.com/ ultra boost
http://www.nikeairmax97.co.uk/ nike air max
http://www.salomonshoes.co.uk/ salomon skis
http://www.skechersuk.co.uk/ skechers for men
http://www.adidas-yeezyboost350.us.com/ yeezy shoes
http://www.air-max-97.us.com/ nike air max 97
http://www.salomon--shoes.us.com/ Salomon xa pro 3d
http://www.airmax95.co.uk/ nike air max 95
http://www.air-max-90.us.com/ nike air max
http://www.jordan11.co.uk/ jordan 11
http://www.adidas--shoes.co.uk/ adidas boost
http://www.nikeair-max.co.uk/ nike air max 270
http://www.nikeairmax-95.us.com/ air max 95
http://www.pandorajewelryrings.us.com/ pandora charms
http://www.skecherss.us.com/ skechers boots
http://www.pandoras-jewelrys.us.com/ pandora rings
http://www.jordan--11.us.com/ jordan 11
http://www.salomon-boots.us.com/ salomon xa pro 3d
http://www.nike-huaraches.us.com/ nike huarache
http://www.monclerjacket.org.uk/ moncler jacket
http://www.nike-airmax270.us.com/ air max 270
http://www.yeezyboost350--v2.us.com/ yeezy boost 350
http://www.ray--bansunglassess.us.com/ ray ban sunglasses
http://www.prada--handbags.us.com/ prada
http://www.jordanretro11-shoes.us.com/ jordan 11
http://www.nikeairvapormaxflyknit.us.com/ vapormax
http://www.asicss.us.com/ asics
http://www.hermes--belt.us.com/ hermes belt
http://www.fitflops-sale.us.com/ fitflop shoes
http://www.airmax270.co.uk/ nike vapormax
http://www.chromeheartsjewelrys.us.com/ chrome hearts t shirt
http://www.uggs--boots.us.com/ ugg
http://www.adidasnmds.co.uk/ adidas nmd r1
http://www.asics--shoes.us.com/ asics shoes
http://www.valentino--shoes.us.com/ valentino sandals
http://www.jordans11shoes.us.com/ jordan shoes
http://www.lebron15-shoes.us.com/ lebron 14
http://www.nikeair-max90.co.uk/ nike air max
http://www.mulberrys.org.uk/ mulberry purse
http://www.air-max-270.us.com/ nike air max 270 men
http://www.michaelkors-handbagss.us.com/ michael kors purse
http://www.louboutinredbottoms.us.com/ louboutin
http://www.airmax90shoes.us.com/ nike air max
http://www.pandorajewelryscharms.us.com/ pandora jewelry official site
http://www.true--religion.us.com/ true religion jeans for women
http://www.polo-ralph-lauren.org.uk/ ralph lauren shirts
http://www.nikelebron15.us.com/ nike lebron
http://www.prada--bags.us.com/ prada wallet
http://www.rayban-glasses.us.com/ ray ban sunglasses
http://www.pandora--jewelrys.us.com/ pandora jewelry
http://www.yeezyboost350v2.co.uk/ yeezy boost 350
xishang49님의 댓글
xishang49 작성일
http://www.truereligion--jeans.us.com/ true religion hoodie
http://www.polo-ralph-lauren.org.uk/ ralph lauren polo shirts
http://www.nikeairmax-95.us.com/ nike air max 95
http://www.pumarihannafenty.us.com/ puma shoes
http://www.yeezyboost350v2.co.uk/ yeezy
http://www.curry4-shoes.us.com/ curry 4 shoes
http://www.under-armour-shoes.us.com/ under armour
http://www.huaraches.us.com/ nike air huarache
http://www.nike-huaraches.us.com/ huarache shoes
http://www.airmax-2018.us.com/ nike air max
http://www.mulberry-handbags.us.com/ mulberry
http://www.nike--shoes.co.uk/ nike outlet
http://www.louboutinredbottoms.us.com/ red bottoms
http://www.kyrie-4.us.com/ kyire 4
http://www.ray--bansunglassess.us.com/ ray ban
http://www.burberry-bags.us.com/ burberry
http://www.eccoshoesoutlets.us.com/ ecco mens shoes
http://www.supremeshirt.us.com/ supreme shirt
http://www.new--balance.us.com/ new balance
http://www.pandorajewelryscharms.us.com/ pandora jewelry
http://www.redbottoms-louboutin.us.com/ christian louboutin
http://www.oakley--glasses.us.com/ oakley prescription sunglasses
http://www.goyardbackpack.us.com/ goyard wallet
http://www.balenciagas-sneakers.us.com/ balenciaga
http://www.adidasnmds.co.uk/ adidas nmd womens
http://www.cartier-bracelet.us.com/ cartier love ring
http://www.pandora--jewelrys.us.com/ pandora rings
http://www.ed-hardys.us.com/ ed hardy jeans
http://www.vapormaxs.us.com/ nike air vapormax
http://www.ultra--boost.us.com/ adidas ultra boost
http://www.nikekdshoes.us.com/ kd shoes
http://www.jordans11shoes.us.com/ jordan shoes
http://www.moncler-coat.us.com/ moncler coat
http://www.nike-airmax270.us.com/ nike air max
http://www.pandora--rings.us.com/ Pandora
http://www.uggs--boots.us.com/ uggs for women
http://www.longchampbackpack.us.com/ longchamp handbag
http://www.pandorasjewelry.co.uk/ pandora charm
http://www.nikeairmax-97.us.com/ air max 97
http://www.balenciaga--shoes.us.com/ balenciaga women
http://www.jordan11.co.uk/ jordan retro 11
http://www.prada--handbags.us.com/ prada bags
http://www.nike-airmax-2018.us.com/ nike air max 2018
http://www.airmax270.co.uk/ nike vapormax
http://www.ferragamoshoess.us.com/ salvatore ferragamo shoes
http://www.valentino--shoes.us.com/ valentino
http://www.birkenstocksandalssale.us.com/ birkenstock sale
http://www.pandorauk.us.com/ pandora rings
http://www.nike--vapormax.us.com/ nike air vapormax flyknit
http://www.northface-jacket.us.com/ north face coats
http://www.salomonspeedcross3.us.com/ salomon xa pro 3d
http://www.monclerjacket.org.uk/ moncler jacket womens
http://www.adidasoriginalsultraboost.us.com/ adidas ultra boost
http://www.michael-kors-bags.us.com/ michael kors purse
http://www.yeezyboost350shoes.us.com/ yeezy
http://www.monclers.uk/ moncler coat
http://www.chromeheartsjewelrys.us.com/ chrome hearts jewelry
http://www.mulberrys.org.uk/ mulberry sale
http://www.monclerjacketmens.us.com/ moncler jacket womens
http://www.salvatore-ferragamo.us.com/ salvatore
http://www.kd10-shoes.us.com/ kevin durant shoes
http://www.swarovskis.us.com/ swarovski rings
http://www.asicss.us.com/ asics
http://www.mbts.us.com/ mbt
http://www.montblancs.us.com/ mont blanc outlet
http://www.rayban-glasses.us.com/ ray ban glasses
http://www.coach--bags.us.com/ coach outlet
http://www.skechers--shoes.us.com/ skechers boots
http://www.christianlouboutinredbottoms.us.com/ christian louboutin
http://www.supreme--clothing.us.com/ supreme clothing
http://www.coachbags-outlet.us.com/ coach
http://www.airjordan11spacejam.us.com/ air jordan
http://www.barbours.org.uk/ barbour outlet
http://www.air-max-90.us.com/ nike shoes
http://www.pandorajewelryrings.us.com/ pandora charms
http://www.longchampbag.us.com/ longchamp
http://www.rayban--glasses.us.com/ ray ban glasses
http://www.ugg--slippers.us.com/ ugg slippers
http://www.nikeairmax97.co.uk/ nike air max 97
http://www.pandora-jewelrysale.us.com/ pandora charms
http://www.nikeairmax-90.us.com/ nike air max 90
http://www.monclerjacketwomens.us.com/ moncler jacket womens
http://www.fitflops-sale.us.com/ fitflops clearance
http://www.adidas-ultraboost.us.com/ yeezy boost
http://www.nikeairmax270.org.uk/ nike air max 90
http://www.redbottom--shoes.us.com/ christian louboutin shoes
http://www.skecherss.us.com/ skechers boots
http://www.fitflopsshoes.us.com/ fitflop sandals
http://www.skechersuk.co.uk/ skechers outlet
http://www.yeezyboost350--v2.us.com/ yeezy boost 350 v2
http://www.nikeairvapormaxflyknit.us.com/ nike air force 1
http://www.adidas-yeezy-shoes.us.com/ Yeezy
http://www.salomonshoes.co.uk/ salomon xa pro 3d
http://www.barbourjackets.co.uk/ barbour outlet
http://www.adidasnmdrunnerr1.us.com/ adidas nmd r1
http://www.nikeair-max90.co.uk/ nike vapormax
http://www.mcm--bags.us.com/ mcm handbags
http://www.kevin-durant-shoes.us.com/ nike kd
http://www.burberry--scarf.us.com/ burberry
http://www.mcms.us.com/ mcm backpack
http://www.adidas-yeezyboost350.us.com/ yeezy shoes
http://www.chrome--hearts.us.com/ chrome hearts necklace
http://www.polo-ralphlauren-outlet.us.com/ polo ralph lauren outlet
http://www.stephen-curry-shoes.us.com/ curry 4
http://www.prada--bags.us.com/ prada wallet
http://www.air-max-95.us.com/ air max 95 mens
http://www.true--religion.us.com/ true religion jeans
http://www.salomon-boots.us.com/ salomon speedcross 3
http://www.katespade--outlet.us.com/ kate spade outlet
http://www.air-max-270.us.com/ nike air max 270 men
http://www.oakley--sunglassess.us.com/ oakley sunglasses
http://www.katespadepurses.us.com/ kate spade outlet
http://www.adidasoriginalsnmd.us.com/ adidas nmd r1
http://www.asics--shoes.us.com/ asics shoes
http://www.uggsformen.us.com/ ugg boots
http://www.hermesbirkin-handbags.us.com/ Hermes Belts
http://www.lebron15-shoes.us.com/ lebron james shoes
http://www.michaelkors-handbagss.us.com/ michael kors bags
http://www.james-hardenshoes.us.com/ harden vol 2
http://www.jordanretro11-shoes.us.com/ jordan retro
http://www.pandora-jewelrybracelet.us.com/ pandora rings
http://www.adidasyeezy-350.us.com/ yeezy shoes
http://www.adidas-superstarshoes.us.com/ adidas originals superstar
http://www.hermes--belt.us.com/ hermes belt
http://www.pandoras-jewelrys.us.com/ pandora charms
http://www.ralphlaurenspoloshirts.us.com/ ralph lauren polo shirts
http://www.airmax95.co.uk/ air max 95
http://www.jimmychooheels.us.com/ jimmy choo trainers
http://www.adidasyeezys.org.uk/ yeezy boost 350
http://www.goyardbag.us.com/ goyard tote
http://www.ralphlauren--polo.us.com/ ralph lauren
http://www.pandora-charmsjewelry.us.com/ pandora bracelet
http://www.fitflop--shoes.us.com/ fitflop shoes
http://www.lacosteshirts.us.com/ lacoste shoes
http://www.adidas--shoes.co.uk/ adidas boost
http://www.ray--ban.us.com/ ray ban sunglasses
http://www.air-max-97.us.com/ air max 97
http://www.pandoras-uk.co.uk/ pandora charms
http://www.pandoraearrings.us.com/ pandora charms
http://www.fitflop--sandals.us.com/ fitflops uk
http://www.birkenstock--sandals.us.com/ birkenstock sale
http://www.uggs-forwomen.us.com/ ugg boots
http://www.salomon--shoes.us.com/ Salomon Boots
http://www.swarovskisjewelry.us.com/ swarovski jewelry
http://www.katespadebags.us.com/ kate spade handbags
http://www.bvlgaris.us.com/ bvlgari handbags
http://www.adidasnmd-womens.us.com/ nmd
http://www.northfacejacketoutlets.us.com/ north face outlet
http://www.nikeair-max.co.uk/ nike air max 270
http://www.nikelebron15.us.com/ lebron 15
http://www.airmax90shoes.us.com/ nike vapormax
http://www.jordan11spacejams.us.com/ jordan retro 12
http://www.chromehearts-jewelry.us.com/ chrome hearts
http://www.kyrie-irving-shoes.us.com/ kyrie
http://www.celines.us.com/ celine wallet
http://www.moncler--jacket.us.com/ moncler coat
http://www.burberrys.org.uk/ burberry scarf
http://www.jordan--11.us.com/ jordan
yuanbo37님의 댓글
yuanbo37 작성일
http://www.monclerjacket.org.uk/ moncler coat
http://www.nikelebron15.us.com/ lebron shoes
http://www.nikeairmax-97.us.com/ nike air max 97
http://www.fitflopsshoes.us.com/ fitflop shoes
http://www.ralphlauren--polo.us.com/ ralph lauren
http://www.nike-airmax-2018.us.com/ nike air max
http://www.jimmychooheels.us.com/ jimmy choo
http://www.air-max-97.us.com/ nike air max 97
http://www.ed-hardys.us.com/ ed hardy shirt
http://www.barbourjackets.co.uk/ barbour wax jacket
http://www.mcm--bags.us.com/ mcm backpack
http://www.adidasyeezys.org.uk/ adidas yeezy
http://www.burberry-bags.us.com/ burberry
http://www.swarovskis.us.com/ swarovski rings
http://www.cartier-bracelet.us.com/ cartier sunglasses
http://www.pandora-charmsjewelry.us.com/ pandora
http://www.ferragamoshoess.us.com/ ferragamo shoes
http://www.mbts.us.com/ mbt womens shoes
http://www.nike--vapormax.us.com/ vapormax
http://www.airmax270.co.uk/ nike air max 270
http://www.adidasoriginalsultraboost.us.com/ ultra boost uncaged
http://www.ray--bansunglassess.us.com/ ray ban glasses
http://www.fitflop--shoes.us.com/ fitflop sale
http://www.redbottom--shoes.us.com/ red bottoms
http://www.ralphlaurenspoloshirts.us.com/ ralph lauren outlet
http://www.adidas--shoes.co.uk/ adidas outlet
http://www.yeezyboost350shoes.us.com/ yeezy shoes
http://www.rayban-glasses.us.com/ ray ban
http://www.nikeair-max90.co.uk/ nike air max 2018
http://www.adidasoriginalsnmd.us.com/ nmd
http://www.airmax-2018.us.com/ nike air max
http://www.katespadepurses.us.com/ kate spade handbags
http://www.ray--ban.us.com/ ray ban
http://www.balenciaga--shoes.us.com/ balenciaga sneakers
http://www.uggsformen.us.com/ ugg,ugg slippers
http://www.yeezyboost350v2.co.uk/ yeezy shoes
http://www.burberrys.org.uk/ burberry scarf
http://www.katespade--outlet.us.com/ kate spade
http://www.uggs--boots.us.com/ uggs on sale
http://www.nikeairmax-95.us.com/ nike air max 95 mens
http://www.oakley--sunglassess.us.com/ oakley
http://www.kyrie-irving-shoes.us.com/ nike kyrie
http://www.skecherss.us.com/ skechers outlet
http://www.moncler-coat.us.com/ moncler
http://www.redbottoms-louboutin.us.com/ louboutin
http://www.barbours.org.uk/ barbour coats
http://www.air-max-90.us.com/ air max 90
http://www.new--balance.us.com/ new balance running shoes women
http://www.adidasnmds.co.uk/ adidas nmd womens
http://www.rayban--glasses.us.com/ ray ban glasses
http://www.adidas-yeezyboost350.us.com/ yeezy shoes
http://www.adidasyeezy-350.us.com/ yeezy
http://www.chromehearts-jewelry.us.com/ chrome hearts pendant
http://www.nikeairmax-90.us.com/ nike vapormax
http://www.pandorajewelryscharms.us.com/ pandora Charms
http://www.pandorasjewelry.co.uk/ pandora rings
http://www.birkenstocksandalssale.us.com/ birkenstock sandals
http://www.adidasnmd-womens.us.com/ adidas nmd womens
http://www.skechersuk.co.uk/ skechers
http://www.goyardbackpack.us.com/ goyard tote
http://www.salvatore-ferragamo.us.com/ ferragamo
http://www.vapormaxs.us.com/ nike air vapormax flyknit
http://www.james-hardenshoes.us.com/ james harden
http://www.truereligion--jeans.us.com/ true religion jeans
http://www.balenciagas-sneakers.us.com/ balenciaga bags
http://www.nikekdshoes.us.com/ kd 9
http://www.pumarihannafenty.us.com/ puma fenty
http://www.asics--shoes.us.com/ asics mens running shoes
http://www.jordanretro11-shoes.us.com/ jordan retro
http://www.pandorajewelryrings.us.com/ pandora bracelet
http://www.adidas-ultraboost.us.com/ adidas ultra boost
http://www.mulberrys.org.uk/ mulberry sale
http://www.jordans11shoes.us.com/ jordan shoes
http://www.coach--bags.us.com/ coach purses
http://www.true--religion.us.com/ true religion outlet
http://www.mcms.us.com/ mcm
http://www.salomon-boots.us.com/ salomon speedcross 3
http://www.supremeshirt.us.com/ supreme clothing
http://www.chrome--hearts.us.com/ chrome hearts
http://www.air-max-95.us.com/ air max 95
http://www.celines.us.com/ celine purse
http://www.jordan11spacejams.us.com/ jordan retro 12
http://www.nikeairmax270.org.uk/ nike air max 95
http://www.moncler--jacket.us.com/ moncler jacket mens
http://www.kevin-durant-shoes.us.com/ kd shoes
http://www.michaelkors-handbagss.us.com/ michael kors outlet
http://www.yeezyboost350--v2.us.com/ yeezy shoes
http://www.nikeairmax97.co.uk/ air max 97
http://www.coachbags-outlet.us.com/ coach
http://www.adidas-yeezy-shoes.us.com/ Yeezy Boost 350
http://www.eccoshoesoutlets.us.com/ ecco boots
http://www.pandora-jewelrybracelet.us.com/ pandora rings
http://www.ugg--slippers.us.com/ uggs for men
http://www.pandora-jewelrysale.us.com/ pandora jewelry
http://www.airjordan11spacejam.us.com/ air jordan 11 space jam
http://www.monclerjacketmens.us.com/ moncler jacket womens
http://www.jordan11.co.uk/ jordan shoes
http://www.lebron15-shoes.us.com/ lebron 15
http://www.nike--shoes.co.uk/ nike shoes
http://www.louboutinredbottoms.us.com/ louboutin shoes
http://www.valentino--shoes.us.com/ valentino
http://www.bvlgaris.us.com/ bvlgari sunglasses
http://www.oakley--glasses.us.com/ oakley sunglasses
http://www.under-armour-shoes.us.com/ under armour outlet
http://www.birkenstock--sandals.us.com/ birkenstock
http://www.hermesbirkin-handbags.us.com/ Hermes Belts
http://www.lacosteshirts.us.com/ lacoste shoes
http://www.mulberry-handbags.us.com/ mulberry handbags
http://www.fitflops-sale.us.com/ fitflops clearance
http://www.salomon--shoes.us.com/ Salomon Shoes
http://www.jordan--11.us.com/ jordan 11
http://www.airmax95.co.uk/ nike air max 95 mens
http://www.uggs-forwomen.us.com/ uggs for women
http://www.pandoraearrings.us.com/ pandora rings
http://www.ultra--boost.us.com/ adidas ultra boost uncaged
http://www.huaraches.us.com/ nike air huarache
http://www.hermes--belt.us.com/ hermes belt
http://www.nike-huaraches.us.com/ huaraches
http://www.supreme--clothing.us.com/ supreme jacket
http://www.burberry--scarf.us.com/ burberry
http://www.nike-airmax270.us.com/ nike air max 270
http://www.polo-ralphlauren-outlet.us.com/ polo
http://www.asicss.us.com/ asics womens running shoes
http://www.swarovskisjewelry.us.com/ swarovski bracelet
http://www.stephen-curry-shoes.us.com/ stephen curry
http://www.northfacejacketoutlets.us.com/ north face coats
http://www.pandora--jewelrys.us.com/ pandora
http://www.longchampbackpack.us.com/ longchamp backpack
http://www.pandoras-uk.co.uk/ pandora jewelry
http://www.kd10-shoes.us.com/ kevin durant shoes
http://www.monclerjacketwomens.us.com/ moncler
http://www.prada--handbags.us.com/ prada wallet
http://www.polo-ralph-lauren.org.uk/ ralph lauren shirts
http://www.katespadebags.us.com/ kate spade handbags
http://www.pandora--rings.us.com/ Pandora Bracelet
http://www.northface-jacket.us.com/ womens north face jacket
http://www.skechers--shoes.us.com/ skechers boots
http://www.curry4-shoes.us.com/ under armour stephen curry
http://www.adidasnmdrunnerr1.us.com/ yeezy boost 350
http://www.chromeheartsjewelrys.us.com/ chrome hearts t shirt
http://www.michael-kors-bags.us.com/ michael kors outlet
http://www.fitflop--sandals.us.com/ fitflop sale
http://www.prada--bags.us.com/ prada
http://www.goyardbag.us.com/ goyard bag
http://www.salomonshoes.co.uk/ salomon skis
http://www.monclers.uk/ moncler coat
http://www.nikeair-max.co.uk/ nike shoes
http://www.longchampbag.us.com/ longchamp backpack
http://www.kyrie-4.us.com/ kyire 4
http://www.adidas-superstarshoes.us.com/ adidas originals superstar
http://www.airmax90shoes.us.com/ nike air max
http://www.pandorauk.us.com/ pandora jewelry
http://www.nikeairvapormaxflyknit.us.com/ nike air max 90
http://www.montblancs.us.com/ mont blanc pens
http://www.salomonspeedcross3.us.com/ salomon xa pro 3d
http://www.pandoras-jewelrys.us.com/ pandora earrings
http://www.christianlouboutinredbottoms.us.com/ louboutin
http://www.huaraches.us.com/ nike air huarache
yitao69님의 댓글
yitao69 작성일
http://www.katespades.ca/ kate spade
http://www.birkenstock-sandals.ca/ birkenstock canada
http://www.salomonshoes.ca/ salomon speedcross 4
http://www.airmax90.fr/ nike air max 90
http://www.balenciagas.ca/ balenciaga canada
http://www.adidasnmds.us/ adidas originals nmd
http://www.bracelet-pandora.fr/ pandora
http://www.chaussure-yeezy.fr/ yeezy boost 350 v2
http://www.skechers-shoes.ca/ skechers
http://www.pandora--jewelry.co.uk/ pandora rings
http://www.nikebasketballshoes.us/ kyrie irving shoes
http://www.airjordan11.fr/ air jordan 11 retro
http://www.monclers.us.com/ moncler coat
http://www.nikeoffwhite.us.com/ nike off white
http://www.chaussuresskechers.fr/ chaussures skechers
http://www.yeezy-750.us/ yeezy shoes
http://www.nike-canada.ca/ nike shoes
http://www.giuseppezanottisneakers.us/ giuseppe
http://www.uggsforwomen.us/ ugg slippers
http://www.red-bottoms.ca/ louboutin
http://www.goldengoosesneakerssale.us/ golden goose outlet
http://www.monclers.ca/ moncler jacket
http://www.jordan-retro11.us.com/ jordan shoes
http://www.christianlouboutins.fr/ louboutin femme
http://www.louboutin-shoesuk.co.uk/ christian louboutin uk
http://www.monclers.fr/ moncler doudoune
http://www.goldengoosesale.us/ golden goose outlet
http://www.ugg-pascher.fr/ ugg pas cher
http://www.ultra-boost.ca/ adidas boost
http://www.nike--trainers.org.uk/ nike shoes
http://www.nike-airmax.ca/ nike air max 270
http://www.nmd.us.org/ adidas nmd
http://www.curry-5shoes.us/ steph curry
http://www.jordan11shoes.us.com/ jordan 11
http://www.skechers-shoe.us.com/ skechers
http://www.adidaschaussure.fr/ chaussure adidas
http://www.adidaszxflux.us/ adidas zx flux
http://www.pandorajewelrycharms.ca/ pandora charms
http://www.jordanretro11.in.net/ air jordan
http://www.yeezyshoes.ca/ yeezy
http://www.jordan-11.fr/ jordan,jordan 13
http://www.adidasboostoutlet.us/ adidas outlet
http://www.air-max.us/ nike air max 90
http://www.salomonboots.co.uk/ salomon xa pro 3d
http://www.golden-goosesneakers.us.com/ golden goose
http://www.kate-spadepurses.us/ kate spade
http://www.ultraboost-uncaged.us/ ultra boost
http://www.fjallravenkanken-backpack.us/ fjallraven
http://www.bijoux-pandora.fr/ bracelet pandora
http://www.mizunos.us/ mizuno
http://www.nikeairmax-2019.us.com/ air max 2019
http://www.red-bottoms.org.uk/ red bottoms
http://www.goyards.ca/ goyard handbags
http://www.pandora-bracelet.fr/ bijoux pandora
http://www.bijouxpandoras.fr/ pandora
http://www.nikeairmax.fr/ air max
http://www.goyard.in.net/ goyard tote
http://www.pandora--jewelry.us.org/ pandora
http://www.moncler-uk.co.uk/ moncler jacket
http://www.chaussurelouboutinpascher.fr/ chaussure louboutin
http://www.nmds.ca/ adidas nmd
http://www.adidaseqtsupportadv.us/ adidas originals eqt
http://www.fitflop-shoes.ca/ fitflop sandals
http://www.redbottomslouboutinshoes.us.com/ red bottom shoes
http://www.adidasshoes-outlet.us/ adidas superstar
http://www.skechers.in.net/ skechers shoes
http://www.pandoracanadacharms.ca/ pandora rings
http://www.fila-shoes.us/ fila shoes
http://www.yeezyboost-350v2.fr/ yeezy boost
http://www.monclerjacket.us/ moncler jacket
http://www.longchampbags.ca/ longchamp
http://www.kd11shoes.us/ kd 11
http://www.jordan11.ca/ jordan retro 11
http://www.birkenstock.com.co/ birkenstock outlet
http://www.yeezy.in.net/ yeezy boost 350
http://www.philipppleinoutlet.us/ philipp plein t shirt
http://www.nike-basketballshoes.us.com/ kd 11
http://www.adidas--trainers.org.uk/ adidas uk
http://www.yeezys.fr/ adidas yeezy
http://www.doudoune-moncler.fr/ moncler doudoune
http://www.adidastrainers-uk.co.uk/ adidas shoes
http://www.philipppleins.us/ philipp plein
http://www.nike-vapormax.ca/ nike air vapormax
http://www.chaussuresalomon.fr/ salomon
http://www.pandoraukrings.co.uk/ pandora uk
http://www.pandoras.in.net/ pandora charm
http://www.mizuno-shoes.us/ mizuno
http://www.zxflux.us/ adidas flux
http://www.redbottom-shoes.co.uk/ louboutin heels
http://www.newjordans.in.net/ jordan 11
http://www.redbottoms-shoes.us.org/ red bottoms
http://www.balenciagas.co.uk/ balenciagas
http://www.lebron16-shoes.us/ lebron 16
http://www.giuseppezanottis.us/ isabel marant
http://www.balenciaga.us.org/ balenciaga bag
http://www.jordan--shoes.us.com/ jordan retro
http://www.adidasyeezyboost.fr/ yeezy boost 350 v2
http://www.katespade-bags.us/ kate spade outlet
http://www.fjallravenkankens.us/ fjallraven
http://www.chaussure-adidas.fr/ adidas chaussure
http://www.red-bottoms.us.org/ christian louboutin
http://www.christianlouboutins.ca/ christian louboutin
http://www.jordan-11.co.uk/ jordan 11
http://www.yeezy-500.us/ yeezy shoes
http://www.nikeairmax90.ca/ air max 97
http://www.salomon.us.org/ salomon xa pro 3d
http://www.pandorajewelrycharms.org.uk/ pandora uk
http://www.yeezy--shoes.co.uk/ yeezy
http://www.adidascanada-shoes.ca/ adidas canada
http://www.nikeuktrainers.co.uk/ nike trainers
http://www.goyard.org.uk/ goyard wallet,goyard london
http://www.salomon-chaussures.fr/ salomon speedcross
http://www.pandora-jewelrys.ca/ pandora jewelry
http://www.adidas-nmd.fr/ Adidas Yeezy
http://www.adidaseqt.us.org/ adidas eqt
http://www.lebron-16shoes.us/ lebron james shoes
http://www.nikeoffwhiteshoes.us/ off white
http://www.airmax-2019.us.com/ air max 270
http://www.long-champs.us.com/ longchamp bag
http://www.uggboots-outlet.us/ ugg
http://www.kd11-shoes.us/ kevin durant shoes
http://www.nikeairmax270.ca/ air max 270
http://www.adidas--yeezy.co.uk/ yeezy
http://www.goyardhandbags.us/ goyard wallet
http://www.yeezy-950.us/ yeezy boost 950
http://www.katespades.co.uk/ kate spade outlet
http://www.bottesugg.fr/ ugg bottes
http://www.pandoraukcharms.org.uk/ pandora rings
http://www.filas.us.org/ fila shoes
http://www.vans--shoes.us.com/ vans
http://www.uggslippers.ca/ ugg canada
http://www.adidasyeezyshoes.co.uk/ yeezy
http://www.uggboots-uk.co.uk/ ugg uk
http://www.jordan11.us.com/ new jordans
lingshuang61님의 댓글
lingshuang61 작성일
http://www.pandoras.in.net/ pandora jewelry
http://www.balenciagas.ca/ balenciaga bag
http://www.nike-airmax.ca/ nike air max 90
http://www.nmd.us.org/ adidas originals nmd
http://www.ugg-pascher.fr/ ugg bottes
http://www.skechers-shoe.us.com/ skechers outlet
http://www.christianlouboutins.ca/ louboutin
http://www.giuseppezanottis.us/ giuseppe zanotti
http://www.lebron-16shoes.us/ lebron 15
http://www.long-champs.us.com/ longchamp bag
http://www.jordan11.us.com/ new jordans
http://www.salomon.us.org/ salomon
http://www.salomon-chaussures.fr/ salomon speedcross
http://www.pandoracanadacharms.ca/ pandora canada
http://www.philipppleins.us/ philipp plein t shirt
http://www.goyard.in.net/ goyard
http://www.curry-5shoes.us/ curry
http://www.mizuno-shoes.us/ mizuno wave rider
http://www.jordan-11.co.uk/ jordan 12
http://www.redbottomslouboutinshoes.us.com/ red bottoms
http://www.adidaseqtsupportadv.us/ adidas eqt support adv
http://www.salomonshoes.ca/ salomon
http://www.red-bottoms.org.uk/ louboutin heels
http://www.yeezy-950.us/ yeezy 750
http://www.goyard.org.uk/ goyard bag
http://www.vans--shoes.us.com/ vans
http://www.monclers.fr/ moncler doudoune
http://www.red-bottoms.ca/ louboutin
http://www.adidascanada-shoes.ca/ adidas superstar
http://www.adidasnmds.us/ nmd
http://www.uggboots-outlet.us/ ugg
http://www.adidas--yeezy.co.uk/ yeezy 350
http://www.bracelet-pandora.fr/ pandora
http://www.ultra-boost.ca/ ultra boost uncaged
http://www.airjordan11.fr/ jordan 13
http://www.uggslippers.ca/ ugg canada
http://www.chaussuresalomon.fr/ salomon speedcross
http://www.golden-goosesneakers.us.com/ golden goose sneakers
http://www.redbottom-shoes.co.uk/ louboutin
http://www.nike--trainers.org.uk/ nike air max
http://www.airmax-2019.us.com/ nike air max 2019
http://www.fila-shoes.us/ fila shoes womens
http://www.chaussure-adidas.fr/ adidas superstar
http://www.yeezy--shoes.co.uk/ yeezy
http://www.adidasboostoutlet.us/ adidas shoes for men
http://www.yeezy.in.net/ yeezy boost 350 v2
http://www.chaussure-yeezy.fr/ yeezy
http://www.yeezyshoes.ca/ yeezy
http://www.adidas--trainers.org.uk/ adidas outlet
http://www.nikeairmax90.ca/ air max 97
http://www.goldengoosesneakerssale.us/ golden goose outlet
http://www.nmds.ca/ adidas shoes
http://www.goyardhandbags.us/ goyard bag
http://www.jordan-retro11.us.com/ jordan 11
http://www.filas.us.org/ fila shoes womens
http://www.birkenstock-sandals.ca/ birkenstock
http://www.skechers-shoes.ca/ skechers canada
http://www.adidaseqt.us.org/ adidas originals eqt
http://www.ultraboost-uncaged.us/ ultra boost
http://www.nikebasketballshoes.us/ steph curry shoes
http://www.christianlouboutins.fr/ louboutin
http://www.nikeoffwhiteshoes.us/ off white shoes
http://www.bijouxpandoras.fr/ bague pandora
http://www.moncler-uk.co.uk/ moncler
http://www.nike-vapormax.ca/ nike air max
http://www.monclers.us.com/ moncler sale
http://www.fjallravenkankens.us/ fjallraven backpack
http://www.pandorajewelrycharms.org.uk/ pandora uk
http://www.chaussuresskechers.fr/ skechers femme
http://www.pandorajewelrycharms.ca/ pandora
http://www.chaussurelouboutinpascher.fr/ louboutin
http://www.jordan11.ca/ jordan 11
http://www.giuseppezanottisneakers.us/ isabel marant sneakers
http://www.kate-spadepurses.us/ kate spade purses
http://www.adidasyeezyboost.fr/ yeezy boost 350
http://www.pandora--jewelry.us.org/ pandora rings
http://www.monclers.ca/ moncler
http://www.katespades.co.uk/ kate spade handbags
http://www.pandoraukcharms.org.uk/ pandora uk
http://www.balenciaga.us.org/ balenciaga bag
http://www.yeezy-750.us/ yeezy boost 350
http://www.pandoraukrings.co.uk/ pandora
http://www.nikeairmax-2019.us.com/ nike off white
http://www.zxflux.us/ zx flux
http://www.yeezy-500.us/ yeezy shoes
http://www.airmax90.fr/ nike air max 95
http://www.balenciagas.co.uk/ balenciaga trainers
http://www.nike-basketballshoes.us.com/ basketball shoes
http://www.salomonboots.co.uk/ salomon
http://www.redbottoms-shoes.us.org/ christian louboutin
http://www.monclerjacket.us/ moncler sale
http://www.katespades.ca/ kate spade
http://www.bottesugg.fr/ ugg pas cher
http://www.jordanretro11.in.net/ air jordan
http://www.birkenstock.com.co/ birkenstock
http://www.philipppleinoutlet.us/ philipp plein
http://www.mizunos.us/ mizuno running shoes
http://www.lebron16-shoes.us/ lebron 16
http://www.adidasyeezyshoes.co.uk/ yeezy boost
http://www.longchampbags.ca/ longchamp canada
http://www.red-bottoms.us.org/ red bottom shoes
http://www.yeezyboost-350v2.fr/ yeezy boost 350
http://www.louboutin-shoesuk.co.uk/ louboutin
http://www.nikeoffwhite.us.com/ off white
http://www.fjallravenkanken-backpack.us/ fjallraven backpack
http://www.jordan--shoes.us.com/ jordan shoes
http://www.nikeairmax270.ca/ air max 270
http://www.pandora-bracelet.fr/ pandora
http://www.nike-canada.ca/ nike outlet
http://www.jordan-11.fr/ jordan 11
http://www.uggboots-uk.co.uk/ ugg
http://www.nikeuktrainers.co.uk/ nike air max 95
http://www.adidas-nmd.fr/ Adidas Nmd Femme
http://www.goldengoosesale.us/ golden goose outlet
http://www.jordan11shoes.us.com/ jordan 11 space jam
http://www.adidasshoes-outlet.us/ adidas stan smith
http://www.katespade-bags.us/ kate spade bags
http://www.skechers.in.net/ skechers sandals
http://www.kd11-shoes.us/ kd 11
http://www.newjordans.in.net/ jordan retro 11
http://www.pandora--jewelry.co.uk/ pandora rings
http://www.fitflop-shoes.ca/ fitflop sandals
http://www.kd11shoes.us/ kd shoes
http://www.doudoune-moncler.fr/ moncler doudoune
http://www.adidaszxflux.us/ yeezy boost 350 v2
http://www.goyards.ca/ goyard canada
http://www.adidastrainers-uk.co.uk/ adidas uk
http://www.bijoux-pandora.fr/ pandora
http://www.yeezys.fr/ yeezy boost
http://www.adidaschaussure.fr/ adidas
http://www.air-max.us/ nike
http://www.uggsforwomen.us/ ugg
http://www.nikeairmax.fr/ nike fr
http://www.pandora-jewelrys.ca/ pandora earrings
cora님의 댓글
cora 작성일
http://www.ecco.in.net/ ecco sandals
http://www.clarks.in.net/ clarks shoes
http://www.eccoshoesoutlet.us.org/ ecco mens shoes
http://www.salomon-shoes.us.org/ salomon running shoes
http://www.salomons.us.org/ salomon running shoes
http://www.boseheadphones.us/ bose soundlink mini
http://www.stussy.com.co/ stussy clothing
http://www.stussyclothing.us.com/ stussy hoodie
http://www.levis.us.org/ levis jeans
http://www.bose.us.org/ bose
http://www.katespadebags.us.org/ kate spade outlet
http://www.timberlands.us.org/ timberland shoes
http://www.adidas-eqt.us.com/ adidas eqt support
http://www.levis.us.com/ levi's
http://www.katespadepurses.us.org/ kate spade outlet
http://www.katespade-handbags.us.org/ kate spade outlet
tawnya님의 댓글
tawnya 작성일
http://www.stussy.com.co/ stussy sweatshirt
http://www.katespade-handbags.us.org/ kate spade bags
http://www.boseheadphones.us/ bose speakers
http://www.adidas-eqt.us.com/ adidas eqt
http://www.salomons.us.org/ salomon shoes
http://www.bose.us.org/ bose headphones
http://www.katespadebags.us.org/ kate spade purses
http://www.eccoshoesoutlet.us.org/ ecco sandals
http://www.ecco.in.net/ ecco shoes women
http://www.katespadepurses.us.org/ kate spade
http://www.timberlands.us.org/ timberland outlet
http://www.levis.us.com/ levis outlet
http://www.stussyclothing.us.com/ stussy sweatshirt
http://www.clarks.in.net/ clarks outlet
http://www.salomon-shoes.us.org/ salomon shoes
http://www.levis.us.org/ levis jeans
wangshi57님의 댓글
wangshi57 작성일
http://www.ultra-boost.ca/ adidas originals ultra boost
http://www.redbottomslouboutinshoes.us.com/ louboutin shoes
http://www.katespades.ca/ kate spade handbags
http://www.pandora-jewelrys.ca/ pandora earrings
http://www.yeezy--shoes.co.uk/ yeezy boos
http://www.monclers.us.com/ moncler jacket
http://www.birkenstock-sandals.ca/ birkenstock shoes
http://www.lebron16-shoes.us/ lebron james shoes
http://www.pandorajewelrycharms.ca/ pandora
http://www.red-bottoms.us.org/ louboutin
http://www.skechers.in.net/ skechers sneakers
http://www.yeezys.fr/ adidas yeezy
http://www.zxflux.us/ yeezy shoes
http://www.skechers-shoes.ca/ skechers
http://www.uggboots-outlet.us/ ugg boots
http://www.newjordans.in.net/ jordan retro 11
http://www.nikeuktrainers.co.uk/ nike uk
http://www.yeezyshoes.ca/ yeezy boost 350
http://www.monclerjacket.us/ moncler
http://www.adidas--trainers.org.uk/ adidas trainers
http://www.bracelet-pandora.fr/ pandora
http://www.christianlouboutins.fr/ louboutin
http://www.bijoux-pandora.fr/ bijoux pandora
http://www.katespades.co.uk/ kate spade outlet
http://www.monclers.fr/ doudoune moncler
http://www.giuseppezanottis.us/ isabel marant
http://www.salomonshoes.ca/ salomon speedcross 4
http://www.doudoune-moncler.fr/ moncler homme
http://www.redbottom-shoes.co.uk/ louboutin shoes
http://www.nike--trainers.org.uk/ nike shoes
http://www.nikeairmax90.ca/ nike air max
http://www.airmax90.fr/ nike air max 97
http://www.kate-spadepurses.us/ kate spade handbags
http://www.goyards.ca/ goyard tote
http://www.adidasshoes-outlet.us/ adidas superstar
http://www.goldengoosesneakerssale.us/ golden goose sneakers sale
http://www.adidas-nmd.fr/ Adidas Nmd Femme
http://www.fjallravenkanken-backpack.us/ fjallraven
http://www.nikeairmax270.ca/ air max
http://www.airjordan11.fr/ jordan 11
http://www.jordan--shoes.us.com/ jordan shoes
http://www.pandora-bracelet.fr/ pandora bracelet
http://www.christianlouboutins.ca/ christian louboutin
http://www.pandoraukcharms.org.uk/ pandora uk
http://www.jordan-retro11.us.com/ jordan 11
http://www.pandora--jewelry.us.org/ pandora rings
http://www.fila-shoes.us/ fila shoes
http://www.adidaszxflux.us/ adidas zx flux
http://www.skechers-shoe.us.com/ skechers
http://www.philipppleinoutlet.us/ philipp plein shoes
http://www.jordan11.us.com/ jordan retro 11
http://www.lebron-16shoes.us/ lebron james shoes
http://www.yeezy.in.net/ yeezy boost 350 v2
http://www.uggslippers.ca/ ugg
http://www.bottesugg.fr/ bottes ugg
http://www.moncler-uk.co.uk/ moncler jacket mens
http://www.ugg-pascher.fr/ ugg pas cher
http://www.goyard.org.uk/ goyard bag
http://www.adidaschaussure.fr/ adidas stan smith
http://www.air-max.us/ nike air max plus
http://www.vans--shoes.us.com/ vans slip on
http://www.nikeoffwhite.us.com/ off white
http://www.pandoraukrings.co.uk/ pandora earrings
http://www.adidaseqtsupportadv.us/ adidas eqt
http://www.nmds.ca/ adidas nmd
http://www.chaussuresskechers.fr/ skechers femme
http://www.goyardhandbags.us/ goyard tote
http://www.balenciaga.us.org/ balenciaga sneakers
http://www.nikeoffwhiteshoes.us/ off white clothing
http://www.uggboots-uk.co.uk/ ugg uk
http://www.red-bottoms.org.uk/ christian louboutin
http://www.red-bottoms.ca/ christian louboutin
http://www.nikeairmax-2019.us.com/ nike air max 270
http://www.adidaseqt.us.org/ adidas eqt
http://www.nike-vapormax.ca/ nike air vapormax flyknit
http://www.longchampbags.ca/ longchamp canada
http://www.nikeairmax.fr/ nike
http://www.airmax-2019.us.com/ air max 2019
http://www.nike-canada.ca/ nike outlet
http://www.yeezy-750.us/ yeezy boost 750
http://www.salomon.us.org/ salomon xa pro 3d
http://www.long-champs.us.com/ longchamp tote
http://www.jordan11shoes.us.com/ new jordans
http://www.nike-airmax.ca/ nike ca
http://www.uggsforwomen.us/ ugg boots
http://www.filas.us.org/ fila sneakers
http://www.golden-goosesneakers.us.com/ golden goose
http://www.jordan-11.fr/ jordan 11
http://www.adidasyeezyboost.fr/ adidas yeezy
http://www.salomon-chaussures.fr/ salomon speedcross
http://www.kd11shoes.us/ kevin durant
http://www.balenciagas.ca/ balenciaga
http://www.fitflop-shoes.ca/ fitflop canada
http://www.adidascanada-shoes.ca/ adidas
http://www.nmd.us.org/ nmd
http://www.goldengoosesale.us/ golden goose
http://www.monclers.ca/ moncler sale
http://www.fjallravenkankens.us/ fjallraven kanken
http://www.mizunos.us/ mizuno running shoes
http://www.bijouxpandoras.fr/ pandora
http://www.curry-5shoes.us/ curry 4
http://www.adidastrainers-uk.co.uk/ adidas shoes
http://www.louboutin-shoesuk.co.uk/ christian louboutin
http://www.nikebasketballshoes.us/ basketball shoes
http://www.redbottoms-shoes.us.org/ christian louboutin
http://www.chaussuresalomon.fr/ salomon speedcross 4
http://www.chaussure-adidas.fr/ adidas ultra boost
http://www.yeezy-950.us/ yeezy 750
http://www.pandoracanadacharms.ca/ pandora rings
http://www.chaussurelouboutinpascher.fr/ christian louboutin
http://www.adidas--yeezy.co.uk/ yeezy boost
http://www.pandora--jewelry.co.uk/ pandora uk
http://www.adidasboostoutlet.us/ adidas outlet
http://www.katespade-bags.us/ kate spade handbags
http://www.jordanretro11.in.net/ jordan shoes
http://www.adidasyeezyshoes.co.uk/ yeezy boost
http://www.nike-basketballshoes.us.com/ kyrie 5
http://www.pandoras.in.net/ pandora
http://www.chaussure-yeezy.fr/ yeezy boost 350 v2
http://www.ultraboost-uncaged.us/ adidas ultra boost
http://www.philipppleins.us/ philipp plein outlet
http://www.yeezy-500.us/ yeezy
http://www.birkenstock.com.co/ birkenstock sale
http://www.salomonboots.co.uk/ salomon boots
http://www.adidasnmds.us/ adidas nmd
http://www.jordan11.ca/ jordan 11
http://www.jordan-11.co.uk/ jordan shoes
http://www.mizuno-shoes.us/ mizuno wave rider
http://www.goyard.in.net/ goyard tote
http://www.yeezyboost-350v2.fr/ adidas yeezy
http://www.balenciagas.co.uk/ balenciaga shoes
http://www.giuseppezanottisneakers.us/ giuseppe zanotti sneakers
http://www.pandorajewelrycharms.org.uk/ pandora rings
http://www.kd11-shoes.us/ nike kd
yuanlin62님의 댓글
yuanlin62 작성일
http://www.golden-goosesneakers.us.com/ golden goose shoes
http://www.jordan11.ca/ jordan retro 11
http://www.yeezyboost-350v2.fr/ yeezy boost
http://www.skechers.in.net/ skechers
http://www.katespades.co.uk/ kate spade
http://www.adidastrainers-uk.co.uk/ adidas shoes
http://www.katespade-bags.us/ kate spade purses
http://www.kd11-shoes.us/ nike kd
http://www.goyard.org.uk/ goyard wallet,goyard london
http://www.air-max.us/ nike
http://www.airmax-2019.us.com/ nike air max 2019
http://www.redbottom-shoes.co.uk/ louboutin
http://www.birkenstock.com.co/ birkenstock
http://www.jordan11.us.com/ jordan 11
http://www.jordan-11.co.uk/ jordan 11
http://www.lebron16-shoes.us/ lebron
http://www.uggsforwomen.us/ ugg
http://www.goldengoosesale.us/ golden goose shoes
http://www.pandoracanadacharms.ca/ pandora rings
http://www.nikeoffwhite.us.com/ off white
http://www.chaussuresalomon.fr/ chaussure salomon
http://www.adidasyeezyboost.fr/ yeezy
http://www.ultra-boost.ca/ adidas ultra boost
http://www.goyard.in.net/ goyard bag
http://www.nikebasketballshoes.us/ james harden shoes
http://www.mizunos.us/ mizuno
http://www.newjordans.in.net/ jordan 11
http://www.yeezys.fr/ yeezy boost
http://www.ultraboost-uncaged.us/ adidas ultra boost
http://www.red-bottoms.org.uk/ christian louboutin
http://www.adidas--yeezy.co.uk/ adidas yeezy
http://www.kd11shoes.us/ kd 10
http://www.pandora-bracelet.fr/ pandora
http://www.bijouxpandoras.fr/ bague pandora
http://www.mizuno-shoes.us/ mizuno
http://www.birkenstock-sandals.ca/ birkenstock
http://www.goyards.ca/ goyard wallet
http://www.airmax90.fr/ air max 90
http://www.louboutin-shoesuk.co.uk/ christian louboutin
http://www.adidasyeezyshoes.co.uk/ yeezy
http://www.balenciagas.ca/ balenciaga
http://www.yeezy-500.us/ yeezy boost 350
http://www.adidasnmds.us/ adidas shoes
http://www.adidaseqt.us.org/ adidas shoes
http://www.fjallravenkankens.us/ fjallraven kanken
http://www.yeezy-950.us/ yeezy 350
http://www.red-bottoms.ca/ red bottoms
http://www.giuseppezanottis.us/ giuseppe zanotti sneakers
http://www.fitflop-shoes.ca/ fitflop shoes
http://www.salomon.us.org/ salomon xa pro 3d
http://www.balenciagas.co.uk/ balenciaga runners
http://www.lebron-16shoes.us/ nike lebron
http://www.nikeairmax.fr/ nike
http://www.doudoune-moncler.fr/ moncler
http://www.uggslippers.ca/ ugg canada
http://www.fjallravenkanken-backpack.us/ fjallraven kanken
http://www.nmd.us.org/ adidas shoes
http://www.salomonboots.co.uk/ salomon
http://www.pandora--jewelry.us.org/ pandora jewelry
http://www.monclerjacket.us/ moncler sale
http://www.nikeoffwhiteshoes.us/ off white clothing
http://www.bracelet-pandora.fr/ pandora
http://www.yeezy--shoes.co.uk/ yeezy boos
http://www.fila-shoes.us/ fila shoes womens
http://www.red-bottoms.us.org/ christian louboutin
http://www.monclers.us.com/ moncler sale
http://www.monclers.ca/ moncler sale
http://www.nike--trainers.org.uk/ nike trainers
http://www.adidasboostoutlet.us/ adidas shoes for men
http://www.nikeairmax-2019.us.com/ nike air max
http://www.filas.us.org/ fila sneakers
http://www.adidaschaussure.fr/ adidas
http://www.vans--shoes.us.com/ white vans
http://www.philipppleinoutlet.us/ philipp plein shoes
http://www.chaussuresskechers.fr/ skechers homme
http://www.pandora-jewelrys.ca/ pandora jewelry
http://www.uggboots-outlet.us/ ugg
http://www.yeezyshoes.ca/ yeezy boost 350 v2
http://www.chaussure-yeezy.fr/ yeezy
http://www.skechers-shoe.us.com/ skechers outlet
http://www.nike-airmax.ca/ nike ca
http://www.redbottomslouboutinshoes.us.com/ red bottom shoes
http://www.balenciaga.us.org/ balenciaga
http://www.uggboots-uk.co.uk/ ugg uk
http://www.goldengoosesneakerssale.us/ golden goose outlet
http://www.nikeairmax90.ca/ nike air max 90
http://www.pandorajewelrycharms.ca/ pandora jewelry
http://www.adidas--trainers.org.uk/ adidas
http://www.airjordan11.fr/ jordan 11
http://www.pandoras.in.net/ pandora jewelry
http://www.longchampbags.ca/ longchamp handbags
http://www.nike-vapormax.ca/ vapormax
http://www.adidaszxflux.us/ adidas zx flux
http://www.chaussure-adidas.fr/ adidas ultra boost
http://www.jordan11shoes.us.com/ air jordan
http://www.pandoraukrings.co.uk/ pandora rings
http://www.adidaseqtsupportadv.us/ adidas originals eqt
http://www.philipppleins.us/ philipp plein t shirt
http://www.nikeairmax270.ca/ nike off white
http://www.christianlouboutins.fr/ louboutin
http://www.nike-basketballshoes.us.com/ lebron 16
http://www.pandorajewelrycharms.org.uk/ pandora charms
http://www.giuseppezanottisneakers.us/ giuseppe
http://www.salomon-chaussures.fr/ salomon speedcross 4
http://www.yeezy.in.net/ yeezy boost 350
http://www.christianlouboutins.ca/ christian louboutin shoes
http://www.monclers.fr/ moncler femme
http://www.adidascanada-shoes.ca/ adidas canada
http://www.nike-canada.ca/ nike shoes
http://www.nikeuktrainers.co.uk/ nike uk
http://www.long-champs.us.com/ longchamp bag
http://www.adidasshoes-outlet.us/ adidas trainers
http://www.goyardhandbags.us/ goyard tote
http://www.zxflux.us/ adidas zx flux
http://www.bijoux-pandora.fr/ bague pandora
http://www.jordanretro11.in.net/ jordan shoes
http://www.jordan-11.fr/ jordan,jordan 13
http://www.bottesugg.fr/ ugg pas cher
http://www.ugg-pascher.fr/ ugg outlet
http://www.chaussurelouboutinpascher.fr/ christian louboutin
http://www.salomonshoes.ca/ salomon speedcross 4
http://www.jordan--shoes.us.com/ jordan shoes
http://www.kate-spadepurses.us/ kate spade outlet
http://www.katespades.ca/ kate spade bags
http://www.skechers-shoes.ca/ skechers go walk
http://www.jordan-retro11.us.com/ jordan retro
http://www.curry-5shoes.us/ curry 5
http://www.pandoraukcharms.org.uk/ pandora charms
http://www.redbottoms-shoes.us.org/ christian louboutin
http://www.yeezy-750.us/ yeezy boost 750
http://www.nmds.ca/ adidas originals nmd
http://www.adidas-nmd.fr/ Nmd
http://www.moncler-uk.co.uk/ moncler jacket
http://www.pandora--jewelry.co.uk/ pandora rings
lunhui64님의 댓글
lunhui64 작성일
http://www.filas.us.org/ fila sneakers
http://www.longchampbags.ca/ longchamp
http://www.philipppleinoutlet.us/ philipp plein shoes
http://www.balenciaga.us.org/ balenciaga bag
http://www.yeezyshoes.ca/ yeezy boost 350
http://www.curry-5shoes.us/ curry 5
http://www.monclers.ca/ moncler
http://www.chaussuresskechers.fr/ skechers femme
http://www.pandora-bracelet.fr/ bijoux pandora
http://www.ultraboost-uncaged.us/ adidas boost
http://www.chaussure-adidas.fr/ adidas ultra boost
http://www.red-bottoms.us.org/ red bottoms
http://www.christianlouboutins.ca/ red bottom shoes
http://www.jordan-11.co.uk/ jordan 12
http://www.redbottoms-shoes.us.org/ christian louboutin
http://www.adidaszxflux.us/ adidas ultra boost
http://www.balenciagas.ca/ balenciaga bag
http://www.monclers.fr/ moncler femme
http://www.chaussurelouboutinpascher.fr/ louboutin femme
http://www.golden-goosesneakers.us.com/ golden goose shoes
http://www.mizuno-shoes.us/ mizuno wave rider
http://www.pandoraukrings.co.uk/ pandora charms
http://www.lebron-16shoes.us/ nike lebron
http://www.skechers-shoe.us.com/ skechers sandals
http://www.adidas--trainers.org.uk/ adidas trainers
http://www.lebron16-shoes.us/ lebron 16
http://www.kate-spadepurses.us/ kate spade purses
http://www.adidaseqtsupportadv.us/ adidas eqt
http://www.red-bottoms.org.uk/ louboutin heels
http://www.nike-airmax.ca/ air max 97
http://www.nike--trainers.org.uk/ nike air max
http://www.jordanretro11.in.net/ jordan 11
http://www.uggsforwomen.us/ ugg boots
http://www.skechers.in.net/ skechers sneakers
http://www.nikeairmax90.ca/ air max 90
http://www.goyards.ca/ goyard tote
http://www.doudoune-moncler.fr/ moncler homme
http://www.zxflux.us/ zx flux
http://www.pandorajewelrycharms.org.uk/ pandora
http://www.vans--shoes.us.com/ vans shoes
http://www.fjallravenkankens.us/ fjallraven kanken
http://www.chaussure-yeezy.fr/ yeezy boost
http://www.fila-shoes.us/ fila mens shoes
http://www.bijoux-pandora.fr/ bague pandora
http://www.goyard.in.net/ goyard wallet
http://www.airjordan11.fr/ air jordan
http://www.airmax90.fr/ nike air max 95
http://www.bijouxpandoras.fr/ bracelet pandora
http://www.mizunos.us/ mizuno running shoes
http://www.uggboots-uk.co.uk/ ugg uk
http://www.nmd.us.org/ adidas originals nmd
http://www.air-max.us/ air max
http://www.nikebasketballshoes.us/ nike basketball shoes
http://www.nike-basketballshoes.us.com/ nike basketball shoes
http://www.adidaschaussure.fr/ chaussure adidas
http://www.uggboots-outlet.us/ uggs for women
http://www.goyard.org.uk/ goyard uk
http://www.giuseppezanottis.us/ isabel marant
http://www.pandora--jewelry.us.org/ pandora bracelet
http://www.bottesugg.fr/ ugg
http://www.redbottom-shoes.co.uk/ louboutin heels
http://www.jordan--shoes.us.com/ jordan 11
http://www.fjallravenkanken-backpack.us/ fjallraven kanken
http://www.redbottomslouboutinshoes.us.com/ red bottom shoes
http://www.nikeoffwhiteshoes.us/ off white
http://www.nmds.ca/ adidas nmd
http://www.chaussuresalomon.fr/ salomon
http://www.balenciagas.co.uk/ balenciaga shoes
http://www.nike-vapormax.ca/ nike air vapormax
http://www.birkenstock.com.co/ birkenstock shoes
http://www.newjordans.in.net/ new jordans
http://www.pandoracanadacharms.ca/ pandora bracelet
http://www.adidasshoes-outlet.us/ adidas superstar
http://www.christianlouboutins.ca/ louboutin
http://www.moncler-uk.co.uk/ moncler jacket mens
http://www.long-champs.us.com/ longchamp
http://www.katespades.co.uk/ kate spade outlet
http://www.red-bottoms.ca/ red bottoms
http://www.redbottom-shoes.co.uk/ red bottom shoes
http://www.salomon-chaussures.fr/ salomon speedcross
http://www.airmax-2019.us.com/ nike air max 90
http://www.yeezy-750.us/ yeezy boost 350
http://www.filas.us.org/ fila shoes
http://www.mizuno-shoes.us/ mizuno
http://www.skechers.in.net/ skechers boots
http://www.giuseppezanottis.us/ giuseppe zanotti
http://www.adidasboostoutlet.us/ adidas
http://www.adidasnmds.us/ adidas shoes
http://www.giuseppezanottisneakers.us/ isabel marant sneakers
http://www.doudoune-moncler.fr/ moncler femme
http://www.nike-basketballshoes.us.com/ curry 5
http://www.chaussure-adidas.fr/ adidas ultra boost
http://www.ultraboost-uncaged.us/ adidas ultra boost
http://www.air-max.us/ nike air max 90
http://www.nikeairmax270.ca/ nike air max 270
http://www.goyards.ca/ goyard tote
http://www.adidas-nmd.fr/ Chaussure Adidas
http://www.jordan--shoes.us.com/ new jordans
http://www.chaussuresskechers.fr/ skechers homme
http://www.ultra-boost.ca/ adidas originals ultra boost
http://www.newjordans.in.net/ jordan retro 11
http://www.adidas--yeezy.co.uk/ adidas yeezy
http://www.pandoraukrings.co.uk/ pandora uk
http://www.zxflux.us/ adidas zx flux
http://www.bracelet-pandora.fr/ bague pandora
http://www.adidastrainers-uk.co.uk/ adidas trainers
http://www.ugg-pascher.fr/ ugg
http://www.monclers.us.com/ moncler jacket mens
http://www.nikeairmax-2019.us.com/ nike air max 2019
http://www.chaussuresalomon.fr/ salomon speedcross
http://www.yeezyboost-350v2.fr/ yeezy boost 350
http://www.uggslippers.ca/ ugg slippers
http://www.fjallravenkanken-backpack.us/ fjallraven kanken backpack
http://www.pandoras.in.net/ pandora bracelet
http://www.lebron16-shoes.us/ nike lebron
http://www.adidasyeezyshoes.co.uk/ yeezy boost
http://www.goyard.org.uk/ goyard tote
http://www.philipppleinoutlet.us/ philipp plein outlet
http://www.adidaseqtsupportadv.us/ adidas originals eqt
http://www.salomonboots.co.uk/ salomon
http://www.louboutin-shoesuk.co.uk/ christian louboutin uk
http://www.chaussure-yeezy.fr/ yeezy
http://www.jordan-11.co.uk/ jordan 11
http://www.jordan11.us.com/ new jordans
http://www.yeezys.fr/ yeezy boost
http://www.goyardhandbags.us/ goyard tote
http://www.monclers.ca/ moncler sale
http://www.lebron-16shoes.us/ lebron 15
http://www.yeezy.in.net/ adidas yeezy
http://www.chaussurelouboutinpascher.fr/ christian louboutin
http://www.pandora-bracelet.fr/ bracelet pandora
http://www.nikeairmax.fr/ air max
http://www.philipppleins.us/ philipp plein
http://www.uggboots-outlet.us/ ugg boots
http://www.nmds.ca/ adidas shoes
http://www.curry-5shoes.us/ curry 4
http://www.redbottoms-shoes.us.org/ red bottom shoes
brooklyn님의 댓글
brooklyn 작성일
http://www.boseheadphones.us/ bose
http://www.timberlands.us.org/ timberland shoes
http://www.levis.us.org/ levis jeans
http://www.levis.us.com/ levis jeans
http://www.stussyclothing.us.com/ stussy
http://www.ecco.in.net/ ecco shoes
http://www.clarks.in.net/ clarks boots
http://www.eccoshoesoutlet.us.org/ ecco outlet
http://www.stussy.com.co/ stussy hoodie
http://www.adidas-eqt.us.com/ adidas eqt support
http://www.katespade-handbags.us.org/ kate spade outlet
http://www.salomon-shoes.us.org/ salomon speedcross
http://www.katespadebags.us.org/ kate spade purses
http://www.salomons.us.org/ salomon speedcross
http://www.bose.us.org/ bose
http://www.katespadepurses.us.org/ kate spade handbags
lehuan43님의 댓글
lehuan43 작성일
http://www.burberry-bags.us.com/ burberry handbags
http://www.ray--bansunglassess.us.com/ ray ban eyeglasses
http://www.northfacejacketoutlets.us.com/ north face
http://www.nikekdshoes.us.com/ kd 9
http://www.pandora--jewelrys.us.com/ pandora earrings
http://www.redbottom--shoes.us.com/ louboutin
http://www.monclerjacketwomens.us.com/ moncler jacket womens
http://www.redbottoms-louboutin.us.com/ louboutin shoes
http://www.rayban--glasses.us.com/ ray ban glasses
http://www.louboutinredbottoms.us.com/ louboutin shoes
http://www.nikeairmax97.co.uk/ nike shoes
http://www.monclers.uk/ moncler coat
http://www.airmax90shoes.us.com/ nike vapormax
http://www.nike--shoes.co.uk/ nike air max
http://www.cartier-bracelet.us.com/ cartier glasses
http://www.nikeair-max90.co.uk/ nike vapormax
http://www.nike-airmax-2018.us.com/ nike air max 2018
http://www.salvatore-ferragamo.us.com/ ferragamo
http://www.jordan11spacejams.us.com/ jordan retro 12
http://www.ralphlauren--polo.us.com/ ralph lauren outlet
http://www.adidasyeezy-350.us.com/ yeezy boost
http://www.fitflop--sandals.us.com/ fitflop
http://www.adidas-ultraboost.us.com/ adidas ultra boost
http://www.adidas-yeezy-shoes.us.com/ Yeezy Shoes
http://www.adidasnmd-womens.us.com/ adidas nmd womens
http://www.katespadepurses.us.com/ kate spade bags
http://www.airmax-2018.us.com/ air max 90
http://www.salomon-boots.us.com/ salomon speedcross 3
http://www.balenciaga--shoes.us.com/ balenciaga shoes men
http://www.pandora-jewelrybracelet.us.com/ pandora,pandora charms
http://www.mcm--bags.us.com/ mcm
http://www.nikeairmax-95.us.com/ nike air max 95 mens
http://www.ed-hardys.us.com/ ed hardy jeans
http://www.asicss.us.com/ asics
http://www.pandorajewelryscharms.us.com/ pandora jewelry
http://www.truereligion--jeans.us.com/ true religion hoodie
http://www.stephen-curry-shoes.us.com/ curry 4 shoes
http://www.kd10-shoes.us.com/ nike kd
http://www.ferragamoshoess.us.com/ ferragamo
http://www.burberrys.org.uk/ burberry purses
http://www.salomonshoes.co.uk/ salomon boots
http://www.ultra--boost.us.com/ adidas originals ultra boost
http://www.air-max-270.us.com/ nike air max 270
http://www.nikeairmax-97.us.com/ air max 97
http://www.jordans11shoes.us.com/ jordan 11 retro
http://www.longchampbackpack.us.com/ longchamp handbag
http://www.kyrie-irving-shoes.us.com/ kyrie
http://www.mcms.us.com/ mcm bags
http://www.longchampbag.us.com/ longchamp
http://www.bvlgaris.us.com/ bvlgari wallet
http://www.true--religion.us.com/ true religion jeans for women
http://www.huaraches.us.com/ nike air huarache
http://www.yeezyboost350shoes.us.com/ adidas yeezy
http://www.nikeairmax270.org.uk/ nike air max 97
http://www.supreme--clothing.us.com/ supreme clothing
http://www.jimmychooheels.us.com/ jimmy choo heels
http://www.air-max-90.us.com/ air max
http://www.pandoraearrings.us.com/ pandora rings
http://www.yeezyboost350--v2.us.com/ yeezy boost 350 v2
http://www.asics--shoes.us.com/ asics shoes
http://www.jordan--11.us.com/ jordan
http://www.nikeairvapormaxflyknit.us.com/ nike air max 90
http://www.goyardbag.us.com/ goyard wallet
http://www.curry4-shoes.us.com/ curry 4 shoes
http://www.adidasoriginalsultraboost.us.com/ adidas ultra boost uncaged
http://www.james-hardenshoes.us.com/ harden vol 2
http://www.salomon--shoes.us.com/ Salomon Boots
http://www.fitflop--shoes.us.com/ fitflop sale
http://www.coachbags-outlet.us.com/ coach purses
http://www.moncler-coat.us.com/ moncler jacket
http://www.pandora-charmsjewelry.us.com/ pandora
http://www.monclerjacketmens.us.com/ moncler coat
http://www.moncler--jacket.us.com/ moncler jacket womens
http://www.chrome--hearts.us.com/ chrome hearts sunglasses
http://www.mulberry-handbags.us.com/ mulberry bayswater
http://www.adidasnmdrunnerr1.us.com/ didas ultra boost
http://www.jordanretro11-shoes.us.com/ jordan 11
http://www.michaelkors-handbagss.us.com/ mk handbags
http://www.barbourjackets.co.uk/ barbour
http://www.jordan11.co.uk/ air jordan
http://www.airjordan11spacejam.us.com/ jordan retro 11
http://www.katespadebags.us.com/ kate spade
http://www.pumarihannafenty.us.com/ puma shoes
http://www.salomonspeedcross3.us.com/ salomon xa pro 3d
http://www.adidas-yeezyboost350.us.com/ adidas yeezy
http://www.ralphlaurenspoloshirts.us.com/ ralph lauren outlet
http://www.birkenstock--sandals.us.com/ birkenstock outlet
http://www.polo-ralph-lauren.org.uk/ ralph lauren outlet
http://www.christianlouboutinredbottoms.us.com/ louboutin
http://www.air-max-95.us.com/ air max 95 black
http://www.balenciagas-sneakers.us.com/ balenciaga trainers
http://www.hermes--belt.us.com/ hermes
http://www.kyrie-4.us.com/ kyire 4
http://www.northface-jacket.us.com/ north face coats
http://www.nike-airmax270.us.com/ nike air max 90
http://www.pandorauk.us.com/ pandora charms
http://www.pandora-jewelrysale.us.com/ pandora jewelry
http://www.oakley--glasses.us.com/ oakley eyeglasses
http://www.monclerjacket.org.uk/ moncler jacket mens
http://www.mbts.us.com/ mbt
http://www.vapormaxs.us.com/ nike vapormax
http://www.kevin-durant-shoes.us.com/ kd 11
http://www.adidasoriginalsnmd.us.com/ adidas nmd
http://www.burberry--scarf.us.com/ burberry shirt
http://www.pandoras-jewelrys.us.com/ pandora charms
http://www.michael-kors-bags.us.com/ mk handbags
http://www.katespade--outlet.us.com/ kate spade handbags
http://www.prada--bags.us.com/ prada wallet
http://www.fitflops-sale.us.com/ fitflops clearance
http://www.air-max-97.us.com/ air max 97
http://www.airmax95.co.uk/ nike air max 95 mens
http://www.nike-huaraches.us.com/ huarache shoes
http://www.goyardbackpack.us.com/ goyard bag
http://www.lacosteshirts.us.com/ lacoste polo shirts
http://www.pandorajewelryrings.us.com/ pandora bracelet
http://www.airmax270.co.uk/ nike air max
http://www.valentino--shoes.us.com/ valentino heels
http://www.eccoshoesoutlets.us.com/ ecco sandals
http://www.montblancs.us.com/ mont blanc outlet
http://www.adidas-superstarshoes.us.com/ adidas superstar mens
http://www.lebron15-shoes.us.com/ basketball shoes
http://www.birkenstocksandalssale.us.com/ birkenstock
http://www.pandora--rings.us.com/ Pandora Charms
http://www.nikeairmax-90.us.com/ nike air max 90
http://www.chromeheartsjewelrys.us.com/ chrome hearts necklace
http://www.fitflopsshoes.us.com/ fitflop
http://www.prada--handbags.us.com/ prada purse
http://www.supremeshirt.us.com/ supreme clothing
http://www.celines.us.com/ celine handbags
http://www.hermesbirkin-handbags.us.com/ Hermes Handbags
http://www.nikelebron15.us.com/ nike lebron
http://www.polo-ralphlauren-outlet.us.com/ polo ralph lauren
http://www.chromehearts-jewelry.us.com/ chrome hearts pendant
http://www.nike--vapormax.us.com/ vapormax
http://www.coach--bags.us.com/ coach outlet
http://www.under-armour-shoes.us.com/ under armour shoes
http://www.skechers--shoes.us.com/ skechers
xiuying23님의 댓글
xiuying23 작성일
![]() 비밀글 입니다.
비밀글 입니다.
evelyn님의 댓글
evelyn 작성일
http://www.adidassuperstars.us/ adidas superstar
http://www.stussy.com.co/ stussy
http://www.nikeairmaxshoes.us.org/ nike store
http://www.adidasshoesoutlet.us.org/ adidas trainers
http://www.ultraboosts.us.org/ adidas ultra boost
http://www.airmax-97.us.org/ air max 97
http://www.geox.us.com/ geox mens shoes
http://www.chaussurefila.fr/ fila chaussure
http://www.timberlands.us.org/ timberland
http://www.katespade-handbags.us.org/ kate spade outlet
http://www.new-balance.us.com/ new balance 574
http://www.adidas-chaussure.fr/ adidas yeezy
http://www.lebron16.us.org/ lebron 16
http://www.chaussures-salomon.fr/ chaussure salomon
http://www.katespadepurses.us.org/ kate spade
http://www.nmd.in.net/ nmd shoes
http://www.geox.us.org/ geox mens shoes
http://www.salomon-shoes.us.org/ salomon running shoes
http://www.converses.us.org/ converse
http://www.nikebasketballshoes.us.org/ nike basketball
http://www.chaussurebalenciaga.fr/ balenciaga femme
http://www.bose.us.org/ bose
http://www.yeezy-boost350.us.org/ yeezy boost 350
http://www.levis.us.com/ levis outlet
http://www.northfacejacketoutlet.us.com/ north face coats
http://www.airmax-95.us.org/ air max
http://www.ninewestshoes.us.com/ nine west
http://www.puma.in.net/ puma shoes
http://www.vansoldschool.fr/ vans old school
http://www.ecco.in.net/ ecco sandals
http://www.converseshoesoutlet.us.org/ converse
http://www.boseheadphones.us/ bose
http://www.nike-airmax2019.us.com/ nike air max 2019
http://www.pumashoesoutlet.us.org/ puma sneakers
http://www.katespadebags.us.org/ kate spade bags
http://www.nikeshoes-outlet.us.org/ nike shoes
http://www.nikebasketball.us.com/ nike basketball shoes
http://www.supreme.com.co/ supreme hoodie
http://www.supreme-clothing.us.org/ supreme clothing
http://www.adidas-nmd.us.org/ nmd
http://www.mizuno.in.net/ mizuno
http://www.eccoshoesoutlet.us.org/ ecco outlet
http://www.chaussurejordan.fr/ air jordan
http://www.jordan11shoes.us.org/ new jordans
http://www.skechers-outlet.us.org/ skechers
http://www.jordan-4.us.org/ jordan space jams
http://www.fjallravenkanken.us.org/ fjallraven
http://www.jordanretro11.us.org/ jordan retro
http://www.fjallravens.us.com/ fjallraven backpack
http://www.northfaces.us.org/ north face outlet
http://www.converseblanche.fr/ converse homme
http://www.adidas-eqt.us.com/ adidas originals eqt
http://www.coachbagsoutlet.us.org/ coach outlet
http://www.ninewest.us.org/ nine west boots
http://www.nike-chaussure.fr/ nike
http://www.stussyclothing.us.com/ stussy outlet
http://www.braceletpandoras.fr/ bracelet pandora
http://www.salomons.us.org/ salomon speedcross
http://www.yeezysupply.us.org/ adidas yeezy
http://www.jordan12.us.org/ jordan retro 12
http://www.airmax-90.us.org/ nike air max 90
http://www.skechersboots.us.org/ skechers shoes
http://www.new-balance.fr/ new balance
http://www.mizunoshoes.us.org/ mizuno volleyball shoes
http://www.kd11.us.org/ kd 10
http://www.adidasstansmith.us.org/ stan smith
http://www.newbalance574.us.org/ new balance 574
http://www.adidas-ultraboost.us.org/ adidas originals ultra boost
http://www.clarks.in.net/ clarks
http://www.adidaszxflux.us.org/ adidas zx
http://www.airmax-270.us.org/ nike air max 270
http://www.levis.us.org/ levis jeans
http://www.nikeairmax2019.us.org/ nike air max 2019
minerva님의 댓글
minerva 작성일
http://www.vansoldschool.fr/ vans old skool
http://www.skechersboots.us.org/ skechers boots
http://www.coachbagsoutlet.us.org/ coach handbags
http://www.geox.us.org/ geox sneakers
http://www.stussy.com.co/ stussy outlet
http://www.chaussurejordan.fr/ chaussure jordan
http://www.nike-chaussure.fr/ nike chaussure
http://www.jordanretro11.us.org/ jordan shoes
http://www.levis.us.org/ levi's
http://www.nmd.in.net/ adidas originals nmd
http://www.chaussures-salomon.fr/ chaussure salomon homme
http://www.supreme.com.co/ supreme hoodie
http://www.yeezy-boost350.us.org/ adidas yeezy
http://www.timberlands.us.org/ timberland
http://www.ninewest.us.org/ nine west boots
http://www.airmax-270.us.org/ nike air max
http://www.mizunoshoes.us.org/ mizuno volleyball shoes
http://www.jordan11shoes.us.org/ air jordan xi
http://www.airmax-90.us.org/ nike air max
http://www.new-balance.fr/ new balance 574
http://www.nikeairmax2019.us.org/ air max 2019
http://www.northfaces.us.org/ north face coats
http://www.ultraboosts.us.org/ ultra boost uncaged
http://www.new-balance.us.com/ new balance
http://www.katespadepurses.us.org/ kate spade handbags
http://www.salomons.us.org/ salomon
http://www.katespadebags.us.org/ kate spade bags
http://www.boseheadphones.us/ bose wireless speaker
http://www.adidasstansmith.us.org/ adidas stan smith
http://www.adidas-eqt.us.com/ adidas eqt
http://www.jordan12.us.org/ jordan retro 12
http://www.ecco.in.net/ ecco shoes women
http://www.chaussurebalenciaga.fr/ balenciaga
http://www.northfacejacketoutlet.us.com/ north face vest
http://www.adidasshoesoutlet.us.org/ adidas trainers
http://www.yeezysupply.us.org/ yeezy
http://www.skechers-outlet.us.org/ skechers
http://www.converses.us.org/ converse outlet
http://www.fjallravenkanken.us.org/ fjallraven
http://www.braceletpandoras.fr/ bague pandora
http://www.nikeshoes-outlet.us.org/ nike outlet
http://www.chaussurefila.fr/ chaussure fila
http://www.jordan-4.us.org/ air jordan 4
http://www.stussyclothing.us.com/ stussy hoodie
http://www.clarks.in.net/ clarks shoes
http://www.converseshoesoutlet.us.org/ converse
http://www.salomon-shoes.us.org/ salomon boots
http://www.bose.us.org/ bose speakers
http://www.adidas-nmd.us.org/ nmd shoes
http://www.lebron16.us.org/ lebron james shoes
http://www.levis.us.com/ levis outlet
http://www.newbalance574.us.org/ new balance
http://www.adidas-ultraboost.us.org/ ultra boost
http://www.mizuno.in.net/ mizuno volleyball shoes
http://www.nikebasketball.us.com/ mens basketball shoes
http://www.adidaszxflux.us.org/ adidas zx flux
http://www.pumashoesoutlet.us.org/ puma suede
http://www.puma.in.net/ puma sneakers
http://www.converseblanche.fr/ converse
http://www.airmax-97.us.org/ air max
http://www.nikebasketballshoes.us.org/ nike basketball shoes
http://www.fjallravens.us.com/ fjallraven
http://www.nikeairmaxshoes.us.org/ nike air max
http://www.nike-airmax2019.us.com/ nike air max 2019
http://www.adidas-chaussure.fr/ adidas chaussure
http://www.katespade-handbags.us.org/ kate spade handbags
http://www.eccoshoesoutlet.us.org/ ecco shoes
http://www.kd11.us.org/ kd shoes
http://www.adidassuperstars.us/ adidas shoes women
http://www.supreme-clothing.us.org/ supreme shirt
http://www.geox.us.com/ geox shoes
http://www.airmax-95.us.org/ nike air max 95
http://www.ninewestshoes.us.com/ nine west boots
eddie님의 댓글
eddie 작성일
http://www.converseblanche.fr/ converse femme
http://www.jordan-4.us.org/ jordan shoes
http://www.kd11.us.org/ nike kd
http://www.jordan11shoes.us.org/ air jordan
http://www.nikebasketball.us.com/ nike basketball shoes
http://www.adidassuperstars.us/ adidas superstar
http://www.yeezysupply.us.org/ yeezy supply
http://www.northfaces.us.org/ north face vest
http://www.fjallravens.us.com/ fjallraven
http://www.lebron16.us.org/ lebron 16
http://www.newbalance574.us.org/ new balance sneakers
http://www.nike-airmax2019.us.com/ air max 2019
http://www.airmax-270.us.org/ nike air max 270
http://www.adidas-ultraboost.us.org/ ultra boost uncaged
http://www.chaussurejordan.fr/ jordan homme
http://www.ecco.in.net/ ecco shoes
http://www.adidas-chaussure.fr/ adidas chaussure
http://www.nike-chaussure.fr/ nike
http://www.pumashoesoutlet.us.org/ puma suede
http://www.clarks.in.net/ clarks
http://www.adidas-eqt.us.com/ adidas originals eqt
http://www.timberlands.us.org/ timberland shoes
http://www.jordan12.us.org/ air jordan 12
http://www.braceletpandoras.fr/ bijoux pandora
http://www.vansoldschool.fr/ vans old skool
http://www.stussyclothing.us.com/ stussy sweatshirt
http://www.salomon-shoes.us.org/ salomon shoes
http://www.fjallravenkanken.us.org/ fjallraven
http://www.adidasstansmith.us.org/ adidas stan smith
http://www.katespadepurses.us.org/ kate spade outlet
http://www.adidasshoesoutlet.us.org/ adidas outlet
http://www.new-balance.fr/ new balance 574
http://www.bose.us.org/ bose
http://www.stussy.com.co/ stussy outlet
http://www.supreme.com.co/ supreme hoodie
http://www.nikeshoes-outlet.us.org/ nike shoes
http://www.skechers-outlet.us.org/ skechers
http://www.chaussurebalenciaga.fr/ basket balenciaga
http://www.converseshoesoutlet.us.org/ converse
http://www.supreme-clothing.us.org/ supreme clothing
http://www.chaussurefila.fr/ fila femme
http://www.geox.us.org/ geox mens shoes
http://www.coachbagsoutlet.us.org/ coach
http://www.adidaszxflux.us.org/ adidas flux
http://www.geox.us.com/ geox mens shoes
http://www.nmd.in.net/ adidas originals nmd
http://www.ninewest.us.org/ nine west shoes
http://www.mizuno.in.net/ mizuno volleyball shoes
http://www.new-balance.us.com/ new balance outlet
http://www.converses.us.org/ womens converse
http://www.adidas-nmd.us.org/ nmd shoes
http://www.airmax-97.us.org/ air max 97
http://www.ninewestshoes.us.com/ nine west outlet
http://www.katespadebags.us.org/ kate spade handbags
http://www.skechersboots.us.org/ skechers outlet
http://www.jordanretro11.us.org/ jordan 11
http://www.levis.us.org/ levi's
http://www.salomons.us.org/ salomon boots
http://www.airmax-95.us.org/ nike air max
http://www.nikebasketballshoes.us.org/ mens basketball shoes
http://www.eccoshoesoutlet.us.org/ ecco
http://www.puma.in.net/ puma
http://www.ultraboosts.us.org/ adidas originals ultra boost
http://www.katespade-handbags.us.org/ kate spade purses
http://www.chaussures-salomon.fr/ chaussure salomon
http://www.nikeairmaxshoes.us.org/ nike shoes
http://www.airmax-90.us.org/ nike air max women
http://www.boseheadphones.us/ bose
http://www.levis.us.com/ levis outlet
http://www.northfacejacketoutlet.us.com/ north face jacket
http://www.mizunoshoes.us.org/ mizuno
http://www.nikeairmax2019.us.org/ nike air max
http://www.yeezy-boost350.us.org/ yeezy
tawnya님의 댓글
tawnya 작성일
http://www.jordan12.us.org/ jordan 12
http://www.katespadebags.us.org/ kate spade bags
http://www.skechers-outlet.us.org/ skechers outlet
http://www.geox.us.com/ geox mens shoes
http://www.adidaszxflux.us.org/ zx flux
http://www.katespadepurses.us.org/ kate spade handbags
http://www.airmax-270.us.org/ air max
http://www.adidasshoesoutlet.us.org/ adidas trainers
http://www.adidas-eqt.us.com/ adidas eqt
http://www.new-balance.us.com/ new balance outlet
http://www.ninewestshoes.us.com/ nine west
http://www.chaussurefila.fr/ chaussure fila
http://www.timberlands.us.org/ timberland
http://www.newbalance574.us.org/ new balance 574
http://www.airmax-97.us.org/ nike shoes
http://www.chaussurebalenciaga.fr/ chaussure balenciaga
http://www.adidasstansmith.us.org/ adidas stan smith
http://www.adidas-ultraboost.us.org/ ultra boost uncaged
http://www.kd11.us.org/ kd 11
http://www.ultraboosts.us.org/ adidas originals ultra boost
http://www.stussy.com.co/ stussy outlet
http://www.chaussures-salomon.fr/ chaussure salomon homme
http://www.adidas-nmd.us.org/ adidas originals nmd
http://www.puma.in.net/ puma
http://www.converseblanche.fr/ converse homme
http://www.braceletpandoras.fr/ pandora bracelet
http://www.ninewest.us.org/ nine west boots
http://www.northfacejacketoutlet.us.com/ north face outlet
http://www.lebron16.us.org/ lebron 15
http://www.katespade-handbags.us.org/ kate spade bags
http://www.salomon-shoes.us.org/ salomon running shoes
http://www.nikeairmaxshoes.us.org/ nike air max
http://www.new-balance.fr/ new balance homme
http://www.mizunoshoes.us.org/ mizuno shoes
http://www.yeezy-boost350.us.org/ yeezy
http://www.nmd.in.net/ adidas nmd
http://www.boseheadphones.us/ bose
http://www.fjallravens.us.com/ fjallraven kanken backpack
http://www.vansoldschool.fr/ vans old school
http://www.converses.us.org/ converse
http://www.coachbagsoutlet.us.org/ coach handbags
http://www.nikeairmax2019.us.org/ air max 2019
http://www.jordan-4.us.org/ jordan shoes
http://www.bose.us.org/ bose
http://www.stussyclothing.us.com/ stussy clothing
http://www.supreme-clothing.us.org/ supreme
http://www.geox.us.org/ geox mens shoes
http://www.jordanretro11.us.org/ jordan 11
http://www.chaussurejordan.fr/ air jordan
http://www.converseshoesoutlet.us.org/ womens converse
http://www.jordan11shoes.us.org/ air jordan
http://www.northfaces.us.org/ north face outlet
http://www.clarks.in.net/ clarks sandals
http://www.yeezysupply.us.org/ yeezy shoes
http://www.nike-airmax2019.us.com/ nike air max 2019
http://www.nike-chaussure.fr/ chaussure nike
http://www.salomons.us.org/ salomon running shoes
http://www.airmax-95.us.org/ air max
http://www.supreme.com.co/ supreme hoodie
http://www.mizuno.in.net/ mizuno
http://www.ecco.in.net/ ecco shoes women
http://www.nikebasketball.us.com/ nike basketball shoes
http://www.airmax-90.us.org/ air max
http://www.pumashoesoutlet.us.org/ puma
http://www.adidas-chaussure.fr/ adidas chaussure
http://www.nikeshoes-outlet.us.org/ nike air max
http://www.levis.us.com/ levis
http://www.levis.us.org/ levis jeans
http://www.eccoshoesoutlet.us.org/ ecco shoes
http://www.adidassuperstars.us/ adidas shoes women
http://www.nikebasketballshoes.us.org/ nike basketball
http://www.skechersboots.us.org/ skechers outlet
http://www.fjallravenkanken.us.org/ fjallraven
muxiao19님의 댓글
muxiao19 작성일
![]() 비밀글 입니다.
비밀글 입니다.
kelvin님의 댓글
kelvin 작성일
![]() 비밀글 입니다.
비밀글 입니다.
xiuying23님의 댓글
xiuying23 작성일
![]() 비밀글 입니다.
비밀글 입니다.
lehuan43님의 댓글
lehuan43 작성일
http://www.bracelet-pandora.fr/ bracelet pandora
http://www.fila-shoes.us/ fila shoes
http://www.uggboots-outlet.us/ ugg outlet
http://www.adidascanada-shoes.ca/ adidas
http://www.nikeairmax90.ca/ nike air max
http://www.ugg-pascher.fr/ ugg
http://www.uggslippers.ca/ ugg canada
http://www.moncler-uk.co.uk/ moncler jacket
http://www.curry-5shoes.us/ curry 4
http://www.fjallravenkankens.us/ fjallraven
http://www.nike-basketballshoes.us.com/ kd 11
http://www.nike-canada.ca/ nike canada
http://www.redbottom-shoes.co.uk/ christian louboutin
http://www.jordan-retro11.us.com/ jordan shoes
http://www.balenciagas.ca/ balenciaga
http://www.air-max.us/ nike air max 90
http://www.long-champs.us.com/ longchamp
http://www.adidaseqtsupportadv.us/ adidas eqt support adv
http://www.nmd.us.org/ adidas shoes
http://www.redbottoms-shoes.us.org/ red bottoms
http://www.yeezy-950.us/ yeezy boost 950
http://www.uggsforwomen.us/ ugg
http://www.nikeuktrainers.co.uk/ nike air max
http://www.philipppleinoutlet.us/ philipp plein outlet
http://www.goyardhandbags.us/ goyard bag
http://www.yeezyshoes.ca/ yeezy boost 350 v2
http://www.skechers-shoes.ca/ skechers go walk
http://www.pandora--jewelry.co.uk/ pandora jewelry
http://www.jordan-11.co.uk/ jordan shoes
http://www.airmax90.fr/ nike air max 97
http://www.jordan11.ca/ jordan retro 11
http://www.fitflop-shoes.ca/ fitflop
http://www.mizuno-shoes.us/ mizuno
http://www.monclers.fr/ moncler homme
http://www.nikeairmax.fr/ nike air max
http://www.salomon-chaussures.fr/ salomon speedcross
http://www.louboutin-shoesuk.co.uk/ christian louboutin uk
http://www.nike--trainers.org.uk/ nike shoes
http://www.red-bottoms.org.uk/ louboutin
http://www.nikebasketballshoes.us/ steph curry shoes
http://www.adidas--trainers.org.uk/ adidas
http://www.jordan-11.fr/ jordan 11
http://www.yeezy-500.us/ yeezy
http://www.pandora--jewelry.us.org/ pandora rings
http://www.goyards.ca/ goyard
http://www.doudoune-moncler.fr/ moncler
http://www.kate-spadepurses.us/ kate spade purses
http://www.pandoraukcharms.org.uk/ pandora rings
http://www.nikeairmax-2019.us.com/ nike air max 2019
http://www.jordan11shoes.us.com/ jordan 11
http://www.salomonboots.co.uk/ salomon shoes
http://www.jordan11.us.com/ jordan 11
http://www.nikeoffwhiteshoes.us/ off white
http://www.airjordan11.fr/ air jordan
http://www.nikeoffwhite.us.com/ off white sneakers
http://www.adidaseqt.us.org/ adidas eqt support adv
http://www.ultraboost-uncaged.us/ adidas boost
http://www.lebron-16shoes.us/ lebron james shoes
http://www.lebron16-shoes.us/ lebron 16
http://www.christianlouboutins.fr/ louboutin femme
http://www.philipppleins.us/ philipp plein outlet
http://www.jordan--shoes.us.com/ air jordan
http://www.adidasshoes-outlet.us/ adidas trainers
http://www.pandorajewelrycharms.org.uk/ pandora charms
http://www.yeezy.in.net/ yeezy
http://www.jordanretro11.in.net/ jordan shoes
http://www.fjallravenkanken-backpack.us/ fjallraven
http://www.birkenstock.com.co/ birkenstock outlet
http://www.red-bottoms.us.org/ louboutin
http://www.giuseppezanottisneakers.us/ giuseppe zanotti
http://www.goyard.org.uk/ goyard london
http://www.salomon-chaussures.fr/ salomon speedcross 4
http://www.nikeairmax270.ca/ nike air max
http://www.salomonshoes.ca/ salomon speedcross 4
http://www.zxflux.us/ yeezy shoes
http://www.jordan11.us.com/ jordan retro 11
http://www.skechers.in.net/ skechers sneakers
http://www.christianlouboutins.fr/ louboutin homme
http://www.pandoras.in.net/ pandora jewelry
http://www.adidasyeezyboost.fr/ adidas yeezy
http://www.adidascanada-shoes.ca/ adidas outlet
http://www.monclers.fr/ moncler homme
http://www.redbottoms-shoes.us.org/ red bottom shoes
http://www.philipppleinoutlet.us/ philipp plein t shirt
http://www.airmax-2019.us.com/ air max 270
http://www.salomonboots.co.uk/ salomon speedcross 4
http://www.fila-shoes.us/ fila shoes
http://www.air-max.us/ nike
http://www.jordan--shoes.us.com/ new jordans
http://www.filas.us.org/ fila shoes womens
http://www.nikeairmax.fr/ nike air max 90
http://www.giuseppezanottisneakers.us/ giuseppe zanotti
http://www.birkenstock.com.co/ birkenstock shoes
http://www.nmd.us.org/ nmd
http://www.yeezys.fr/ yeezy boost
http://www.salomon.us.org/ salomon shoes
http://www.nike-airmax.ca/ air max
http://www.nikeoffwhiteshoes.us/ off white shoes
http://www.chaussure-yeezy.fr/ yeezy boost 350 v2
http://www.adidaseqtsupportadv.us/ eqt
http://www.jordan-retro11.us.com/ jordan 7
http://www.balenciagas.ca/ balenciaga
http://www.uggslippers.ca/ ugg slippers
http://www.red-bottoms.ca/ red bottoms
http://www.ugg-pascher.fr/ bottes ugg
http://www.nikebasketballshoes.us/ kyrie irving shoes
http://www.yeezyshoes.ca/ yeezy boost 350
http://www.nikeuktrainers.co.uk/ nike uk
http://www.balenciaga.us.org/ balenciaga sneakers
http://www.birkenstock-sandals.ca/ birkenstock sale
http://www.adidas--yeezy.co.uk/ yeezy
http://www.nikeoffwhite.us.com/ off white
http://www.skechers-shoes.ca/ skechers
http://www.moncler-uk.co.uk/ moncler uk
http://www.redbottomslouboutinshoes.us.com/ red bottom shoes
http://www.nike--trainers.org.uk/ nike shoes
http://www.pandora--jewelry.co.uk/ pandora jewelry
http://www.jordan-11.co.uk/ jordan shoes
http://www.katespades.ca/ kate spade handbags
http://www.pandora--jewelry.us.org/ pandora bracelet
http://www.jordan11shoes.us.com/ jordan 11 space jam
http://www.goldengoosesale.us/ golden goose
http://www.jordanretro11.in.net/ air jordan
http://www.monclers.ca/ moncler
http://www.adidasboostoutlet.us/ adidas shoes
http://www.chaussurelouboutinpascher.fr/ christian louboutin
http://www.philipppleins.us/ philipp plein t shirt
http://www.yeezy-500.us/ yeezy boost 350
http://www.pandoraukrings.co.uk/ pandora
http://www.chaussure-adidas.fr/ chaussure adidas
http://www.katespade-bags.us/ kate spade handbags
http://www.goyardhandbags.us/ goyard handbags
http://www.nikeairmax-2019.us.com/ nike air max 2019
http://www.monclers.us.com/ moncler jacket
http://www.kd11shoes.us/ kd 10
http://www.nike-canada.ca/ nike store
http://www.jordan-11.fr/ jordan retro 11
kelvin님의 댓글
kelvin 작성일
http://www.zapatillas-puma.com/ Puma
http://www.northfaces.us.org/ north face outlet
http://www.camisaversace.com/ Camisa Versace Hombre
http://www.skechersboots.us.org/ skechers outlet
http://www.nikeairmax2019.us.org/ nike air max
http://www.supreme.com.co/ supreme shirt
http://www.geox.us.com/ geox sneakers
http://www.yeezysupply.us.org/ adidas yeezy
http://www.nike-airmax2019.us.com/ nike shoes
http://www.geox.us.org/ geox sneakers
http://www.airmax-270.us.org/ nike air max
http://www.eccoshoesoutlet.us.org/ ecco
http://www.kd11.us.org/ kd shoes
http://www.pumashoesoutlet.us.org/ puma suede
http://www.yeezy-boost350.us.org/ yeezy boost 350 v2
http://www.adidas-nmd.us.org/ nmd shoes
http://www.adidas-ultraboost.us.org/ adidas ultra boost
http://www.airmax-90.us.org/ air max
http://www.adidaszxflux.us.org/ adidas flux
http://www.ninewest.us.org/ nine west outlet
http://www.zapatillasnikehombre.com/ Bambas Nike
http://www.nike-chaussure.fr/ nike
http://www.bose.us.org/ bose
http://www.jordan-4.us.org/ air jordan 4
http://www.trajeshugoboss.com/ Camisas Hugo Boss
http://www.new-balance.fr/ new balance
http://www.airmax-95.us.org/ air max
http://www.jordan11shoes.us.org/ new jordans
http://www.adidas-eqt.us.com/ adidas originals eqt
http://www.airmax-97.us.org/ nike air max
http://www.nikeairmaxshoes.us.org/ nike store
http://www.adidassuperstars.us/ adidas shoes women
http://www.camisas-ralphlauren.com/ Camisas Ralph Lauren
http://www.ropaguess.com/ Ropa Guess
http://www.armaniropa.com/ Armani Ropa
http://www.stussy.com.co/ stussy sweatshirt
http://www.chaussurefila.fr/ fila chaussure
http://www.supreme-clothing.us.org/ supreme hoodie
http://www.chaussurebalenciaga.fr/ balenciaga femme
http://www.zapatillas-vans.com/ Zapatillas Vans Mujer
http://www.zapatillas-offwhite.com/ Adidas Off White
http://www.coachbagsoutlet.us.org/ coach handbags
http://www.braceletpandoras.fr/ pandora
http://www.zapatillas-converse.com/ Zapatos Converse
http://www.converses.us.org/ converse shoes
http://www.converseshoesoutlet.us.org/ womens converse
http://www.stussyclothing.us.com/ stussy hoodie
http://www.adidasshoesoutlet.us.org/ adidas
http://www.chaussurejordan.fr/ air jordan
http://www.nikebasketballshoes.us.org/ nike basketball shoes
http://www.converseblanche.fr/ converse Blanche
http://www.mizunoshoes.us.org/ mizuno volleyball shoes
http://www.puma.in.net/ puma shoes
http://www.calvinkleinhombre.com/ Calvin Klein
http://www.katespade-handbags.us.org/ kate spade handbags
http://www.clarks.in.net/ clarks sandals
http://www.katespadebags.us.org/ kate spade outlet
http://www.zapatossocceradidas.com/ Zapatos Soccer Adidas
http://www.nikeshoes-outlet.us.org/ nike store
http://www.adidasstansmith.us.org/ stan smith shoes
http://www.timberlands.us.org/ timberland
http://www.chaussures-salomon.fr/ salomon
http://www.lebron16.us.org/ lebron 15
http://www.mizuno.in.net/ mizuno
http://www.boseheadphones.us/ bose
http://www.levis.us.org/ levis jeans
http://www.ultraboosts.us.org/ adidas ultra boost
http://www.fjallravens.us.com/ fjallraven kanken backpack
http://www.vansoldschool.fr/ vans old school
http://www.nmd.in.net/ adidas nmd
http://www.jordan12.us.org/ jordan retro 12
http://www.northfacejacketoutlet.us.com/ north face vest
http://www.jordanretro11.us.org/ jordan retro 11
http://www.ecco.in.net/ ecco sandals
http://www.fjallravenkanken.us.org/ fjallraven kanken backpack
http://www.zapatoslouboutin.com/ Zapatos Christian Louboutin
http://www.ninewestshoes.us.com/ nine west outlet
http://www.salomons.us.org/ salomon
http://www.adidas-chaussure.fr/ chaussure adidas
http://www.zapatillas-adidas.com/ Zapatillas Adidas
http://www.nikebasketball.us.com/ basketball shoes
http://www.katespadepurses.us.org/ kate spade bags
http://www.newbalance574.us.org/ new balance outlet
http://www.salomon-shoes.us.org/ salomon
http://www.levis.us.com/ levis
http://www.skechers-outlet.us.org/ skechers boots
ronald님의 댓글
ronald 작성일
![]() 비밀글 입니다.
비밀글 입니다.
david님의 댓글
david 작성일
MCM Bags http://www.mcmbags.us/
Fila Sneakers http://www.filashoes.co.uk/
Converse All Star http://www.conversecanada.ca/
KD Shoes http://www.kd11.ca/
Champion Clothing http://www.championsweatshirt.us.com/
Birkenstock Sandals http://www.birkenstockoutlet.us/
ED Hardy Jeans http://www.edhardyclothing.us/
Kyrie 5 http://www.kyrie5shoes.us/
Supreme Clothing http://www.supremeshirt.us/
Fila Canada http://www.filacanada.ca/
Pandora Charms http://www.pandora.in.net/
Giuseppe Zanotti Sale http://www.giuseppezanotti.org.uk/
Bape http://www.bapeshirt.us/
Jordan 11 http://www.jordan-11.us/
Vans Trainers http://www.vansoldskool.org.uk/
Vans Shoes Canada http://www.vanscanada.ca/
Air Max 2019 http://www.airmax-2019.us/
Birkenstock http://www.birkenstock-canada.ca/
Vibram Shoes http://www.vibram-fivefingers.us/
Mulberry http://www.mulberryhandbags.us/
Michael Kors Handbags http://www.michaelkors-bags.us/
Adidas Yeezy http://www.yeezy-supply.us/
Fjallraven http://www.fjallraven.in.net/
Fitflop Sale http://www.fitflopshoes.us/
Bape http://www.bapecanada.ca/
Bape http://www.bape-hoodie.us/
Salvatore Ferragamo http://www.ferragamo.in.net/
Nike Kyrie http://www.kyrie5-shoes.us/
Birkenstock Canada http://www.birkenstockcanadasandals.ca/
Adidas Yeezy Boost 350 http://www.yeezyboost350v2.us.com/
Coach Wallet http://www.coach-bags.us/
Red Bottoms http://www.redbottoms.us.com/
Pandora Jewelry http://www.pandoracanadas.ca/
Golden Goose http://www.goldengoose-shoes.us/
Vans Slip On http://www.vansshoesoutlet.us/
Steph Curry http://www.curry5.ca/
Asics Kayano http://www.asicsrunningshoes.us/
Adidas Boost http://www.adidasboost.us/
Nike Air Max http://www.nikeuptempo.us/
Fjallraven Kanken http://www.fjallraven-canada.ca/
Fjallraven Bags http://www.fjallraven-kanken.us.org/
North Face Coat http://www.northfacejacket.us.org/
Supreme Shoes http://www.supremes.us.org/
Pandora http://www.pandorarings.us/
Puma Rihanna http://www.pumacanada.ca/
Supreme Shirt http://www.supreme-canada.ca/
Harden Vol 3 http://www.hardenvol3.us/
Birkenstock Sale http://www.birkenstock-sale.us/
Adidas Outlet http://www.adidas-outlet.ca/
Burberry http://www.burberrybagsuk.co.uk/
Asics Running Shoes http://www.asicsoutlet.us/
Swarovski Crystal http://www.swarovskijewelry.us/
Pandora Rings http://www.pandoraus.us/
Fila Shoes http://www.fila.in.net/
New Jordans http://www.jordanshoes.ca/
Air Max 2019 http://www.airmax2019.us/
Ecco Shoes For Women http://www.eccoshoessandals.us/
Christian Louboutin http://www.louboutintrainers.co.uk/
Air Max 90 http://www.nikeairmax-uk.co.uk/
Pandora Earrings http://www.pandoraofficialsite.us/
Red Bottoms http://www.redbottomsshoes.us/
Salomon Gtx http://www.salomon-boots.us/
Polo Ralph Lauren Canada http://www.polo-ralphlauren.ca/
Converse All Star http://www.converses.us/
Longchamp http://www.longchampbags-outlet.us/
Longchamp Backpack http://www.longchampbackpack.us/
Fitflop Sandals http://www.fitflop.org.uk/
Ferragamo http://www.ferragamocanada.ca/
Lebron http://www.lebron-16.us.org/
Bvlgari Bracelet http://www.bvlgaris.us/
Off White T Shirt http://www.offwhites.us/
Off White http://www.offwhitecanada.ca/
Champion Hoodie http://www.champion-canada.ca/
Balenciaga Bags http://www.balenciagashoes.ca/
Calvin Klein Underwear http://www.calvinklein.org.uk/
Karen Millen Sale http://www.karen-millen.co.uk/
Balenciaga Sneakers http://www.balenciagasneakers.us/
Nike Outlet http://www.nikeshoxwomen.us/
Goyard Canada http://www.goyardcanada.ca/
Birkenstock http://www.birkenstocksandalssale.us/
Balenciaga Trainers http://www.balenciagas.us/
Vibram http://www.vibram.us.org/
Adidas Canada http://www.adidasyeezy.ca/
Fjallraven Kanken http://www.fjallraven.us.org/
Skechers Boots http://www.skechersoutlet.us/
Pandora Canada http://www.pandoracanadarings.ca/
Balenciaga http://www.balenciaga-sneakers.us.org/
Kate Spade Bags http://www.katespadecanada.ca/
Polo Ralph Lauren Outlet http://www.ralphlaurenusa.us/
Ralph Lauren Outlet http://www.ralphlauren-polo.us/
Nike Shoes http://www.airmax-720.us/
Nike Air Max 95 http://www.airmax-270.co.uk/
Jimmy Choo Boots http://www.jimmychooheels.us/
Nike Air Max http://www.nikecanadashoes.ca/
Supreme Shirt http://www.supremehoodie.co.uk/
Asics Gel Nimbus http://www.asicscanada.ca/
Champion Hoodie http://www.championhoodie.co.uk/
Kate Spade Bags http://www.katespade-purses.us.com/
Vans Shoes http://www.vansslipon.us/
Giuseppe Shoes http://www.giuseppeshoes.us/
Off White http://www.off-white.us.org/
Christian Louboutin http://www.louboutinredbottoms.us/
Golden Goose Superstar http://www.goldengoosesneakers.co.uk/
Red Bottom Shoes http://www.redbottomlouboutinshoes.us/
Goyard Handbags http://www.goyard-bags.us/
Hydro Flask http://www.hydro-flask.us/
Polo Ralph Lauren http://www.ralph-laurencanada.ca/
Hydro Flask 40 OZ http://www.hydroflask.us.org/
Ultra Boost http://www.adidasultraboost.us.com/
Michael Kors Handbags http://www.michaelkorspurse.us/
Kate Spade Outlet http://www.katespadebags.ca/
Air Jordan http://www.jordan11.org.uk/
Christian Louboutin http://www.christianlouboutin-shoes.us/
Converse http://www.converse-uk.co.uk/
Fitflop Sandals http://www.fitflopsandals.us/
Fjallraven http://www.fjallraven.us.com/
Yezzys http://www.yeezytrainers.co.uk/
Balenciaga Shoes http://www.balenciagatrainers.co.uk/
Fjallraven Kanken Backpack http://www.fjallravenkanken.us.com/
Fjallraven http://www.fjallraven.org.uk/
KD 10 http://www.kd-11.us.org/
Pandora Jewelry http://www.pandorajewelrystore.us/
Coach http://www.coachbags.ca/
Yeezy 750 http://www.adidasnmdwomens.us/
Golden Goose Sale http://www.goldengoosesneakers.ca/
Bape http://www.bapehoodie.co.uk/
Coach Bags http://www.coachbags.us/
Jimmy Choo Outlet http://www.jimmy-chooshoes.us/
Yeezy http://www.yeezy-boost.co.uk/
Pandora Charms http://www.pandoras.us/
Skechers outlet http://www.skechersshoes-outlet.us/
Longchamp http://www.longchamp-canada.ca/
Fred Perry Shoes http://www.fredperry.us.org/
Golden Goose Sneakers Sale http://www.goldengooses.us.org/
Bape Clothing http://www.bape.org.uk/
Louboutin Shoes http://www.louboutinredbottomshoes.us/
Nike http://www.nikeairmaxoutlet.us/
Jordan Retro 11 http://www.jordanshoesoutlet.us/
Supreme Hoodie http://www.supremeclothings.us.com/
Champion Clothing http://www.championhoodie.us.com/
Mizuno http://www.mizunoshoes.org/
New Balance http://www.newbalanceshoes.us/
Adidas http://www.adidascanadashoes.ca/
Red Bottom Shoes http://www.christianlouboutinredbottoms.us/
Giuseppe Shoes http://www.giuseppeshoes.us.org/
Coach Outlet http://www.coachbags.co.uk/
Bottega Veneta Bags http://www.bottegavenetas.us/
Cartier Ring http://www.cartier.us.org/
Clarks UK http://www.clarksshoes.org.uk/
Birkenstock Shoes http://www.birkenstock-sandals.co.uk/
Nike Air Max http://www.nikeairmaxca.ca/
Pandora Canada http://www.pandoracanada.ca/
Suicoke http://www.suicoke.us/
Salomon http://www.salomons.us/
Karen Millen http://www.karen-millen.us/
Toms http://www.toms-shoes.us/
Karen Millen Sale http://www.karenmillendresses.co.uk/
Aike Air Max http://www.nikeairmax720.us/
Salomon http://www.salomon.in.net/
Birkenstock Shoes http://www.birkenstockuk.org.uk/
Lebron 15 http://www.lebron16.ca/
Coach Purses http://www.coachbagsoutlet.us/
Curry 5 http://www.curry5shoes.us.org/
Adidas Superstar http://www.adidas-trainersuk.org.uk/
Mont Blanc Pen http://www.mont-blancpens.us/
jerry님의 댓글
jerry 작성일
Air Max 720 http://www.airmax-720.us/
Christian Louboutin Sneakers http://www.louboutinredbottoms.us/
Red Bottom Shoes http://www.christianlouboutinredbottoms.us/
Louboutin Shoes http://www.christianlouboutin-shoes.us/
Salomon Boots http://www.salomon-boots.us/
Jimmy Choo Heels http://www.jimmy-chooshoes.us/
Kate Spade http://www.katespadebags.ca/
Mont Blanc Pens http://www.mont-blancpens.us/
Pandora Rings http://www.pandoracanadarings.ca/
Birkenstock Sale http://www.birkenstock-sandals.co.uk/
Golden Goose Sneakers Sale http://www.goldengoose-shoes.us/
Converse Canada http://www.conversecanada.ca/
Fjallraven Kanken Backpack http://www.fjallraven.us.com/
Balenciaga Shoes http://www.balenciagashoes.ca/
Pandora Charms http://www.pandora.in.net/
Fjallraven Bags http://www.fjallravenkanken.us.com/
Giuseppe Zanotti http://www.giuseppeshoes.us/
Polo Ralph Lauren http://www.ralphlaurenusa.us/
Yeezy http://www.yeezyboost350v2.us.com/
Suicoke Shoes http://www.suicoke.us/
Coach http://www.coach-bags.us/
Adidas Superstar http://www.adidascanadashoes.ca/
Nike Air Max http://www.airmax-2019.us/
New Balance Women http://www.newbalanceshoes.us/
Nike Outlet http://www.nikeshoxwomen.us/
Bape Clothing http://www.bape-hoodie.us/
Louboutin Heels http://www.louboutintrainers.co.uk/
Goyard http://www.goyard-bags.us/
Mulberry Bayswater http://www.mulberryhandbags.us/
Mizuno Running Shoes http://www.mizunoshoes.org/
High Top Vans http://www.vansslipon.us/
Champion Hoodie http://www.champion-canada.ca/
Kate Spade Canada http://www.katespadecanada.ca/
MCM Backpack http://www.mcmbags.us/
Red Bottoms http://www.louboutinredbottomshoes.us/
Michael Kors Handbags http://www.michaelkors-bags.us/
Coach Wallet http://www.coachbags.co.uk/
Converse High Tops http://www.converses.us/
Vans http://www.vanscanada.ca/
Nike http://www.nikecanadashoes.ca/
Bape Shirt http://www.bapehoodie.co.uk/
Adidas Yeezy http://www.adidasyeezy.ca/
Air Max 95 http://www.airmax2019.us/
Pandora Canada http://www.pandoracanada.ca/
Nike Air More Uptempo http://www.nikeuptempo.us/
Yeezy http://www.yeezy-boost.co.uk/
Salomon http://www.salomons.us/
Kyrie 4 http://www.kyrie5-shoes.us/
Giuseppe Shoes http://www.giuseppezanotti.org.uk/
Vans Shoes http://www.vansoldskool.org.uk/
Fila http://www.filacanada.ca/
Adidas Yeezy http://www.adidasboost.us/
Pandora http://www.pandoraus.us/
Fila Shoes http://www.fila.in.net/
Golden Goose http://www.goldengooses.us.org/
Vibram Five Fingers http://www.vibram.us.org/
Hydro Flask http://www.hydro-flask.us/
Pandora Bracelet http://www.pandoras.us/
Fjallraven http://www.fjallraven.in.net/
Harden Vol 3 http://www.hardenvol3.us/
Pandora Charms http://www.pandorarings.us/
Champion Sweatshirt http://www.championhoodie.us.com/
Fjallraven Kanken Backpack http://www.fjallraven.us.org/
Adidas Trainers http://www.adidas-trainersuk.org.uk/
Bottega Veneta Bags http://www.bottegavenetas.us/
Giuseppe Shoes http://www.giuseppeshoes.us.org/
Lebron Shoes http://www.lebron16.ca/
Curry 6 http://www.curry5shoes.us.org/
Bape Shark Hoodie http://www.bapecanada.ca/
Birkenstock http://www.birkenstockuk.org.uk/
Champion T Shirt http://www.championhoodie.co.uk/
ED Hardy Dress http://www.edhardyclothing.us/
Off White Hoodie http://www.offwhitecanada.ca/
Birkenstock Outlet http://www.birkenstock-sale.us/
Ralph Lauren http://www.polo-ralphlauren.ca/
Polo Ralph Lauren http://www.ralphlauren-polo.us/
Asics http://www.asicscanada.ca/
Longchamp Outlet http://www.longchampbags-outlet.us/
Champion Hoodie http://www.championsweatshirt.us.com/
Longchamp Backpack http://www.longchampbackpack.us/
Balenciaga http://www.balenciagatrainers.co.uk/
Fjallraven Sale http://www.fjallraven.org.uk/
Karen Millen UK http://www.karen-millen.co.uk/
Fila High Tops http://www.filashoes.co.uk/
Air Jordan http://www.jordan11.org.uk/
Pandora Rings http://www.pandoraofficialsite.us/
Karen Millen Outlet http://www.karenmillendresses.co.uk/
Karen Millen Clothing http://www.karen-millen.us/
Birkenstock Outlet http://www.birkenstockoutlet.us/
Nike Air Max http://www.nikeairmax-uk.co.uk/
Calvin Klein Bikini http://www.calvinklein.org.uk/
Coach Canada http://www.coachbags.ca/
Skechers Boots http://www.skechersshoes-outlet.us/
Yeezy 350 http://www.yeezytrainers.co.uk/
Louboutin Shoes http://www.redbottoms.us.com/
Golden Goose Sneakers http://www.goldengoosesneakers.ca/
Ecco Golf Shoes http://www.eccoshoessandals.us/
Jimmy Choo Sandals http://www.jimmychooheels.us/
Supreme Shirt http://www.supremehoodie.co.uk/
Balenciagas http://www.balenciagasneakers.us/
Yeezy Shoes http://www.yeezy-supply.us/
Adidas Shoes http://www.adidas-outlet.ca/
Off White Shoes http://www.off-white.us.org/
Nike Air Max 95 http://www.airmax-270.co.uk/
Supreme http://www.supremeclothings.us.com/
Fjallraven http://www.fjallraven-kanken.us.org/
Fred Perry Polo http://www.fredperry.us.org/
Five Finger Shoes http://www.vibram-fivefingers.us/
Asics Shoes http://www.asicsrunningshoes.us/
Michael Kors Wallet http://www.michaelkorspurse.us/
Pandora http://www.pandorajewelrystore.us/
Off White http://www.offwhites.us/
Jordan Shoes http://www.jordanshoesoutlet.us/
Asics Gel http://www.asicsoutlet.us/
Goyard Bags http://www.goyardcanada.ca/
Fjallraven Kanken Backpack http://www.fjallraven-canada.ca/
Swarovski Bracelet http://www.swarovskijewelry.us/
Birkenstock Sandals http://www.birkenstocksandalssale.us/
Jordan Shoes http://www.jordanshoes.ca/
Fitflops Clearance http://www.fitflopsandals.us/
Golden Goose Superstar http://www.goldengoosesneakers.co.uk/
Nike Air Max 270 http://www.nikeairmaxoutlet.us/
Hydro Flask Sale http://www.hydroflask.us.org/
KD Shoes http://www.kd11.ca/
Fitflop http://www.fitflop.org.uk/
Nike KD http://www.kd-11.us.org/
North Face Outlet http://www.northfacejacket.us.org/
Supreme Clothing http://www.supreme-canada.ca/
Bvlgari http://www.bvlgaris.us/
Christian Louboutin Heels http://www.redbottomsshoes.us/
Supreme Sweatshirt http://www.supremes.us.org/
Fitflops Clearance http://www.fitflopshoes.us/
Coach Handbags http://www.coachbagsoutlet.us/
Aike Air Max http://www.nikeairmax720.us/
Toms Boots http://www.toms-shoes.us/
Balenciaga Bags http://www.balenciagas.us/
Kyrie 5 http://www.kyrie5shoes.us/
Birkenstock http://www.birkenstockcanadasandals.ca/
Clarks UK http://www.clarksshoes.org.uk/
Red Bottoms http://www.redbottomlouboutinshoes.us/
Salvatore http://www.ferragamo.in.net/
Longchamp Canada http://www.longchamp-canada.ca/
Coach Bags http://www.coachbags.us/
A Bathing Ape http://www.bape.org.uk/
Skechers http://www.skechersoutlet.us/
Ferragamo Canada http://www.ferragamocanada.ca/
Pandora Canada http://www.pandoracanadas.ca/
Cartier Bracelet http://www.cartier.us.org/
Supreme Clothing http://www.supremeshirt.us/
Bape http://www.bapeshirt.us/
Adidas Originals Ultra Boost http://www.adidasultraboost.us.com/
Salomon Speedcross 5 http://www.salomon.in.net/
Kate Spade Purses http://www.katespade-purses.us.com/
Burberry http://www.burberrybagsuk.co.uk/
Vans Slip On http://www.vansshoesoutlet.us/
Balenciaga http://www.balenciaga-sneakers.us.org/
Lebron 16 Shoes http://www.lebron-16.us.org/
Birkenstock Sandals http://www.birkenstock-canada.ca/
Jordan Shoes http://www.jordan-11.us/
Converse All Star http://www.converse-uk.co.uk/
Adidas NMD http://www.adidasnmdwomens.us/
Nike Shoes http://www.nikeairmaxca.ca/
Puma Suede http://www.pumacanada.ca/
Curry 5 http://www.curry5.ca/
Polo Ralph Lauren http://www.ralph-laurencanada.ca/
xueqin69님의 댓글
xueqin69 작성일
http://www.moncler-uk.co.uk/ moncler coat
http://www.filas.us.org/ fila sneakers
http://www.ultra-boost.ca/ adidas ultra boost
http://www.goyard.org.uk/ goyard tote
http://www.doudoune-moncler.fr/ moncler femme
http://www.goyardbag.us.com/ goyard wallet
http://www.giuseppezanottisneakers.us/ giuseppe zanotti sneakers
http://www.jordan-retro11.us.com/ jordan retro
http://www.philipppleinoutlet.us/ philipp plein outlet
http://www.skechers.in.net/ skechers sandals
http://www.burberry--scarf.us.com/ burberry outlet
http://www.northfacejacketoutlets.us.com/ north face coats
http://www.nikeairmax97.co.uk/ air max 97
http://www.balenciagas.ca/ balenciaga
http://www.vapormaxs.us.com/ nike vapormax
http://www.ferragamoshoess.us.com/ ferragamo shoes
http://www.monclers.us.com/ moncler jacket mens
http://www.chaussure-yeezy.fr/ yeezy boost 350 v2
http://www.salomonspeedcross3.us.com/ salomon speedcross 3
http://www.yeezy--shoes.co.uk/ yeezy boost 350 v2
http://www.yeezy-750.us/ yeezy 750
http://www.pandora--jewelry.us.org/ pandora bracelet
http://www.hermesbirkin-handbags.us.com/ Hermes Wallets
http://www.monclerjacketwomens.us.com/ moncler jacket womens
http://www.salomonshoes.co.uk/ salomon boots
http://www.airmax270.co.uk/ nike air max
http://www.salomonboots.co.uk/ salomon shoes
http://www.nike-canada.ca/ nike shoes
http://www.skechers-shoes.ca/ skechers canada
http://www.balenciaga.us.org/ balenciaga sneakers
http://www.louboutinredbottoms.us.com/ red bottoms
http://www.nikeairvapormaxflyknit.us.com/ vapormax
http://www.nikeairmax-90.us.com/ Nike Air Max 90
http://www.adidasoriginalsultraboost.us.com/ ultra boost uncaged
http://www.chaussuresalomon.fr/ salomon speedcross
http://www.longchampbag.us.com/ longchamp backpack
http://www.fitflop-shoes.ca/ fitflop
http://www.bracelet-pandora.fr/ pandora
http://www.coachbags-outlet.us.com/ coach purses
http://www.yeezys.fr/ yeezy
http://www.katespades.ca/ kate spade outlet
http://www.goldengoosesneakerssale.us/ golden goose
http://www.louboutin-shoesuk.co.uk/ christian louboutin uk
http://www.jordan11.co.uk/ air jordan
http://www.pandora-charmsjewelry.us.com/ pandora earrings
http://www.kd11shoes.us/ kd shoes
http://www.monclers.ca/ moncler coat
http://www.fjallravenkanken-backpack.us/ fjallraven backpack
http://www.vans--shoes.us.com/ vans
http://www.redbottomslouboutinshoes.us.com/ red bottom shoes
http://www.jordan-11.fr/ jordan
http://www.yeezy-950.us/ yeezy 750
http://www.pandoracanadacharms.ca/ pandora charms
http://www.adidasyeezyshoes.co.uk/ yeezy boost
http://www.mizunos.us/ mizuno shoes
http://www.fitflops-sale.us.com/ fitflop shoes
http://www.burberrys.org.uk/ burberry backpack
http://www.jordans11shoes.us.com/ jordan 11
http://www.adidasnmdrunnerr1.us.com/ adidas ultra boost
http://www.northface-jacket.us.com/ north face outlet
http://www.ed-hardys.us.com/ ed hardy shirt
http://www.charmsstore.us/ pandora charms
http://www.salomonshoes.ca/ salomon xa pro 3d
http://www.fjallravenkankens.us/ fjallraven
http://www.uggsforwomen.us/ ugg boots
http://www.monclerjacket.org.uk/ moncler jacket womens
http://www.pandora-jewelrys.ca/ pandora charm
http://www.moncler-coat.us.com/ moncler sale
http://www.yeezy-500.us/ yeezy
http://www.giuseppezanottis.us/ giuseppe zanotti sneakers
http://www.pandorajewelryrings.us.com/ pandora bracelet
http://www.fitflopsshoes.us.com/ fitflop
http://www.air-max.us/ nike
http://www.katespadepurses.us.com/ kate spade purses
http://www.pandorauk.us.com/ pandora charms
http://www.jordan11shoes.us.com/ jordan 11
http://www.airmax-2019.us.com/ air max 2019
http://www.birkenstock-sandals.ca/ birkenstock sandals
http://www.adidasyeezy-350.us.com/ yeezy boost 350
http://www.james-hardenshoes.us.com/ harden vol 1
http://www.goyards.ca/ goyard
http://www.nmds.ca/ nmd
http://www.adidastrainers-uk.co.uk/ adidas
http://www.goyardhandbags.us/ goyard
http://www.nike-airmax270.us.com/ air max
http://www.katespadebags.us.com/ kate spade wallet
http://www.adidasyeezyboost.fr/ yeezy boost 350 v2
http://www.adidaschaussure.fr/ adidas superstar
http://www.pandoras.in.net/ pandora bracelet
http://www.nikeoffwhite.us.com/ off white
http://www.chaussure-adidas.fr/ chaussure adidas
http://www.christianlouboutins.fr/ louboutin homme
http://www.yeezyshoes.ca/ yeezy
http://www.pandora-bracelet.fr/ bague pandora
http://www.jordan11.us.com/ jordan shoes
http://www.jordan11spacejams.us.com/ jordan retro 12
http://www.nike-airmax-2018.us.com/ air max 2018
http://www.goyard.in.net/ goyard bag
http://www.kd10-shoes.us.com/ kd 9
http://www.adidas--yeezy.co.uk/ yeezy
http://www.nikeoffwhiteshoes.us/ off white shoes
http://www.lebron15-shoes.us.com/ lebron 14
http://www.adidas-yeezy-shoes.us.com/ Yeezy Boost 350 V2
http://www.mizuno-shoes.us/ mizuno
http://www.goldengoosesale.us/ golden goose shoes
http://www.adidas-ultraboost.us.com/ ultra boost
http://www.long-champs.us.com/ longchamp bag
http://www.airmax90shoes.us.com/ nike air max 95
http://www.nikeairmax-2019.us.com/ nike air max 2019
http://www.cartier-bracelet.us.com/ cartier bracelet
http://www.balenciagas-sneakers.us.com/ balenciaga shoes
http://www.jordan--shoes.us.com/ air jordan
http://www.nikeair-max90.co.uk/ nike air max 90
http://www.bijoux-pandora.fr/ bague pandora
http://www.salvatore-ferragamo.us.com/ ferragamo shoes
http://www.celines.us.com/ celine wallet
http://www.redbottoms-shoes.us.org/ louboutin shoes
http://www.airjordan11spacejam.us.com/ air jordan 11 space jam
http://www.longchampbackpack.us.com/ longchamp
http://www.nmd.us.org/ adidas nmd
http://www.jordan11.ca/ jordan shoes
http://www.ultraboost-uncaged.us/ adidas boost
http://www.nikeairmax.fr/ nike
http://www.uggslippers.ca/ ugg boots
http://www.yeezyboost-350v2.fr/ yeezy boost 350
http://www.nike-airmax.ca/ air max 97
http://www.bijouxpandoras.fr/ bracelet pandora
http://www.nike-vapormax.ca/ nike vapormax
http://www.monclerjacket.us/ moncler sale
http://www.fila-shoes.us/ fila mens shoes
http://www.polo-ralphlauren-outlet.us.com/ polo
http://www.katespade-bags.us/ kate spade bags
http://www.golden-goosesneakers.us.com/ golden goose shoes
http://www.eccoshoesoutlets.us.com/ ecco mens shoes
http://www.airmax95.co.uk/ nike air max 95 mens
http://www.adidas-nmd.fr/ Adidas Nmd
http://www.pandoras-jewelrys.us.com/ pandora
http://www.yeezyboost350shoes.us.com/ yeezy boost 350 v2
http://www.nikeairmax270.org.uk/ nike air max 270
http://www.lebron-16shoes.us/ lebron 15
http://www.pandorajewelryscharms.us.com/ pandora Charms
http://www.monclers.uk/ moncler sale
http://www.chaussurelouboutinpascher.fr/ chaussure louboutin
http://www.chaussuresskechers.fr/ chaussures skechers
http://www.katespades.co.uk/ kate spade handbags
http://www.christianlouboutinredbottoms.us.com/ louboutin
http://www.curry-5shoes.us/ currys
http://www.adidaseqt.us.org/ adidas originals eqt
http://www.pandora-jewelrysale.us.com/ pandora bracelet
http://www.nikeairmax270.ca/ nike off white
http://www.airmax90.fr/ nike air max
http://www.lebron16-shoes.us/ nike lebron
http://www.red-bottoms.org.uk/ louboutin heels
http://www.air-max-270.us.com/ air max 270
http://www.nikelebron15.us.com/ nike lebron
http://www.zxflux.us/ zx flux
http://www.kate-spadepurses.us/ kate spade
http://www.nike--shoes.co.uk/ nike outlet
http://www.nikeairmax90.ca/ air max
http://www.philipppleins.us/ philipp plein
http://www.yeezy.in.net/ adidas yeezy
http://www.red-bottoms.us.org/ christian louboutin
http://www.salomon-chaussures.fr/ salomon speedcross 4
http://www.skechers-shoe.us.com/ skechers shoes
http://www.redbottom-shoes.co.uk/ christian louboutin
http://www.birkenstocksandalssale.us.com/ birkenstock sandals
http://www.salomon.us.org/ salomon xa pro 3d
xiaodai79님의 댓글
xiaodai79 작성일
http://www.salomonshoes.ca/ salomon boots
http://www.adidas-nmd.fr/ Chaussure Adidas
http://www.louboutinredbottoms.us.com/ louboutin shoes
http://www.pandorajewelryscharms.us.com/ pandora jewelry official site
http://www.skechers-shoes.ca/ skechers go walk
http://www.balenciagas-sneakers.us.com/ balenciaga
http://www.balenciaga.us.org/ balenciagas
http://www.kate-spadepurses.us/ kate spade outlet
http://www.salomonshoes.co.uk/ salomon
http://www.uggslippers.ca/ ugg boots
http://www.long-champs.us.com/ longchamp tote
http://www.fitflops-sale.us.com/ fitflop shoes
http://www.charmsstore.us/ pandora rings
http://www.pandora-charmsjewelry.us.com/ pandora bracelet
http://www.giuseppezanottis.us/ giuseppe shoes
http://www.yeezy-750.us/ yeezy shoes
http://www.airmax95.co.uk/ nike air max 95 mens
http://www.redbottomslouboutinshoes.us.com/ christian louboutin
http://www.yeezys.fr/ yeezy
http://www.adidas--yeezy.co.uk/ yeezy 350
http://www.vans--shoes.us.com/ vans slip on
http://www.goyard.org.uk/ goyard
http://www.adidasoriginalsultraboost.us.com/ ultra boost
http://www.yeezyshoes.ca/ adidas yeezy
http://www.nike-vapormax.ca/ nike air vapormax flyknit
http://www.ferragamoshoess.us.com/ salvatore ferragamo shoes
http://www.fila-shoes.us/ fila mens shoes
http://www.airmax90shoes.us.com/ nike air max
http://www.nike-airmax.ca/ nike air max 270
http://www.goyards.ca/ goyard canada
http://www.katespadepurses.us.com/ kate spade handbags
http://www.nikeairmax270.org.uk/ nike air max 90
http://www.jordan11spacejams.us.com/ jordan shoes
http://www.nike-airmax270.us.com/ nike air max
http://www.james-hardenshoes.us.com/ harden vol 2
http://www.katespadebags.us.com/ kate spade
http://www.katespade-bags.us/ kate spade purses
http://www.coachbags-outlet.us.com/ coach outlet
http://www.pandoracanadacharms.ca/ pandora rings
http://www.nikeairmax97.co.uk/ nike shoes
http://www.nikeairmax-2019.us.com/ air max 2019
http://www.monclers.us.com/ moncler
http://www.nikeoffwhite.us.com/ nike off white
http://www.giuseppezanottisneakers.us/ giuseppe
http://www.filas.us.org/ fila sneakers
http://www.goldengoosesale.us/ golden goose sneakers
http://www.kd10-shoes.us.com/ kd 9
http://www.christianlouboutinredbottoms.us.com/ christian louboutin
http://www.monclerjacket.org.uk/ moncler
http://www.bijoux-pandora.fr/ bracelet pandora
http://www.hermesbirkin-handbags.us.com/ Hermes Belts
http://www.yeezy-500.us/ yeezy
http://www.redbottoms-shoes.us.org/ red bottom shoes
http://www.nikeairmax270.ca/ nike off white
http://www.chaussure-adidas.fr/ chaussure adidas
http://www.chaussuresalomon.fr/ salomon speedcross
http://www.airmax90.fr/ nike air max
http://www.jordan11.ca/ new jordans
http://www.monclerjacketwomens.us.com/ moncler jacket
http://www.yeezy--shoes.co.uk/ yeezy shoes
http://www.zxflux.us/ zx flux
http://www.chaussuresskechers.fr/ skechers homme
http://www.christianlouboutins.fr/ louboutin femme
http://www.doudoune-moncler.fr/ moncler homme
http://www.longchampbackpack.us.com/ longchamp bag
http://www.jordan-retro11.us.com/ jordan retro
http://www.fjallravenkankens.us/ fjallraven kanken backpack
http://www.salomon.us.org/ salomon boots
http://www.yeezyboost350shoes.us.com/ yeezy boost 350
http://www.nikeairmax.fr/ air max
http://www.pandora-bracelet.fr/ bracelet pandora
http://www.adidasyeezyboost.fr/ yeezy
http://www.louboutin-shoesuk.co.uk/ christian louboutin uk
http://www.nikeairvapormaxflyknit.us.com/ nike air max 90
http://www.birkenstocksandalssale.us.com/ birkenstock sandals
http://www.bracelet-pandora.fr/ bague pandora
http://www.moncler-uk.co.uk/ moncler coat
http://www.monclers.uk/ moncler jacket mens
http://www.burberrys.org.uk/ burberry
http://www.salomonspeedcross3.us.com/ salomon xa pro 3d
http://www.ultra-boost.ca/ adidas originals ultra boost
http://www.moncler-coat.us.com/ moncler
http://www.pandora-jewelrys.ca/ pandora earrings
http://www.fitflopsshoes.us.com/ fitflop sale
http://www.adidas-ultraboost.us.com/ yeezy boost 350
http://www.nmds.ca/ adidas originals nmd
http://www.vapormaxs.us.com/ air vapormax
http://www.nikeairmax-90.us.com/ Nike Air Max 90
http://www.jordan-11.fr/ jordan 11
http://www.nike-airmax-2018.us.com/ air max 2018
http://www.katespades.co.uk/ kate spade
http://www.goyard.in.net/ goyard handbags
http://www.skechers.in.net/ skechers
http://www.yeezyboost-350v2.fr/ yeezy boost
http://www.ultraboost-uncaged.us/ adidas originals ultra boost
http://www.mizuno-shoes.us/ mizuno
http://www.air-max.us/ nike air max plus
http://www.cartier-bracelet.us.com/ cartier jewelry
http://www.ed-hardys.us.com/ ed hardy jeans
http://www.goyardhandbags.us/ goyard tote
http://www.adidaschaussure.fr/ adidas
http://www.chaussure-yeezy.fr/ yeezy boost 350
http://www.fitflop-shoes.ca/ fitflop
http://www.pandoras-jewelrys.us.com/ pandora bracelet
http://www.nikeoffwhiteshoes.us/ off white
http://www.northface-jacket.us.com/ north face
http://www.nikeairmax90.ca/ air max 90
http://www.jordan11.us.com/ jordan
http://www.jordan11.co.uk/ air jordan
http://www.airmax270.co.uk/ nike air max 270
http://www.jordan--shoes.us.com/ new jordans
http://www.nike--shoes.co.uk/ nike air max 270
http://www.katespades.ca/ kate spade
http://www.goyardbag.us.com/ goyard bag
http://www.skechers-shoe.us.com/ skechers
http://www.pandorajewelryrings.us.com/ pandora necklace
http://www.adidasnmdrunnerr1.us.com/ adidas ultra boost
http://www.salvatore-ferragamo.us.com/ ferragamo
http://www.yeezy-950.us/ yeezy 750
http://www.philipppleinoutlet.us/ philipp plein t shirt
http://www.pandoras.in.net/ pandora jewelry
http://www.northfacejacketoutlets.us.com/ north face coats
http://www.pandora-jewelrysale.us.com/ pandora jewelry official site
http://www.adidaseqt.us.org/ adidas eqt
http://www.lebron16-shoes.us/ lebron james shoes
http://www.uggsforwomen.us/ ugg
http://www.nmd.us.org/ adidas originals nmd
http://www.bijouxpandoras.fr/ bijoux pandora
http://www.redbottom-shoes.co.uk/ louboutin heels
http://www.chaussurelouboutinpascher.fr/ louboutin femme
http://www.polo-ralphlauren-outlet.us.com/ ralph lauren
http://www.yeezy.in.net/ yeezy shoes
http://www.kd11shoes.us/ kd 11
http://www.burberry--scarf.us.com/ burberry scarf
http://www.adidasyeezyshoes.co.uk/ yeezy
http://www.red-bottoms.org.uk/ christian louboutin
http://www.adidastrainers-uk.co.uk/ adidas
http://www.nikelebron15.us.com/ lebron james shoes
http://www.golden-goosesneakers.us.com/ golden goose
http://www.fjallravenkanken-backpack.us/ fjallraven backpack
http://www.airjordan11spacejam.us.com/ air jordan 11 space jam
http://www.jordans11shoes.us.com/ jordan 11
http://www.mizunos.us/ mizuno shoes
http://www.adidasyeezy-350.us.com/ adidas yeezy
http://www.curry-5shoes.us/ currys
http://www.jordan11shoes.us.com/ jordan 11 space jam
http://www.adidas-yeezy-shoes.us.com/ Yeezy Boost 350 V2
http://www.salomonboots.co.uk/ salomon
http://www.longchampbag.us.com/ longchamp le pliage
http://www.lebron-16shoes.us/ lebron 16
http://www.air-max-270.us.com/ nike air max 270
http://www.nikeair-max90.co.uk/ nike air max 95
http://www.balenciagas.ca/ balenciaga canada
http://www.monclerjacket.us/ moncler coat
http://www.monclers.ca/ moncler sale
http://www.lebron15-shoes.us.com/ lebron shoes
http://www.nike-canada.ca/ nike store
http://www.salomon-chaussures.fr/ salomon
http://www.goldengoosesneakerssale.us/ golden goose sneakers
http://www.philipppleins.us/ philipp plein shoes
http://www.red-bottoms.us.org/ red bottoms
http://www.birkenstock-sandals.ca/ birkenstock shoes
http://www.airmax-2019.us.com/ air max 270
http://www.celines.us.com/ celine purse
http://www.eccoshoesoutlets.us.com/ ecco boots
http://www.pandorauk.us.com/ pandora
http://www.pandora--jewelry.us.org/ pandora jewelry
david님의 댓글
david 작성일
Fitflops Clearance http://www.fitflopsandals.us/
Nike Lebron http://www.lebron16.ca/
Vans Slip On http://www.vansoldskool.org.uk/
Goyard Bags http://www.goyardcanada.ca/
Lauren Ralph Lauren http://www.ralphlauren-polo.us/
Nike Air Max 97 http://www.airmax-720.us/
Jimmy Choo Shoes http://www.jimmy-chooshoes.us/
Kate Spade http://www.katespadecanada.ca/
Converse Sneakers http://www.converses.us/
Off White Hoodie http://www.off-white.us.org/
Bape Hoodie http://www.bapehoodie.co.uk/
Supreme Sweatshirt http://www.supremehoodie.co.uk/
Birkenstock Sale http://www.birkenstockuk.org.uk/
KD 11 http://www.kd-11.us.org/
Ferragamo Canada http://www.ferragamocanada.ca/
Fila http://www.filacanada.ca/
Pandora Bracelet http://www.pandoras.us/
New Balance 574 http://www.newbalanceshoes.us/
Fjallraven Backpack http://www.fjallravenkanken.us.com/
Fred Perry http://www.fredperry.us.org/
Yeezy 350 http://www.yeezyboost350v2.us.com/
hampion Clothing http://www.championhoodie.co.uk/
Asics Kayano http://www.asicsrunningshoes.us/
Fjallraven Kanken Backpack http://www.fjallraven-canada.ca/
Puma Rihanna http://www.pumacanada.ca/
Ultra Boost http://www.adidasultraboost.us.com/
Jordan Retro 11 http://www.jordan-11.us/
Fila Shoes Womens http://www.fila.in.net/
Nike Air Max http://www.nikeairmax-uk.co.uk/
Swarovski Jewelry http://www.swarovskijewelry.us/
Bottega Veneta http://www.bottegavenetas.us/
Balenciagas http://www.balenciagasneakers.us/
Michael Kors Handbags http://www.michaelkorspurse.us/
Fjallraven Kanken Backpack http://www.fjallraven.us.com/
Pandora Rings http://www.pandoracanadas.ca/
Christian Louboutin http://www.redbottomsshoes.us/
Five Finger Shoes http://www.vibram.us.org/
High Top Vans http://www.vansslipon.us/
Jimmy Choo Shoes http://www.jimmychooheels.us/
Kate Spade http://www.katespadebags.ca/
Cartier Bracelet http://www.cartier.us.org/
Fjallraven Bags http://www.fjallraven-kanken.us.org/
Golden Goose Shoes http://www.goldengooses.us.org/
Adidas NMD http://www.adidasboost.us/
Fjallraven Kanken http://www.fjallraven.us.org/
Nike Air Max http://www.nikeairmaxoutlet.us/
Longchamp Outlet http://www.longchampbags-outlet.us/
Nike Shox http://www.nikeshoxwomen.us/
Supreme http://www.supremeclothings.us.com/
Louboutin Heels http://www.louboutintrainers.co.uk/
Fjallraven http://www.fjallraven.org.uk/
Balenciaga Shoes http://www.balenciaga-sneakers.us.org/
Hydro Flask Sale http://www.hydro-flask.us/
Yeezy Boost http://www.adidasyeezy.ca/
Air Max 270 http://www.airmax-2019.us/
Mulberry Purse http://www.mulberryhandbags.us/
Longchamp Bags http://www.longchamp-canada.ca/
Yeezy Trainers http://www.yeezytrainers.co.uk/
Pandora Charms http://www.pandoracanadarings.ca/
Birkenstock Sale http://www.birkenstock-sale.us/
Birkenstock Outlet http://www.birkenstocksandalssale.us/
Air Max 2019 http://www.airmax2019.us/
Ecco http://www.eccoshoessandals.us/
Supreme http://www.supremes.us.org/
Off White Shoes http://www.offwhitecanada.ca/
Fitflop UK http://www.fitflop.org.uk/
Nike Air Max http://www.nikeuptempo.us/
Vibram 5 Fingers http://www.vibram-fivefingers.us/
Ralph Lauren USA http://www.ralphlaurenusa.us/
Longchamp Tote http://www.longchampbackpack.us/
Bape Sweatshirt http://www.bape.org.uk/
Giuseppe Shoes http://www.giuseppeshoes.us/
Michael Kors Outlet http://www.michaelkors-bags.us/
Vans Shoes http://www.vansshoesoutlet.us/
Nike Air Max 97 http://www.airmax-270.co.uk/
Champion Clothing http://www.championhoodie.us.com/
Ferragamo http://www.ferragamo.in.net/
Birkenstock http://www.birkenstockcanadasandals.ca/
Red Bottoms http://www.louboutinredbottoms.us/
Golden Goose Sneakers http://www.goldengoosesneakers.co.uk/
Golden Goose http://www.goldengoose-shoes.us/
Jordan Shoes http://www.jordan11.org.uk/
Giuseppe http://www.giuseppezanotti.org.uk/
Burberry http://www.burberrybagsuk.co.uk/
Adidas Yeezy http://www.yeezy-supply.us/
Nike Shoes http://www.nikecanadashoes.ca/
Nike http://www.nikeairmaxca.ca/
Yeezy Boost http://www.yeezy-boost.co.uk/
Coach Bags http://www.coachbags.co.uk/
Skechers Boots http://www.skechersoutlet.us/
Steph Curry Shoes http://www.curry5shoes.us.org/
Balenciagas http://www.balenciagashoes.ca/
Lauren Ralph Lauren http://www.ralph-laurencanada.ca/
Skechers outlet http://www.skechersshoes-outlet.us/
Bape Shirt http://www.bapeshirt.us/
Curry 5 http://www.curry5.ca/
North Face Jacket http://www.northfacejacket.us.org/
Polo Ralph Lauren http://www.polo-ralphlauren.ca/
Bape http://www.bapecanada.ca/
Lebron 16 Shoes http://www.lebron-16.us.org/
Fjallraven Backpack http://www.fjallraven.in.net/
Fitflop http://www.fitflopshoes.us/
Clarks http://www.clarksshoes.org.uk/
Supreme Shirt http://www.supremeshirt.us/
Kate Spade Purses http://www.katespade-purses.us.com/
Karen Millen UK http://www.karen-millen.co.uk/
Coach Bags http://www.coachbags.ca/
Harden Shoes http://www.hardenvol3.us/
Birkenstock Outlet http://www.birkenstockoutlet.us/
Coach Purses http://www.coachbags.us/
Red Bottoms http://www.redbottomlouboutinshoes.us/
Pandora Bracelet http://www.pandoraus.us/
CK Underwear http://www.calvinklein.org.uk/
Toms Womens Shoes http://www.toms-shoes.us/
Salomon Xa Pro 3d http://www.salomon-boots.us/
ED Hardy Dress http://www.edhardyclothing.us/
Mont Blanc http://www.mont-blancpens.us/
Adidas Superstar http://www.adidascanadashoes.ca/
Supreme Clothing http://www.supreme-canada.ca/
Aike Air Max 270 http://www.nikeairmax720.us/
Pandora Rings http://www.pandoraofficialsite.us/
Hydro Flask 40 OZ http://www.hydroflask.us.org/
Air Jordan 11 http://www.jordanshoes.ca/
Red Bottoms http://www.redbottoms.us.com/
Champion http://www.championsweatshirt.us.com/
Suicoke http://www.suicoke.us/
Golden Goose Shoes http://www.goldengoosesneakers.ca/
Birkenstock http://www.birkenstock-sandals.co.uk/
KD 10 http://www.kd11.ca/
Champion Clothing http://www.champion-canada.ca/
Coach http://www.coach-bags.us/
Louboutin Shoes http://www.louboutinredbottomshoes.us/
Balenciaga Shoes http://www.balenciagas.us/
Balenciaga Shoes http://www.balenciagatrainers.co.uk/
Off White Sneakers http://www.offwhites.us/
Pandora Charms http://www.pandorarings.us/
Fila Shoes http://www.filashoes.co.uk/
Giuseppe Zanotti Sale http://www.giuseppeshoes.us.org/
Karen Millen Outlet http://www.karen-millen.us/
Coach Handbags http://www.coachbagsoutlet.us/
Bape Shirt http://www.bape-hoodie.us/
Salomon Shoes http://www.salomon.in.net/
Bvlgari Bracelet http://www.bvlgaris.us/
Nike Kyrie http://www.kyrie5-shoes.us/
Birkenstock Shoes http://www.birkenstock-canada.ca/
Converse High Tops http://www.converse-uk.co.uk/
Kyrie 5 Shoes http://www.kyrie5shoes.us/
MCM Purse http://www.mcmbags.us/
New Jordans http://www.jordanshoesoutlet.us/
Pandora Jewelry http://www.pandorajewelrystore.us/
Goyard Bags http://www.goyard-bags.us/
Salomon Shoes http://www.salomons.us/
Red Bottoms http://www.christianlouboutinredbottoms.us/
Adidas Shoes http://www.adidas-outlet.ca/
Vans Shoes http://www.vanscanada.ca/
Pandora Charms http://www.pandora.in.net/
Asics Shoes http://www.asicsoutlet.us/
Asics Canada http://www.asicscanada.ca/
Pandora http://www.pandoracanada.ca/
Christian Louboutin Shoes http://www.christianlouboutin-shoes.us/
Adidas Stan Smith http://www.adidas-trainersuk.org.uk/
Karen Millen Sale http://www.karenmillendresses.co.uk/
Converse All Star http://www.conversecanada.ca/
Yeezy 750 http://www.adidasnmdwomens.us/
Mizuno http://www.mizunoshoes.org/
xiaolei68님의 댓글
xiaolei68 작성일
http://www.goyardhandbags.us/ goyard handbags
http://www.salomonshoes.co.uk/ salomon shoes
http://www.adidasoriginalsultraboost.us.com/ adidas originals ultra boost
http://www.jordan11.us.com/ jordan
http://www.pandora-jewelrys.ca/ pandora rings
http://www.lebron15-shoes.us.com/ lebron james shoes
http://www.nike-airmax-2018.us.com/ air max 2018
http://www.adidas-nmd.fr/ Nmd
http://www.goyardbag.us.com/ goyard bag
http://www.katespade-bags.us/ kate spade handbags
http://www.zxflux.us/ adidas flux
http://www.burberrys.org.uk/ burberry
http://www.fitflop-shoes.ca/ fitflop canada
http://www.nikeairmax90.ca/ air max
http://www.yeezy-950.us/ adidas yeezy
http://www.pandorajewelryrings.us.com/ pandora earrings
http://www.salomon.us.org/ salomon speedcross 4
http://www.airmax95.co.uk/ nike air max 97
http://www.longchampbag.us.com/ longchamp bag
http://www.curry-5shoes.us/ curry
http://www.fila-shoes.us/ fila sneakers
http://www.vapormaxs.us.com/ nike air vapormax flyknit
http://www.monclers.ca/ moncler sale
http://www.louboutinredbottoms.us.com/ christian louboutin
http://www.balenciagas.ca/ balenciaga
http://www.birkenstocksandalssale.us.com/ birkenstock shoes
http://www.jordan11shoes.us.com/ jordan shoes
http://www.katespadepurses.us.com/ kate spade
http://www.adidas-yeezy-shoes.us.com/ Yeezy Boost 350
http://www.nike-airmax270.us.com/ nike air max 90
http://www.christianlouboutins.fr/ christian louboutin
http://www.redbottoms-shoes.us.org/ christian louboutin
http://www.pandora-jewelrysale.us.com/ pandora bracelet
http://www.mizuno-shoes.us/ mizuno
http://www.nikeoffwhite.us.com/ off white clothing
http://www.adidas-ultraboost.us.com/ yeezy boost 350
http://www.pandoracanadacharms.ca/ pandora
http://www.goldengoosesneakerssale.us/ golden goose outlet
http://www.goyards.ca/ goyard tote
http://www.redbottomslouboutinshoes.us.com/ louboutin shoes
http://www.pandora-charmsjewelry.us.com/ pandora jewelry
http://www.katespadebags.us.com/ kate spade
http://www.yeezyshoes.ca/ yeezy shoes
http://www.monclers.us.com/ moncler jacket
http://www.adidasnmdrunnerr1.us.com/ adidas nmd r1
http://www.bijoux-pandora.fr/ pandora
http://www.filas.us.org/ fila sneakers
http://www.bijouxpandoras.fr/ pandora
http://www.ultraboost-uncaged.us/ adidas boost
http://www.skechers.in.net/ skechers sandals
http://www.chaussure-adidas.fr/ adidas chaussure
http://www.monclerjacket.us/ moncler jacket
http://www.salomonspeedcross3.us.com/ salomon speedcross 3
http://www.lebron-16shoes.us/ new lebrons
http://www.birkenstock-sandals.ca/ birkenstock sandals
http://www.charmsstore.us/ pandora charms
http://www.celines.us.com/ celine
http://www.coachbags-outlet.us.com/ coach handbags
http://www.polo-ralphlauren-outlet.us.com/ polo ralph lauren outlet
http://www.airmax90shoes.us.com/ nike vapormax
http://www.goldengoosesale.us/ golden goose sneakers
http://www.pandorajewelryscharms.us.com/ pandora Charms
http://www.nike-vapormax.ca/ nike air max
http://www.airmax270.co.uk/ nike air max 270
http://www.yeezy-750.us/ yeezy boost 350
http://www.chaussure-yeezy.fr/ yeezy boost 350 v2
http://www.nike--shoes.co.uk/ nike outlet
http://www.red-bottoms.us.org/ red bottoms
http://www.giuseppezanottis.us/ giuseppe zanotti sneakers
http://www.nike-airmax.ca/ air max
http://www.philipppleins.us/ philipp plein shoes
http://www.jordan-retro11.us.com/ jordan 11
http://www.ultra-boost.ca/ ultra boost uncaged
http://www.hermesbirkin-handbags.us.com/ Hermes Wallets
http://www.skechers-shoes.ca/ skechers go walk
http://www.nikeairmax270.ca/ air max
http://www.northfacejacketoutlets.us.com/ north face jacket
http://www.balenciagas-sneakers.us.com/ balenciaga
http://www.moncler-uk.co.uk/ moncler jacket mens
http://www.nikelebron15.us.com/ lebron
http://www.nikeairmax-90.us.com/ Nike VaporMax
http://www.air-max.us/ nike
http://www.goyard.org.uk/ goyard london
http://www.adidasyeezy-350.us.com/ yeezy boost 350
http://www.kate-spadepurses.us/ kate spade outlet
http://www.adidas--yeezy.co.uk/ yeezy
http://www.nikeoffwhiteshoes.us/ off white sneakers
http://www.kd11shoes.us/ kevin durant
http://www.red-bottoms.org.uk/ louboutin
http://www.nike-canada.ca/ nike store
http://www.yeezy--shoes.co.uk/ yeezy
http://www.salomonshoes.ca/ salomon shoes
http://www.salvatore-ferragamo.us.com/ ferragamo
http://www.long-champs.us.com/ longchamp handbags
http://www.chaussuresskechers.fr/ skechers
http://www.northface-jacket.us.com/ north face outlet
http://www.nikeairmax-2019.us.com/ air max 2019
http://www.vans--shoes.us.com/ vans shoes
http://www.adidastrainers-uk.co.uk/ adidas trainers
http://www.jordan11.co.uk/ jordan shoes
http://www.fjallravenkankens.us/ fjallraven backpack
http://www.fitflops-sale.us.com/ fitflop
http://www.airmax90.fr/ air max 90
http://www.ferragamoshoess.us.com/ salvatore ferragamo shoes
http://www.doudoune-moncler.fr/ doudoune moncler
http://www.burberry--scarf.us.com/ burberry outlet
http://www.pandoras.in.net/ pandora rings
http://www.adidasyeezyboost.fr/ yeezy boost 350
http://www.yeezys.fr/ yeezy
http://www.kd10-shoes.us.com/ kd shoes
http://www.yeezyboost350shoes.us.com/ yeezy boost 350 v2
http://www.nmd.us.org/ nmd
http://www.eccoshoesoutlets.us.com/ ecco outlet
http://www.louboutin-shoesuk.co.uk/ louboutin shoes
http://www.airmax-2019.us.com/ air max 270
http://www.pandorauk.us.com/ pandora rings
http://www.golden-goosesneakers.us.com/ golden goose sneakers
http://www.nikeairmax97.co.uk/ nike air max
http://www.air-max-270.us.com/ nike air max 270 flyknit
http://www.cartier-bracelet.us.com/ cartier love ring
http://www.katespades.co.uk/ kate spade outlet
http://www.yeezy.in.net/ yeezy boost 350 v2
http://www.fjallravenkanken-backpack.us/ fjallraven kanken
http://www.nikeair-max90.co.uk/ nike air max 90
http://www.monclerjacketwomens.us.com/ moncler jacket
http://www.yeezyboost-350v2.fr/ yeezy
http://www.jordans11shoes.us.com/ jordan 11
http://www.uggsforwomen.us/ uggs for women
http://www.nikeairvapormaxflyknit.us.com/ nike vapormax
http://www.chaussurelouboutinpascher.fr/ louboutin
http://www.giuseppezanottisneakers.us/ giuseppe shoes
http://www.mizunos.us/ mizuno
http://www.james-hardenshoes.us.com/ harden vol 2
http://www.skechers-shoe.us.com/ skechers shoes
http://www.airjordan11spacejam.us.com/ jordan shoes
http://www.redbottom-shoes.co.uk/ louboutin shoes
http://www.adidaschaussure.fr/ chaussure adidas
http://www.ed-hardys.us.com/ ed hardy
http://www.lebron16-shoes.us/ lebron 16
http://www.fitflopsshoes.us.com/ fitflop shoes
http://www.philipppleinoutlet.us/ philipp plein
http://www.jordan-11.fr/ jordan
http://www.jordan--shoes.us.com/ jordan 11
http://www.salomon-chaussures.fr/ salomon speedcross 4
http://www.balenciaga.us.org/ balenciagas
http://www.christianlouboutinredbottoms.us.com/ red bottom shoes
http://www.longchampbackpack.us.com/ longchamp bag
http://www.jordan11.ca/ jordan 11
http://www.pandoras-jewelrys.us.com/ pandora rings
http://www.pandora-bracelet.fr/ bijoux pandora
http://www.bracelet-pandora.fr/ bracelet pandora
http://www.jordan11spacejams.us.com/ jordan space jams
http://www.goyard.in.net/ goyard tote
http://www.adidasyeezyshoes.co.uk/ yeezy
http://www.monclers.uk/ moncler jacket mens
http://www.katespades.ca/ kate spade outlet
http://www.monclerjacket.org.uk/ moncler jacket mens
http://www.pandora--jewelry.us.org/ pandora jewelry
http://www.uggslippers.ca/ ugg canada
http://www.adidaseqt.us.org/ adidas eqt support
http://www.chaussuresalomon.fr/ salomon speedcross 4
http://www.salomonboots.co.uk/ salomon speedcross 4
http://www.nmds.ca/ adidas nmd
http://www.yeezy-500.us/ adidas yeezy 500
http://www.moncler-coat.us.com/ moncler jacket
http://www.nikeairmax.fr/ nike
http://www.nikeairmax270.org.uk/ air max 270
frank님의 댓글
frank 작성일
Yeezy Boost http://www.yeezy-boost.co.uk/
Birkenstock Sandals http://www.birkenstockuk.org.uk/
Supreme Shoes http://www.supremes.us.org/
Coach Purses http://www.coachbagsoutlet.us/
Lebron 15 http://www.lebron-16.us.org/
Curry 6 http://www.curry5shoes.us.org/
Balenciaga Shoes http://www.balenciagasneakers.us/
Yeezy Supply http://www.yeezy-supply.us/
Michael Kors Bags http://www.michaelkorspurse.us/
Fjallraven Kanken http://www.fjallraven.us.com/
Fitflop Sale http://www.fitflopsandals.us/
Nike Air Max 720 http://www.airmax-720.us/
Fjallraven Kanken http://www.fjallravenkanken.us.com/
Vibram 5 Fingers http://www.vibram-fivefingers.us/
Off White Shoes http://www.off-white.us.org/
Jimmy Choo Heels http://www.jimmychooheels.us/
Karen Millen Dresses http://www.karen-millen.us/
Jordan 11 http://www.jordan-11.us/
Air Jordan http://www.jordanshoesoutlet.us/
Giuseppe Zanotti Shoes http://www.giuseppeshoes.us/
Birkenstock http://www.birkenstockcanadasandals.ca/
Off White Shoes http://www.offwhitecanada.ca/
Golden Goose Shoes http://www.goldengoose-shoes.us/
Longchamp Backpack http://www.longchampbackpack.us/
KD 10 http://www.kd-11.us.org/
Ultra Boost Uncaged http://www.adidasultraboost.us.com/
Nike Air Max 95 http://www.airmax-270.co.uk/
Mizuno http://www.mizunoshoes.org/
Skechers Boots http://www.skechersshoes-outlet.us/
hampion Clothing http://www.championhoodie.co.uk/
Louboutin http://www.redbottoms.us.com/
Nike Air Max 720 http://www.nikeairmax720.us/
Supreme Sweatshirt http://www.supremeshirt.us/
Steph Curry http://www.curry5.ca/
Coach Canada http://www.coachbags.ca/
Balenciaga UK http://www.balenciagatrainers.co.uk/
Swarovski Bracelet http://www.swarovskijewelry.us/
Giuseppe Shoes http://www.giuseppeshoes.us.org/
Karen Millen Sale http://www.karen-millen.co.uk/
Skechers Outlet http://www.skechersoutlet.us/
Pandora Charms http://www.pandorajewelrystore.us/
Lauren Ralph Lauren http://www.ralph-laurencanada.ca/
Salomon Shoes http://www.salomon-boots.us/
Vans http://www.vansshoesoutlet.us/
Bape Hoodie http://www.bapeshirt.us/
Birkenstock http://www.birkenstocksandalssale.us/
Champion Sweater http://www.champion-canada.ca/
Jordan Shoes http://www.jordanshoes.ca/
Bvlgari Sunglasses http://www.bvlgaris.us/
Longchamp Outlet http://www.longchamp-canada.ca/
Nike Store http://www.nikecanadashoes.ca/
Supreme http://www.supreme-canada.ca/
Asics Running Shoes http://www.asicscanada.ca/
Adidas Boost http://www.adidasboost.us/
Pandora Jewelry http://www.pandoracanadas.ca/
Birkenstock http://www.birkenstock-canada.ca/
Champion T Shirt http://www.championsweatshirt.us.com/
Bottega Veneta Handbags http://www.bottegavenetas.us/
Fjallraven Backpack http://www.fjallraven-canada.ca/
Christian Louboutin Shoes http://www.christianlouboutin-shoes.us/
Champion Clothing http://www.championhoodie.us.com/
Goyard http://www.goyardcanada.ca/
Adidas Trainers http://www.adidas-trainersuk.org.uk/
Ralph Lauren USA http://www.ralphlaurenusa.us/
Burberry Scarf http://www.burberrybagsuk.co.uk/
Adidas Shoes http://www.adidascanadashoes.ca/
Birkenstock Outlet http://www.birkenstock-sale.us/
Fjallraven Backpack http://www.fjallraven.us.org/
Golden Goose Sneakers http://www.goldengooses.us.org/
Coach Purses http://www.coachbags.co.uk/
Karen Millen http://www.karenmillendresses.co.uk/
Fjallraven http://www.fjallraven.org.uk/
Mont Blanc Pens http://www.mont-blancpens.us/
Vans Old Skool http://www.vanscanada.ca/
Fjallraven Backpack http://www.fjallraven.in.net/
Converse Shoes http://www.converses.us/
Longchamp Backpack http://www.longchampbags-outlet.us/
Cartier http://www.cartier.us.org/
Fitflop Boots http://www.fitflop.org.uk/
Bape Jacket http://www.bapehoodie.co.uk/
Fitflops Clearance http://www.fitflopshoes.us/
Nike Air Max http://www.nikeairmaxoutlet.us/
Yeezy Boost http://www.adidasyeezy.ca/
Golden Goose http://www.goldengoosesneakers.co.uk/
Clarks http://www.clarksshoes.org.uk/
ED Hardy Shirt http://www.edhardyclothing.us/
Ecco http://www.eccoshoessandals.us/
Yeezy Shoes http://www.yeezyboost350v2.us.com/
Bape http://www.bape.org.uk/
Supreme Shirt http://www.supremehoodie.co.uk/
Salomon Speedcross 5 http://www.salomon.in.net/
Harden Shoes http://www.hardenvol3.us/
Converse High Tops http://www.conversecanada.ca/
Vibram Five Fingers http://www.vibram.us.org/
Balenciaga Bags http://www.balenciagashoes.ca/
Suicoke Sale http://www.suicoke.us/
Nike Shox Women http://www.nikeshoxwomen.us/
Burberry Bags http://www.mulberryhandbags.us/
Vans Shoes http://www.vansslipon.us/
Fred Perry Shirt http://www.fredperry.us.org/
Off White Hoodie http://www.offwhites.us/
Kyrie Irving Shoes http://www.kyrie5-shoes.us/
Pandora Canada http://www.pandoracanada.ca/
Pandora Bracelet http://www.pandoraofficialsite.us/
Red Bottoms http://www.redbottomlouboutinshoes.us/
Louboutin Shoes http://www.louboutinredbottoms.us/
Supreme Clothing http://www.supremeclothings.us.com/
Pandora Jewelry http://www.pandoraus.us/
Red Bottom Shoes http://www.louboutinredbottomshoes.us/
KD Shoes http://www.kd11.ca/
MCM Purse http://www.mcmbags.us/
Fila Trainers http://www.filashoes.co.uk/
Giuseppe Zanotti Sale http://www.giuseppezanotti.org.uk/
Coach Purses http://www.coachbags.us/
Polo Ralph Lauren Canada http://www.polo-ralphlauren.ca/
Converse High Tops http://www.converse-uk.co.uk/
Fjallraven Kanken http://www.fjallraven-kanken.us.org/
Michael Kors Handbags http://www.michaelkors-bags.us/
Fila http://www.fila.in.net/
Salvatore Ferragamo Shoes http://www.ferragamo.in.net/
Balenciaga Shoes http://www.balenciagas.us/
Jimmy Choo Outlet http://www.jimmy-chooshoes.us/
Salomon Shoes http://www.salomons.us/
Toms Womens Shoes http://www.toms-shoes.us/
Pandora Rings http://www.pandorarings.us/
Fila Sneakers http://www.filacanada.ca/
Goyard Tote http://www.goyard-bags.us/
Lebron 16 Shoes http://www.lebron16.ca/
Pandora Rings http://www.pandoracanadarings.ca/
Balenciagas http://www.balenciaga-sneakers.us.org/
Asics Shoes http://www.asicsrunningshoes.us/
Lauren Ralph Lauren http://www.ralphlauren-polo.us/
Hydro Flask Sale http://www.hydro-flask.us/
Calvin Klein Bikini http://www.calvinklein.org.uk/
Red Bottom Shoes http://www.christianlouboutinredbottoms.us/
North Face Jacket http://www.northfacejacket.us.org/
Air Max 95 http://www.airmax2019.us/
Pandora Charms http://www.pandora.in.net/
Bape Shark Hoodie http://www.bapecanada.ca/
Nike Outlet http://www.nikeairmaxca.ca/
Louboutin Shoes http://www.louboutintrainers.co.uk/
Nike Air More Uptempo http://www.nikeuptempo.us/
Adidas http://www.adidas-outlet.ca/
Salvatore Ferragamo http://www.ferragamocanada.ca/
Kyrie 5 http://www.kyrie5shoes.us/
Kate Spade Bags http://www.katespadebags.ca/
Hydro Flask 32 OZ http://www.hydroflask.us.org/
Bape Shark Hoodie http://www.bape-hoodie.us/
Birkenstock Shoes http://www.birkenstockoutlet.us/
Puma Shoes http://www.pumacanada.ca/
Kate Spade Wallet http://www.katespade-purses.us.com/
Jordan Shoes http://www.jordan11.org.uk/
Red Bottoms http://www.redbottomsshoes.us/
Air Max 2019 http://www.airmax-2019.us/
Asics Gel http://www.asicsoutlet.us/
New Balance Shoes http://www.newbalanceshoes.us/
Coach Bags http://www.coach-bags.us/
Yezzys http://www.yeezytrainers.co.uk/
Pandora Charms http://www.pandoras.us/
Nike Air Max 270 http://www.nikeairmax-uk.co.uk/
Kate Spade Outlet http://www.katespadecanada.ca/
Vans Shoes http://www.vansoldskool.org.uk/
Birkenstock Shoes http://www.birkenstock-sandals.co.uk/
Yeezy 750 http://www.adidasnmdwomens.us/
Golden Goose Sneakers Sale http://www.goldengoosesneakers.ca/
ernestine님의 댓글
ernestine 작성일
White Air Max 95 Mens http://www.nike-trainersuk.co.uk/white-air-max-95-mens_5598.html
Adidas Ad http://www.yeezy-adidas.us/adidas-ad_7907.html
Adidas Ultraboost Uncaged Shoes http://www.yeezyadidas-shoes.us/adidas-ultraboost-uncaged-shoes_5136.html
Nike Presto Extreme http://www.nikeairmax2019.us/nike-presto-extreme_2748.html
Adidas Two Piece Womens http://www.yeezy-adidas.us/adidas-two-piece-womens_11747.html
Adidas White Leather Sneakers http://www.yeezy-adidas.us/adidas-white-leather-sneakers_8331.html
Nike Air Max Speed Turf Release Date http://www.nikeairmax2019.us/nike-air-max-speed-turf-release-date_4312.html
Nike Tr8 Mens http://www.nikeairmaxshoes.us/nike-tr8-mens_5477.html
Sean Wotherspoon Air Max 97 http://www.nike-trainersuk.co.uk/sean-wotherspoon-air-max-97_5643.html
Vapormax Size 6 http://www.nike-trainersuk.co.uk/vapormax-size-6_4850.html
Mens Stan Smith Trainers http://www.yeezytrainers.org.uk/nmd_r2_6908.html
Air Max Plus Tn Se http://www.nike-trainersuk.co.uk/air-max-plus-tn-se_5646.html
Black And Red Lebron 15 http://www.nikeairmaxshoes.us/black-and-red-lebron-15_6029.html
Pandora Rings For Her http://www.pandorajewelryrings.us/pandora-rings-for-her_2639.html
Adidas Running Trainers Mens http://www.yeezytrainers.org.uk/adidas-spezial-2018_7535.html
Adidas Zx Flux Black http://www.yeezytrainers.org.uk/adidas-zx-flux-black_3451.html
Adidas Superstar Boost http://www.yeezytrainers.org.uk/adidas-superstar-boost_3932.html
Blazer Nike http://www.nikeairmaxshoes.us/blazer-nike_3868.html
Upcoming Air Max 97 http://www.nikeairmaxshoes.us/upcoming-air-max-97_3987.html
Pandora Silver Hoop Earrings http://www.pandoracharmsjewelry.us/pandora-silver-hoop-earrings_2520.html
Adidas Nmd R1 Pink http://www.yeezy-adidas.us/adidas-nmd-r1-pink_8212.html
Mint Green Nike Trainers http://www.nike-trainersuk.co.uk/mint-green-nike-trainers_3011.html
Nike Free Run Mens http://www.nikeairmaxshoes.us/nike-free-run-mens_4463.html
Lebron James 9 http://www.nikeairmax2019.us/lebron-james-9_4888.html
Pandora Vietnam http://www.pandorajewelryrings.us/pandora-vietnam_2195.html
Adidas Superstar Little Kid http://www.yeezy-adidas.us/adidas-superstar-little-kid_8150.html
Adidas Samba Navy http://www.yeezytrainers.org.uk/adidas-samba-navy_4122.html
Solid White Nikes http://www.nikeairmaxshoes.us/solid-white-nikes_3692.html
Black Nike Air Max Size 6 http://www.nike-trainersuk.co.uk/black-nike-air-max-size-6_3863.html
Cuba Pandora Charm http://www.pandorajewelryrings.us/cuba-pandora-charm_2211.html
Pandora Diamond Necklace http://www.pandorajewelryrings.us/pandora-diamond-necklace_2863.html
Polo Ralph Lauren Sweatshirt http://www.ralphlaurenpolo-shirts.us/polo-ralph-lauren-sweatshirt_2167.html
Michael Kors Crossbody Bag http://www.michaelkorswallet.us/michael-kors-crossbody-bag_2275.html
Off White Tm http://www.offwhiteshoesclothing.us/off-white-tm_3615.html
Junior Nike Air Vapormax http://www.nike-trainersuk.co.uk/junior-nike-air-vapormax_2988.html
Nike Free Metcon http://www.nike-trainersuk.co.uk/nike-free-metcon_7010.html
Boys Jordans http://www.jordanretro11shoes.us/boys-jordans_4396.html
Adidas Cloudfoam Super http://www.yeezyadidas-shoes.us/adidas-cloudfoam-super_5000.html
Red Adidas http://www.yeezytrainers.org.uk/red-adidas_3725.html
Are Adidas True To Size http://www.yeezyadidas-shoes.us/are-adidas-true-to-size_4359.html
Adidas Adipure Toe Shoes http://www.yeezy-adidas.us/adidas-adipure-toe-shoes_9802.html
Nike Free Run Rn 2017 http://www.nikeairmax2019.us/nike-free-run-rn-2017_7222.html
Asics Shoes Sale http://www.asicstrainers.us/asics-shoes-sale_3399.html
Nike Roshe Cortez http://www.nikeairmaxshoes.us/nike-roshe-cortez_3378.html
Adidas Originals Superstar White http://www.yeezytrainers.org.uk/adidas-originals-superstar-white_4552.html
Adidas Black Stripe Shoes http://www.yeezy-adidas.us/adidas-black-stripe-shoes_10944.html
Adidas Size 2 http://www.yeezy-adidas.us/adidas-size-2_11644.html
Nike Air Max Price http://www.nike-trainersuk.co.uk/nike-air-max-price_4715.html
Grey Adidas Gazelle Trainers http://www.yeezytrainers.org.uk/grey-adidas-gazelle-trainers_4971.html
Adidas Racquetball Shoes http://www.yeezy-adidas.us/adidas-racquetball-shoes_11350.html
Asics Discount Code http://www.asicstrainers.us/asics-discount-code_4106.html
Nike Air Max 2016 Grey http://www.nikeairmaxshoes.us/nike-air-max-2016-grey_4155.html
Adidas Youth Size http://www.yeezy-adidas.us/adidas-youth-size_8469.html
Pandora Bracelet Store http://www.pandorajewelryrings.us/pandora-bracelet-store_2855.html
Adidas Samba Og Black http://www.yeezytrainers.org.uk/adidas-codes-2019_6679.html
New Nike Free http://www.nikeairmaxshoes.us/new-nike-free_6716.html
Nike Roshe Black White http://www.nike-trainersuk.co.uk/nike-roshe-black-white_8127.html
Adidas Clamshell http://www.yeezyadidas-shoes.us/adidas-clamshell_4436.html
Nike Air Zoom Rev 2019 http://www.nikeairmaxshoes.us/nike-air-zoom-rev-2019_2393.html
Yeezy Mud Rat 500 http://www.yeezytrainers.org.uk/yeezy-mud-rat-500_2412.html
Charms For Pandora Bracelets Cheap http://www.pandoracharmsjewelry.us/charms-for-pandora-bracelets-cheap_2556.html
Adidas Running Shoes Sports Direct http://www.yeezytrainers.org.uk/nmd_r1-shoes_6206.html
Adidas Superstar Weave http://www.yeezy-adidas.us/adidas-superstar-weave_12301.html
Asics Gel Lyte 1 http://www.asicstrainers.us/asics-gel-lyte-1_4017.html
Gold Nike Air Max 2019 http://www.nike-trainersuk.co.uk/gold-nike-air-max-2019_6212.html
Baby Girl Adidas Shoes http://www.yeezytrainers.org.uk/baby-girl-adidas-shoes_5637.html
Yeezy Release Date 2017 http://www.yeezytrainers.org.uk/yeezy-release-date-2017_2908.html
Jd Adidas Flux http://www.yeezytrainers.org.uk/jd-adidas-flux_4714.html
Nmd R1 Grey http://www.yeezyadidas-shoes.us/nmd-r1-grey_3610.html
Air Force One Shoes High Top http://www.nikeairmaxshoes.us/air-force-one-shoes-high-top_3742.html
Off White Presto Authentic http://www.offwhiteshoesclothing.us/off-white-presto-authentic_3264.html
Adidas Boba Fett http://www.yeezy-adidas.us/adidas-boba-fett_10192.html
Nike Lunarepic Low Flyknit 2 Womens Running Shoe http://www.nike-trainersuk.co.uk/nike-lunarepic-low-flyknit-2-womens-running-shoe_8123.html
Air Zoom Mariah Flyknit Racer http://www.nikeairmaxshoes.us/air-zoom-mariah-flyknit-racer_5495.html
Nike 97 Size 8 http://www.nike-trainersuk.co.uk/nike-97-size-8_3120.html
Nmd Sneakers http://www.yeezyadidas-shoes.us/nmd-sneakers_3722.html
Nike Zoom Pegasus Turbo http://www.nikeairmax2019.us/nike-zoom-pegasus-turbo_5980.html
Vapormax Plus Release Dates 2019 http://www.nike-trainersuk.co.uk/vapormax-plus-release-dates-2019_4614.html
Black And Yellow Adidas Shoes http://www.yeezyadidas-shoes.us/black-and-yellow-adidas-shoes_3213.html
Nike Friends And Family Discount http://www.nikeairmax2019.us/nike-friends-and-family-discount_5152.html
Nike Free Motion Flyknit 2019 http://www.nikeairmax2019.us/nike-free-motion-flyknit-2019_6289.html
Adidas Duramo 7 Mens http://www.yeezy-adidas.us/adidas-duramo-7-mens_11873.html
Pandora Ring Sale 2019 http://www.pandoracharmsjewelry.us/pandora-ring-sale-2019_2853.html
Adidas Y3 Yohji Yamamoto http://www.yeezyadidas-shoes.us/adidas-y3-yohji-yamamoto_4498.html
Adidas Tubular Grade School http://www.yeezyadidas-shoes.us/adidas-tubular-grade-school_3073.html
Junior Nike Air Max 2019 http://www.nikeairmaxshoes.us/junior-nike-air-max-2019_4666.html
Nike Janoski White Leather http://www.nikeairmax2019.us/nike-janoski-white-leather_6122.html
Nike Gym Vintage http://www.nikeairmax2019.us/nike-gym-vintage_6672.html
Asics Store http://www.asicstrainers.us/asics-store_3440.html
Air Max 90 Ez White http://www.nikeairmaxshoes.us/air-max-90-ez-white_4113.html
Nike Shoes For Women 2018 http://www.nikeairmax2019.us/nike-shoes-for-women-2018_4203.html
Grey And Black Uggs http://www.uggbootsonsale.us/grey-and-black-uggs_2453.html
Adidas Slides Adilette Black http://www.yeezytrainers.org.uk/adidas-slides-adilette-black_5285.html
Nike Jumpman http://www.nikeairmaxshoes.us/nike-jumpman_4990.html
Nike Ck Racer http://www.nikeairmax2019.us/nike-ck-racer_6058.html
Lebron 8 V2 http://www.nike-trainersuk.co.uk/lebron-8-v2_8483.html
Nike Air Max Jewell White http://www.nike-trainersuk.co.uk/nike-air-max-jewell-white_9382.html
Nike Girls http://www.nikeairmax2019.us/nike-girls_2914.html
Nike Air Zoom Pegasus 34 Review http://www.nike-trainersuk.co.uk/nike-air-zoom-pegasus-34-review_7938.html
Nike Sb Orange http://www.nikeairmax2019.us/nike-sb-orange_4336.html
Nike Jordan Black And White http://www.nikeairmax2019.us/nike-jordan-black-and-white_4918.html
Adidas Future Pacer http://www.yeezytrainers.org.uk/adidas-city-cup-shoes_6426.html
Black Nike Work Boots http://www.nikeairmax2019.us/black-nike-work-boots_5030.html
Vapormax Kids http://www.nike-trainersuk.co.uk/vapormax-kids_3188.html
Pandora Conestoga Mall http://www.pandoracharmsjewelry.us/pandora-conestoga-mall_2752.html
Adidas Outlet Nyc http://www.yeezyadidas-shoes.us/adidas-outlet-nyc_4774.html
Nike Air Vapormax Plus Tropical Sunset http://www.nikeairmax2019.us/nike-air-vapormax-plus-tropical-sunset_6968.html
Air Force 1 Travis Scott http://www.nike-trainersuk.co.uk/air-force-1-travis-scott_3332.html
Lebron 13 Elite http://www.nikeairmax2019.us/lebron-13-elite_4179.html
Off White Air Force 1 For Sale http://www.nike-trainersuk.co.uk/off-white-air-force-1-for-sale_7063.html
Give Me Pandora http://www.pandoracharmsjewelry.us/give-me-pandora_2453.html
Light Pink Adidas Sneakers http://www.yeezy-adidas.us/light-pink-adidas-sneakers_10129.html
Adidas Womens Workout Shoes http://www.yeezy-adidas.us/adidas-womens-workout-shoes_8687.html
Nike Petite http://www.nike-trainersuk.co.uk/nike-petite_7868.html
Mens Gray Adidas Shoes http://www.yeezyadidas-shoes.us/mens-gray-adidas-shoes_4641.html
Yeezy Frozen Yellow http://www.yeezytrainers.org.uk/yeezy-frozen-yellow_2876.html
Nike Air Max 97 Ultra Grey http://www.nike-trainersuk.co.uk/nike-air-max-97-ultra-grey_9425.html
Nike Charles Barkley http://www.nikeairmaxshoes.us/nike-charles-barkley_4165.html
Jordan 1 Purple http://www.jordanretro11shoes.us/jordan-1-purple_4452.html
Skechers Wide Fit Womens http://www.skechersboots.us/skechers-wide-fit-womens_2467.html
Nike Photosynthesis http://www.nikeairmaxshoes.us/nike-photosynthesis_5056.html
His And Hers Nike Shoes http://www.nike-trainersuk.co.uk/his-and-hers-nike-shoes_8603.html
Air Max 95 Original http://www.nike-trainersuk.co.uk/air-max-95-original_4550.html
Michael Kors Mk Bag http://www.michaelkorswallet.us/michael-kors-mk-bag_2391.html
Yellow Adidas Boots http://www.yeezytrainers.org.uk/adidas-originals-gazelle-og_6633.html
Nike Flyknit Racer Uk http://www.nike-trainersuk.co.uk/nike-flyknit-racer-uk_3428.html
Womens Nike Presto Extreme http://www.nikeairmaxshoes.us/womens-nike-presto-extreme_5426.html
Cheap Birkenstocks For Sale http://www.birkenstocksandalsshoes.us/cheap-birkenstocks-for-sale_2380.html
Off White Converse Shop http://www.offwhiteshoesclothing.us/off-white-converse-shop_3229.html
Adidas Nmd Xr1 Og http://www.yeezyadidas-shoes.us/adidas-nmd-xr1-og_3862.html
Nike Flyknit Racer All Black http://www.nikeairmaxshoes.us/nike-flyknit-racer-all-black_2395.html
Stan Smith 2019 http://www.yeezytrainers.org.uk/adidas-cny-2019_6777.html
Ralph Lauren Sale http://www.ralphlaurenpolo-shirts.us/ralph-lauren-sale_2171.html
Pandora Japan Charm http://www.pandoracharmsjewelry.us/pandora-japan-charm_2464.html
Yeezy V2 Yellow http://www.yeezyadidas-shoes.us/yeezy-v2-yellow_2735.html
Kids Nike Shoes Clearance http://www.nikeairmax2019.us/kids-nike-shoes-clearance_4676.html
Nike Pegasus Trainers http://www.nike-trainersuk.co.uk/nike-pegasus-trainers_6598.html
Nike Vapormax Plus Blue http://www.nike-trainersuk.co.uk/nike-vapormax-plus-blue_9246.html
Nmd Triple White http://www.yeezytrainers.org.uk/adidas-platform-sneakers_7119.html
Adidas Classic Kids http://www.yeezy-adidas.us/adidas-classic-kids_8987.html
2019 Adidas Superstar http://www.yeezytrainers.org.uk/2019-adidas-superstar_4915.html
Adidas Factory http://www.yeezytrainers.org.uk/2019-adidas-releases_7551.html
Adidas Barricade Boost 2019 http://www.yeezy-adidas.us/adidas-barricade-boost-2019_7987.html
Kohls Asics http://www.asicstrainers.us/kohls-asics_3812.html
Kyrie Irving New Shoes http://www.nikeairmaxshoes.us/kyrie-irving-new-shoes_6468.html
Air Max 2019 Clearance http://www.nike-trainersuk.co.uk/air-max-2019-clearance_5886.html
Jordan 1 Homage To Home http://www.jordanretro11shoes.us/jordan-1-homage-to-home_3898.html
Yeezy 50 http://www.yeezyadidas-shoes.us/yeezy-50_6020.html
Asics Green http://www.asicstrainers.us/asics-green_3979.html
Adidas Busenitz Pro http://www.yeezy-adidas.us/adidas-busenitz-pro_8996.html
wilma님의 댓글
wilma 작성일
Golden Goose Superstar http://www.goldengoosesneakers.co.uk/
A Bathing Ape http://www.bapeshirt.us/
Pandora Bracelet http://www.pandoraus.us/
Nike Air Max http://www.airmax-720.us/
Adidas NMD http://www.adidasboost.us/
Supreme Shirt http://www.supremeclothings.us.com/
Asics Running Shoes http://www.asicsoutlet.us/
Salomon Shoes http://www.salomons.us/
Birkenstock Sandals http://www.birkenstockcanadasandals.ca/
Fjallraven Backpack http://www.fjallraven.org.uk/
Fjallraven Canada http://www.fjallraven-canada.ca/
Vans Slip On http://www.vansshoesoutlet.us/
Fitflop Sale http://www.fitflop.org.uk/
Birkenstock Sandals http://www.birkenstockuk.org.uk/
Champion Sweatshirt http://www.championhoodie.us.com/
New Balance 574 http://www.newbalanceshoes.us/
Christian Louboutin UK http://www.louboutintrainers.co.uk/
Bape Sweatshirt http://www.bape.org.uk/
Kate Spade Purses http://www.katespade-purses.us.com/
Air Max 270 http://www.airmax-2019.us/
Vibram 5 Fingers http://www.vibram.us.org/
Off White Shoes http://www.offwhitecanada.ca/
Mulberry Purse http://www.mulberryhandbags.us/
Red Bottoms http://www.redbottomsshoes.us/
Pandora Charms http://www.pandorajewelrystore.us/
Pandora Bracelet http://www.pandoracanada.ca/
Goyard http://www.goyardcanada.ca/
Champion Sweatshirt http://www.champion-canada.ca/
Skechers outlet http://www.skechersshoes-outlet.us/
Louboutin Shoes http://www.louboutinredbottoms.us/
Karen Millen http://www.karenmillendresses.co.uk/
Fjallraven Kanken Backpack http://www.fjallraven.us.org/
Adidas Shoes http://www.adidas-outlet.ca/
Air Max 720 http://www.nikeairmax720.us/
Longchamp http://www.longchampbackpack.us/
Pandora Jewelry http://www.pandoras.us/
Lebron Shoes http://www.lebron-16.us.org/
Mizuno Shoes http://www.mizunoshoes.org/
Balenciaga Shoes http://www.balenciagasneakers.us/
Fjallraven Backpack http://www.fjallraven.in.net/
Salomon Speedcross 5 http://www.salomon.in.net/
Off White Sneakers http://www.offwhites.us/
Pandora Charms http://www.pandoracanadas.ca/
Hydro Flask 40 OZ http://www.hydro-flask.us/
Kevin Durant Shoes http://www.kd-11.us.org/
Steph Curry Shoes http://www.curry5shoes.us.org/
Birkenstock http://www.birkenstock-sandals.co.uk/
Pandora Bracelet http://www.pandoraofficialsite.us/
Fjallraven Bags http://www.fjallraven-kanken.us.org/
Nike Uptempo http://www.nikeuptempo.us/
Longchamp Bags http://www.longchamp-canada.ca/
Nike Kyrie http://www.kyrie5shoes.us/
Balenciaga Shoes http://www.balenciagas.us/
Fila High Tops http://www.filashoes.co.uk/
Burberry Shirt http://www.burberrybagsuk.co.uk/
Jimmy Choo Heels http://www.jimmy-chooshoes.us/
Karen Millen Outlet http://www.karen-millen.us/
Air Max 90 http://www.nikeairmax-uk.co.uk/
Birkenstock Sale http://www.birkenstockoutlet.us/
Vans Shoes http://www.vansoldskool.org.uk/
Nike Outlet http://www.nikecanadashoes.ca/
Nike Kyrie http://www.kyrie5-shoes.us/
Fila Disruptor 2 http://www.filacanada.ca/
Asics Kayano http://www.asicsrunningshoes.us/
Vans http://www.vansslipon.us/
Giuseppe Zanotti http://www.giuseppezanotti.org.uk/
Ferragamo Shoes http://www.ferragamo.in.net/
Ralph Lauren Outlet http://www.ralph-laurencanada.ca/
Yeezy Boost http://www.adidasyeezy.ca/
Nike Lebron http://www.lebron16.ca/
Coach Handbags http://www.coachbags.co.uk/
Pandora http://www.pandorarings.us/
Swarovski http://www.swarovskijewelry.us/
Coach Bags http://www.coachbags.ca/
Golden Goose Shoes http://www.goldengoosesneakers.ca/
Louboutin Shoes http://www.redbottomlouboutinshoes.us/
Red Bottoms http://www.louboutinredbottomshoes.us/
Vibram http://www.vibram-fivefingers.us/
Golden Goose Shoes http://www.goldengoose-shoes.us/
Mont Blanc Pen http://www.mont-blancpens.us/
KD 11 Shoes http://www.kd11.ca/
Birkenstock Shoes http://www.birkenstock-sale.us/
Vans Canada http://www.vanscanada.ca/
Ralph Lauren Polo Shirts http://www.ralphlaurenusa.us/
Balenciaga Shoes http://www.balenciaga-sneakers.us.org/
Supreme Shirt http://www.supremeshirt.us/
Yeezy Trainers http://www.yeezy-boost.co.uk/
Nike Air Max 270 http://www.airmax-270.co.uk/
Giuseppe http://www.giuseppeshoes.us/
Nike Shox Women http://www.nikeshoxwomen.us/
Bvlgari Bracelet http://www.bvlgaris.us/
Pandora http://www.pandoracanadarings.ca/
Birkenstock Shoes http://www.birkenstock-canada.ca/
Fila Sneakers http://www.fila.in.net/
Coach Purses http://www.coachbags.us/
Calvin Klein Underwear http://www.calvinklein.org.uk/
Jordan Retro 11 http://www.jordanshoesoutlet.us/
Balenciagas http://www.balenciagashoes.ca/
Converse All Star http://www.conversecanada.ca/
Clarks Shoes http://www.clarksshoes.org.uk/
New Jordans http://www.jordanshoes.ca/
Coach Outlet http://www.coach-bags.us/
Ecco Shoes For Women http://www.eccoshoessandals.us/
Adidas http://www.adidas-trainersuk.org.uk/
Bape Hoodie http://www.bapehoodie.co.uk/
Adidas Superstar http://www.adidascanadashoes.ca/
Red Bottoms http://www.christianlouboutin-shoes.us/
Kate Spade Bags http://www.katespadecanada.ca/
Polo Ralph Lauren Canada http://www.polo-ralphlauren.ca/
Hydro Flask Stickers http://www.hydroflask.us.org/
Nike Air Max http://www.nikeairmaxca.ca/
Golden Goose Sneakers http://www.goldengooses.us.org/
Champion Sweatshirt http://www.championsweatshirt.us.com/
ED Hardy http://www.edhardyclothing.us/
Yeezy Trainers http://www.yeezytrainers.co.uk/
Michael Kors Handbags http://www.michaelkorspurse.us/
Supreme Shirt http://www.supreme-canada.ca/
Yeezy 350 http://www.yeezyboost350v2.us.com/
Ferragamo Belt http://www.ferragamocanada.ca/
Puma http://www.pumacanada.ca/
Salomon Boots http://www.salomon-boots.us/
Bottega http://www.bottegavenetas.us/
Harden Vol 3 http://www.hardenvol3.us/
Goyard Wallet http://www.goyard-bags.us/
Adidas NMD http://www.adidasnmdwomens.us/
Bape Shirt http://www.bape-hoodie.us/
Fred Perry Shoes http://www.fredperry.us.org/
Ultra Boost Uncaged http://www.adidasultraboost.us.com/
Toms Boots http://www.toms-shoes.us/
MCM Bags http://www.mcmbags.us/
Asics Running Shoes http://www.asicscanada.ca/
Fitflop http://www.fitflopsandals.us/
Skechers Sneakers http://www.skechersoutlet.us/
Red Bottom Shoes http://www.redbottoms.us.com/
Ralph Lauren Polo Shirts http://www.ralphlauren-polo.us/
Curry Shoes http://www.curry5.ca/
Christian Louboutin Shoes http://www.christianlouboutinredbottoms.us/
Cartier http://www.cartier.us.org/
Pandora Jewelry http://www.pandora.in.net/
Air Max 95 http://www.airmax2019.us/
Karen Millen http://www.karen-millen.co.uk/
Longchamp Outlet http://www.longchampbags-outlet.us/
Supreme Shirt http://www.supremehoodie.co.uk/
Supreme Sweatshirt http://www.supremes.us.org/
Birkenstock Shoes http://www.birkenstocksandalssale.us/
Kate Spade Purses http://www.katespadebags.ca/
North Face Vest http://www.northfacejacket.us.org/
Fjallraven Kanken http://www.fjallravenkanken.us.com/
Balenciaga Bags http://www.balenciagatrainers.co.uk/
Coach Bags http://www.coachbagsoutlet.us/
Jimmy Choo Heels http://www.jimmychooheels.us/
Giuseppe http://www.giuseppeshoes.us.org/
Off White Shirt http://www.off-white.us.org/
Jordan Retro 11 http://www.jordan-11.us/
Suicoke Moto http://www.suicoke.us/
Converse http://www.converse-uk.co.uk/
Converse Shoes http://www.converses.us/
Nike Shoes http://www.nikeairmaxoutlet.us/
Jordan Shoes http://www.jordan11.org.uk/
Fitflop Sandals http://www.fitflopshoes.us/
Michael Kors Bags http://www.michaelkors-bags.us/
Adidas Yeezy http://www.yeezy-supply.us/
Champion Sweatshirt http://www.championhoodie.co.uk/
Bape Canada http://www.bapecanada.ca/
Fjallraven http://www.fjallraven.us.com/
ernestine님의 댓글
ernestine 작성일
Michael Kors Designer Bags http://www.michaelkorswallet.us/michael-kors-designer-bags_2587.html
Nike Air Max 1 Premium http://www.nike-trainersuk.co.uk/nike-air-max-1-premium_3641.html
Nike Air Max Tavas Uk http://www.nike-trainersuk.co.uk/nike-air-max-tavas-uk_5676.html
Nike Lunarepic Low Flyknit 2 Womens Running Shoe http://www.nike-trainersuk.co.uk/nike-lunarepic-low-flyknit-2-womens-running-shoe_8123.html
Adidas 11 Pro http://www.yeezyadidas-shoes.us/adidas-11-pro_2989.html
Smith Adidas http://www.yeezy-adidas.us/smith-adidas_8316.html
Tiger Vapormax http://www.nike-trainersuk.co.uk/tiger-vapormax_6329.html
Grey And Green Nike Shoes http://www.nikeairmax2019.us/grey-and-green-nike-shoes_5572.html
Adidas Boat Shoes http://www.yeezy-adidas.us/adidas-boat-shoes_9577.html
Red And White Jordans 11 http://www.jordanretro11shoes.us/red-and-white-jordans-11_3781.html
Adidas Gazelle Og White http://www.yeezytrainers.org.uk/boys-adidas-sandals_7472.html
Nike Downshifter http://www.nike-trainersuk.co.uk/nike-downshifter_4131.html
Adidas Campus 80S http://www.yeezyadidas-shoes.us/adidas-campus-80s_4968.html
Size Off White http://www.offwhiteshoesclothing.us/size-off-white_3163.html
Adidas Net Shoes http://www.yeezytrainers.org.uk/adidas-la-trainer-2_6483.html
Pink And Black Lebrons http://www.nike-trainersuk.co.uk/pink-and-black-lebrons_9027.html
Nike Vapormax Boots http://www.nikeairmax2019.us/nike-vapormax-boots_3860.html
Nike Shoes Max http://www.nikeairmaxshoes.us/nike-shoes-max_5374.html
Cq2019 Adidas http://www.yeezytrainers.org.uk/adidas-originals-camo_7287.html
Nike Steel Toe Shoes http://www.nikeairmax2019.us/nike-steel-toe-shoes_2397.html
Nyjah Free Nike Sb http://www.nikeairmaxshoes.us/nyjah-free-nike-sb_6221.html
Skechers White Sandals http://www.skechersboots.us/skechers-white-sandals_2481.html
Nike Zoom Pegasus Boys http://www.nike-trainersuk.co.uk/nike-zoom-pegasus-boys_9239.html
Nike Air Max 2019 Loyal Blue http://www.nikeairmaxshoes.us/nike-air-max-2019-loyal-blue_2258.html
Nike Air 2018 http://www.nikeairmax2019.us/nike-air-2018_4402.html
Adidas Casual Sneakers http://www.yeezy-adidas.us/adidas-casual-sneakers_10099.html
Psny Air Force 1 http://www.nikeairmaxshoes.us/psny-air-force-1_3504.html
Air Force 1 Mid White http://www.nikeairmax2019.us/air-force-1-mid-white_2876.html
Nike Yeezy 2 http://www.nike-trainersuk.co.uk/nike-yeezy-2_7786.html
Footaction Ultra Boost http://www.yeezyadidas-shoes.us/footaction-ultra-boost_5451.html
Asics Gel Equation Womens http://www.asicstrainers.us/asics-gel-equation-womens_4189.html
Ultra Boost Glow In The Dark http://www.yeezyadidas-shoes.us/ultra-boost-glow-in-the-dark_5288.html
Nike Free Trainer 2019 http://www.nike-trainersuk.co.uk/nike-free-trainer-2019_8685.html
Kyrie Irving Shoes All White http://www.nikeairmax2019.us/kyrie-irving-shoes-all-white_6038.html
Nike Mens Air Zoom Pegasus 34 Running Shoes http://www.nikeairmax2019.us/nike-mens-air-zoom-pegasus-34-running-shoes_3247.html
Adidas White Gazelle Trainers http://www.yeezytrainers.org.uk/adidas-white-gazelle-trainers_4447.html
Ugg Clog Boots http://www.uggbootsonsale.us/ugg-clog-boots_2606.html
Boys Red Nike Sneakers http://www.nike-trainersuk.co.uk/boys-red-nike-sneakers_8182.html
Off White Hk Store http://www.offwhiteshoesclothing.us/off-white-hk-store_3087.html
Pandora Halo Ring http://www.pandorajewelryrings.us/pandora-halo-ring_2212.html
Adidas Ultra Boost X Parley http://www.yeezyadidas-shoes.us/adidas-ultra-boost-x-parley_5492.html
Adidas Racer Lite http://www.yeezytrainers.org.uk/adidas-racer-lite_5824.html
Ugg Classic Cardy http://www.uggbootsonsale.us/ugg-classic-cardy_2276.html
Womens Nike Air Max Motion Lw http://www.nikeairmax2019.us/womens-nike-air-max-motion-lw_5811.html
Adidas Bermuda Sale http://www.yeezytrainers.org.uk/adidas-bermuda-sale_4608.html
Adidas Village http://www.yeezy-adidas.us/adidas-village_11051.html
Nike Outlet Coupons July 2019 http://www.nikeairmaxshoes.us/nike-outlet-coupons-july-2019_2333.html
Asics Nyc http://www.asicstrainers.us/asics-nyc_3776.html
Olive Green Presto Extreme http://www.nikeairmaxshoes.us/olive-green-presto-extreme_7325.html
Nike Kawa Shower Slide http://www.nikeairmaxshoes.us/nike-kawa-shower-slide_4119.html
Ugg Scuff Slippers http://www.uggbootsonsale.us/ugg-scuff-slippers_2610.html
Nike Air Force 1 Low 2019 http://www.nikeairmax2019.us/nike-air-force-1-low-2019_7170.html
Pandora Valentine Charms http://www.pandoracharmsjewelry.us/pandora-valentine-charms_3067.html
Red Air Jordans http://www.jordanretro11shoes.us/red-air-jordans_3834.html
Nike Air Max Grey Mens http://www.nike-trainersuk.co.uk/nike-air-max-grey-mens_2773.html
Best Nike Shoes Of 2019 http://www.nikeairmax2019.us/best-nike-shoes-of-2019_5037.html
Nike Vapormax Og http://www.nikeairmaxshoes.us/nike-vapormax-og_6736.html
Nike Laceless http://www.nikeairmaxshoes.us/nike-laceless_4698.html
White Nike Tanjun Womens http://www.nikeairmaxshoes.us/white-nike-tanjun-womens_4170.html
Jordan Future Low http://www.jordanretro11shoes.us/jordan-future-low_4024.html
Nmd Og Black http://www.yeezyadidas-shoes.us/nmd-og-black_3805.html
Nike Lunar Converge http://www.nikeairmax2019.us/nike-lunar-converge_5539.html
Ultra Boost Sneakers http://www.yeezyadidas-shoes.us/ultra-boost-sneakers_5216.html
Pandora Princess http://www.pandorajewelryrings.us/pandora-princess_2794.html
All Black Adidas http://www.yeezytrainers.org.uk/all-black-adidas_3784.html
Supreme Site http://www.supreme-shirt.us/supreme-site_2291.html
Adidas Tubular Big Kids http://www.yeezy-adidas.us/adidas-tubular-big-kids_8935.html
Nike Running Free Run Flyknit 2019 http://www.nikeairmaxshoes.us/nike-running-free-run-flyknit-2019_5673.html
Yeezys In 2019 http://www.yeezytrainers.org.uk/yeezys-in-2019_2298.html
Balenciaga Runners Men http://www.balenciagashoessneakers.us/balenciaga-runners-men_2161.html
Air Max Penny 2 http://www.nikeairmax2019.us/air-max-penny-2_6310.html
Nike Air Max Thea Womens Black http://www.nikeairmaxshoes.us/nike-air-max-thea-womens-black_4065.html
Off White Blazer Mens http://www.offwhiteshoesclothing.us/off-white-blazer-mens_3390.html
Nike Tns Khaki Green http://www.nike-trainersuk.co.uk/nike-tns-khaki-green_5788.html
Nike Flex 2019 Rn Red http://www.nikeairmax2019.us/nike-flex-2019-rn-red_2952.html
Off White Fashion http://www.offwhiteshoesclothing.us/off-white-fashion_3137.html
Nike Sb Junior http://www.nike-trainersuk.co.uk/nike-sb-junior_6657.html
Supreme Stuff For Sale http://www.supreme-shirt.us/supreme-stuff-for-sale_2332.html
Birkenstock Price In Germany http://www.birkenstocksandalsshoes.us/birkenstock-price-in-germany_2419.html
Baby Girl Adidas http://www.yeezytrainers.org.uk/human-race-nmd-march-2019_7618.html
Yeezy Boost 350 V2 Cream White http://www.yeezytrainers.org.uk/yeezy-boost-350-v2-cream-white_2170.html
Pandora 5 http://www.pandorajewelryrings.us/pandora-5_2708.html
Adidas Swift Run Ladies http://www.yeezytrainers.org.uk/adidas-swift-run-ladies_4668.html
Nike Shoes Latest Model 2019 http://www.nikeairmax2019.us/nike-shoes-latest-model-2019_3536.html
Asics Gel Resolution 6 Mens http://www.asicstrainers.us/asics-gel-resolution-6-mens_4132.html
Adidas Climacool Running Shoes http://www.yeezyadidas-shoes.us/adidas-climacool-running-shoes_3062.html
Pandora Charm 2019 http://www.pandoracharmsjewelry.us/pandora-charm-2019_2327.html
Womens Air Max 270 http://www.nike-trainersuk.co.uk/womens-air-max-270_4942.html
Nike Womens Flex Rn 2019 http://www.nikeairmax2019.us/nike-womens-flex-rn-2019_3740.html
Nike Air Force 1 Off White http://www.nike-trainersuk.co.uk/nike-air-force-1-off-white_2806.html
Adidas Forum Low Shoes http://www.yeezy-adidas.us/adidas-forum-low-shoes_11400.html
White Air Force 1 High http://www.nikeairmaxshoes.us/white-air-force-1-high_3981.html
Adidas Originals Flux http://www.yeezytrainers.org.uk/adidas-originals-flux_5010.html
Mens Lebrons http://www.nikeairmax2019.us/mens-lebrons_4617.html
Pandora Wedding Ring Sets http://www.pandorajewelryrings.us/pandora-wedding-ring-sets_2538.html
Nike Air Max 97 Taupe http://www.nike-trainersuk.co.uk/nike-air-max-97-taupe_6485.html
Yeezy 350 Copper http://www.yeezyadidas-shoes.us/yeezy-350-copper_2249.html
Air Max 97 Laces http://www.nike-trainersuk.co.uk/air-max-97-laces_4880.html
Supreme Store New York http://www.supreme-shirt.us/supreme-store-new-york_2207.html
All White Adidas Basketball Shoes http://www.yeezyadidas-shoes.us/all-white-adidas-basketball-shoes_3163.html
Adidas Latest Shoes 2019 http://www.yeezy-adidas.us/adidas-latest-shoes-2019_9519.html
New Vapormax 2019 http://www.nikeairmaxshoes.us/new-vapormax-2019_6889.html
Adidas Climacool 1 Black http://www.yeezytrainers.org.uk/adidas-junction-one_7230.html
White Vapormax Womens http://www.nikeairmax2019.us/white-vapormax-womens_5741.html
Nike Roshe Two Men http://www.nikeairmaxshoes.us/nike-roshe-two-men_5778.html
Adidas Five Finger Shoes http://www.yeezytrainers.org.uk/adidas-five-finger-shoes_4962.html
Nike Hyperdunk 2019 Draymond Green http://www.nikeairmax2019.us/nike-hyperdunk-2019-draymond-green_5031.html
Adidas Adios Boost 2 http://www.yeezy-adidas.us/adidas-adios-boost-2_10493.html
Pandora Bracelet Review http://www.pandoracharmsjewelry.us/pandora-bracelet-review_2744.html
Nike Mayfly Woven Mens http://www.nike-trainersuk.co.uk/nike-mayfly-woven-mens_2902.html
Nike Trainers Size 10 http://www.nike-trainersuk.co.uk/nike-trainers-size-10_4470.html
Nike Roshe Red And Black http://www.nike-trainersuk.co.uk/nike-roshe-red-and-black_8884.html
Adidas Pool Slides http://www.yeezy-adidas.us/adidas-pool-slides_9782.html
Kanye West New Baby http://www.yeezyadidas-shoes.us/kanye-west-new-baby_2801.html
Adidas Ball http://www.yeezytrainers.org.uk/infant-boys-adidas-trainers_6871.html
Adidas Nmd Og http://www.yeezy-adidas.us/adidas-nmd-og_8905.html
Nike Air Jordan I Men http://www.nikeairmax2019.us/nike-air-jordan-i-men_4417.html
Footasylum Vapormax http://www.nike-trainersuk.co.uk/footasylum-vapormax_2547.html
Mens Air Max 1 http://www.nike-trainersuk.co.uk/mens-air-max-1_5026.html
Nike Air Zoom Mariah Flyknit Racer White http://www.nike-trainersuk.co.uk/nike-air-zoom-mariah-flyknit-racer-white_7976.html
Adidas Yeezy Website http://www.yeezy-adidas.us/adidas-yeezy-website_10968.html
Jordan Future Men http://www.jordanretro11shoes.us/jordan-future-men_4306.html
Pandora Pharmacy http://www.pandoracharmsjewelry.us/pandora-pharmacy_2785.html
Adidas Off White Nmd http://www.yeezyadidas-shoes.us/adidas-off-white-nmd_3845.html
Adidas Ultra Boost Colorways 2019 http://www.yeezytrainers.org.uk/adidas-ultra-boost-colorways-2019_3101.html
Adidas Khaki Swift Run Trainers http://www.yeezytrainers.org.uk/adidas-khaki-swift-run-trainers_3993.html
Nike Presto Extreme Blue http://www.nikeairmaxshoes.us/nike-presto-extreme-blue_4140.html
Nike Sf Air Force http://www.nikeairmax2019.us/nike-sf-air-force_6744.html
Ultra Boost Rainbow http://www.yeezyadidas-shoes.us/ultra-boost-rainbow_5348.html
Nike Air Jordan Retro Girls http://www.nikeairmaxshoes.us/nike-air-jordan-retro-girls_4225.html
Vapormax Black And Orange http://www.nikeairmax2019.us/vapormax-black-and-orange_4736.html
Nike Metcon http://www.nike-trainersuk.co.uk/nike-metcon_8544.html
Asics Ronnie Fieg http://www.asicstrainers.us/asics-ronnie-fieg_4125.html
Adidas Gazelle Custom http://www.yeezytrainers.org.uk/adidas-gazelle-custom_5599.html
Air Max Shoes http://www.nikeairmax2019.us/air-max-shoes_2380.html
Asics Nimbus 19 Mens http://www.asicstrainers.us/asics-nimbus-19-mens_4212.html
Skechers Website http://www.skechersboots.us/skechers-website_2218.html
2019 Nike Air Max Red http://www.nikeairmaxshoes.us/2019-nike-air-max-red_3116.html
Adidas Zx Flux Xeno Reflective http://www.yeezy-adidas.us/adidas-zx-flux-xeno-reflective_11802.html
Cheap Nike Huarache http://www.nikeairmaxshoes.us/cheap-nike-huarache_5982.html
Nike Lebron Xv http://www.nike-trainersuk.co.uk/nike-lebron-xv_7261.html
Baby Girl Jordans http://www.jordanretro11shoes.us/baby-girl-jordans_4395.html
Kanye West 2003 http://www.yeezyadidas-shoes.us/kanye-west-2003_5508.html
Nike Promo September 2019 http://www.nikeairmax2019.us/nike-promo-september-2019_5890.html
How To Add Variety To Pandora http://www.pandoracharmsjewelry.us/how-to-add-variety-to-pandora_2733.html
Adidas Originals Iniki http://www.yeezytrainers.org.uk/y3-store_6720.html
White Adidas Deerupt http://www.yeezytrainers.org.uk/white-adidas-deerupt_5212.html
Nike Air Max Classic Mens http://www.nike-trainersuk.co.uk/nike-air-max-classic-mens_6401.html
Adidas Nmd Womens Grey http://www.yeezy-adidas.us/adidas-nmd-womens-grey_8651.html
Skechers Bungee Sneakers http://www.skechersboots.us/skechers-bungee-sneakers_2420.html
magaret님의 댓글
magaret 작성일
http://www.jordanretro11.us/ Jordan Retro 11 Low
http://www.uggbootsforwomen.us/ Ugg Slippers
http://www.goldengoosesneakers.org.uk/ Golden Goose Superstar
http://www.bottegavenetabags.us/ Bottega Veneta Handbags
http://www.moncler-jacket.org.uk/ Moncler Outlet
http://www.ralphlaurencom.us/ Ralph Lauren
http://www.supreme-clothing.ca/ Supreme Clothing
http://www.northfacecanada.ca/ North Face Outlet
http://www.uggsonsale.us/ Ugg
http://www.offwhiteshoes.ca/ Off White T Shirt
http://www.yeezy-static.us/ Yeezy Shoes
http://www.balenciagasneakers.org/ Balenciagas
http://www.skecherssneakers.us/ Skechers Sneakers
http://www.hydro-flask.co.uk/ Hydro Flask Lids
http://www.hydroflask.in.net/ Hydro Flask Sale
http://www.skechers-shoes.co.uk/ Skechers Sandals
http://www.yeezycanada.ca/ Yeezy Canada
http://www.longchamp.in.net/ Longchamp Tote
http://www.northfacejacket.co.uk/ North Face Backpack
http://www.hydroflask.org.uk/ Hydro Flask UK
http://www.skecherscanadashoes.ca/ Skechers Boots
http://www.valentinoshoessale.us/ Valentino
http://www.goyards.co.uk/ Goyard Tote
http://www.northface-canada.ca/ North Face Vest
http://www.airmax95.us.com/ Air Max 90
http://www.ugg-canada.ca/ Ugg
http://www.mizunorunningshoes.us.org/ Mizuno Shoes
http://www.birkenstock-uk.co.uk/ Birkenstock Shoes
http://www.pandorajewelry.ca/ Pandora
http://www.filashoesoutlet.us/ Fila Shoes
http://www.coachcanadabags.ca/ Coach
http://www.supremeclothingshirt.us.com/ Supreme
http://www.ugg-bootsuk.org.uk/ Ugg Slippers
http://www.saucony.in.net/ Saucony Running Shoes
http://www.sauconyrunningshoes.us/ Saucony Womens Shoes
http://www.timberland-uk.co.uk/ Timberland Boots
http://www.skechersgowalk.org.uk/ Skechers Go Walk
http://www.supreme-hoodie.us/ Supreme
http://www.championhoodie.us/ Champion
http://www.jordanretroshoes.us/ Jordan Shoes
http://www.vansoldskool.us.com/ Vans Old Skool
http://www.pandoraringscanada.ca/ Pandora
http://www.hydro-flask.us.com/ Hydro Flask 40 OZ
http://www.yslbags.us/ Yves Saint Laurent
http://www.michaelkors.us.org/ Michael Kors Outlet
http://www.timberlandboots.ca/ Timberland Canada
http://www.goldengoosesneakers-sale.us/ Golden Goose Sneakers
http://www.brooks.us.org/ Brooks Shoes
http://www.asicsshoesoutlet.us/ Asics Shoes
http://www.ralphlauren-shirts.us/ Polo Ralph Lauren
http://www.offwhiteclothing.us/ Off White Clothing
http://www.uggslippers.co.uk/ Ugg
http://www.fjallravenkanken.org.uk/ Fjallraven UK
http://www.underarmour.org.uk/ Under Armour
http://www.nikeuk.co.uk/ Air Max 97
http://www.pandorajewelryonline.us/ Pandora Charms
http://www.goldengoosecanada.ca/ Golden Goose Sneakers
http://www.burberryhandbagsoutlet.us/ Burberry Scarf
http://www.balenciagashoes.co.uk/ Balenciaga Bags
http://www.off-white.org.uk/ Off White Hoodie
http://www.northfaces.us/ North Face Coats
http://www.fjallravens.us.org/ Fjallraven Kanken
http://www.nikeuk-trainers.co.uk/ Nike Shoes
http://www.underarmour-canada.ca/ Under Armour Canada
http://www.birkenstocksale.us/ Birkenstock Sandals
http://www.katespadebags.us/ Kate Spade Handbags
http://www.calvinkleindresses.us/ Calvin Klein Dresses
http://www.giuseppe.us.org/ Giuseppe
http://www.yezzys.co.uk/ Yezzys
http://www.thenorth-face.us/ North Face
http://www.ultra-boost.co.uk/ Adidas Trainers
http://www.hydroflasksale.us/ Hydro Flask 40 OZ
http://www.pandorauk-jewelry.co.uk/ Pandora Earrings
http://www.yeezy-v3.us/ Adidas Yeezy
http://www.monclerjacketoutlet.us/ Moncler Sale
http://www.birkenstocksandals-uk.co.uk/ Birkenstock UK
http://www.valentinoshoes.ca/ Valentino Sneakers
http://www.fitflopsclearance.us/ Fitflops Clearance
http://www.monclercanada.ca/ Moncler Canada
http://www.fjallravens.ca/ Fjallraven Kanken
http://www.timberlandboots-outlet.us/ Timberland
http://www.fjallraven-kanken.co.uk/ Fjallraven Sale
http://www.karen-millen.org.uk/ Karen Millen
http://www.mcmhandbags.us/ MCM Wallet
http://www.montblanc.org.uk/ Mont Blanc Refills
http://www.pradacanada.ca/ Prada Bags
http://www.hydroflaskcanada.ca/ Hydro Flask Water Bottle
http://www.northfacejacket.us/ North Face Jacket
http://www.nikeshoesca.ca/ Nike Shoes
http://www.birkenstockcanada-sandals.ca/ Birkenstock Shoes
http://www.brooksshoes.us/ Brooks Shoes
http://www.valentinosneakers.us/ Valentino Shoes
http://www.offwhitehoodie.us/ Off White Clothing
http://www.airmax-270.org.uk/ Nike Air Max
http://www.monclerjacketsoutlet.us/ Moncler
sandra님의 댓글
sandra 작성일
http://www.yezzys.co.uk/ Yezzys
http://www.offwhitehoodie.us/ Off White
http://www.skechers-shoes.co.uk/ Skechers UK
http://www.goldengoosesneakers.org.uk/ Golden Goose
http://www.monclercanada.ca/ Moncler Canada
http://www.birkenstockcanada-sandals.ca/ Birkenstock Shoes
http://www.birkenstocksandals-uk.co.uk/ Birkenstock
http://www.ralphlaurencom.us/ Ralph Lauren
http://www.championhoodie.us/ Champion
http://www.yeezy-static.us/ Yeezy Static
http://www.pandoraringscanada.ca/ Pandora
http://www.hydro-flask.co.uk/ Hydro Flask Lids
http://www.goldengoosecanada.ca/ Golden Goose
http://www.yslbags.us/ YSL Purse
http://www.hydroflasksale.us/ Hydro Flask Stickers
http://www.hydroflask.in.net/ Hydro Flask Stickers
http://www.montblanc.org.uk/ Mont Blanc Fountain Pen
http://www.moncler-jacket.org.uk/ Moncler Outlet
http://www.offwhiteshoes.ca/ Off White Hoodie
http://www.calvinkleindresses.us/ Calvin Klein Outlet
http://www.underarmour.org.uk/ Under Armour Shoes
http://www.ultra-boost.co.uk/ Adidas Ultra Boost UK
http://www.mcmhandbags.us/ MCM Bags
http://www.birkenstock-uk.co.uk/ Birkenstock Shoes
http://www.pradacanada.ca/ Prada Handbags
http://www.katespadebags.us/ Kate Spade Purses
http://www.jordanretroshoes.us/ Jordan Retro
http://www.northfacecanada.ca/ North Face Outlet
http://www.longchamp.in.net/ Longchamp Purse
http://www.yeezycanada.ca/ Yeezy Supply
http://www.valentinoshoessale.us/ Valentino Shoes
http://www.sauconyrunningshoes.us/ Saucony Sneakers
http://www.balenciagashoes.co.uk/ Balenciaga Bags
http://www.asicsshoesoutlet.us/ Asics Shoes
http://www.uggbootsforwomen.us/ Ugg Boots
http://www.uggslippers.co.uk/ Ugg
http://www.supreme-clothing.ca/ Supreme
http://www.fjallraven-kanken.co.uk/ Fjallraven Kanken
http://www.nikeuk-trainers.co.uk/ Nike Shoes
http://www.giuseppe.us.org/ Giuseppe Zanotti Sale
http://www.hydroflaskcanada.ca/ Hydro Water Bottle
http://www.nikeuk.co.uk/ Nike UK
http://www.coachcanadabags.ca/ Coach Outlet Canada
http://www.supreme-hoodie.us/ Supreme
http://www.airmax95.us.com/ Air Max 95
http://www.thenorth-face.us/ North Face
http://www.skecherscanadashoes.ca/ Skechers
http://www.mizunorunningshoes.us.org/ Mizuno Sneakers
http://www.northfaces.us/ The North Face
http://www.michaelkors.us.org/ Michael Kors Bags
http://www.hydroflask.org.uk/ Hydro Flask Sale
http://www.hydro-flask.us.com/ Hydro Flask Sale
http://www.pandorajewelryonline.us/ Pandora Charms
http://www.timberlandboots-outlet.us/ Timberland Boots
http://www.filashoesoutlet.us/ Fila Clothing
http://www.skecherssneakers.us/ Skechers Sneakers
http://www.supremeclothingshirt.us.com/ Supreme Jacket
http://www.monclerjacketsoutlet.us/ Moncler Sale
http://www.valentinoshoes.ca/ Valentino Canada
http://www.brooks.us.org/ Brooks Running Shoes
http://www.ugg-canada.ca/ Ugg Canada
http://www.monclerjacketoutlet.us/ Moncler Sale
http://www.goyards.co.uk/ Goyard Bags
http://www.saucony.in.net/ Saucony Sneakers
http://www.offwhiteclothing.us/ Off White Hoodie
http://www.fjallravens.us.org/ Fjallraven Kanken Backpack
http://www.underarmour-canada.ca/ Under Armour Outlet
http://www.northfacejacket.co.uk/ North Face UK
http://www.skechersgowalk.org.uk/ Skechers Sandals
http://www.karen-millen.org.uk/ Karen Millen Dresses
http://www.airmax-270.org.uk/ Nike Air Max 97
http://www.burberryhandbagsoutlet.us/ Burberry Wallet
http://www.northface-canada.ca/ North Face Vest
http://www.northfacejacket.us/ North Face Backpack
http://www.jordanretro11.us/ Jordan 11
http://www.nikeshoesca.ca/ Nike Canada
http://www.fjallravenkanken.org.uk/ Fjallraven UK
http://www.bottegavenetabags.us/ Bottega Veneta
http://www.timberland-uk.co.uk/ Timberland
http://www.off-white.org.uk/ Off White T Shirt
http://www.ugg-bootsuk.org.uk/ Ugg
http://www.yeezy-v3.us/ Yeezy Shoes
http://www.uggsonsale.us/ Uggs For Men
http://www.brooksshoes.us/ Brooks Shoes
http://www.fitflopsclearance.us/ Fitflop Shoes
http://www.timberlandboots.ca/ Timberland Boots
http://www.fjallravens.ca/ Fjallraven Canada
http://www.ralphlauren-shirts.us/ Polo Shirts
http://www.vansoldskool.us.com/ Vans Sneakers
http://www.pandorajewelry.ca/ Pandora Charms
http://www.pandorauk-jewelry.co.uk/ Pandora Rings
http://www.goldengoosesneakers-sale.us/ Golden Goose Shoes
http://www.balenciagasneakers.org/ Balenciaga Bags
http://www.birkenstocksale.us/ Birkenstock Outlet
http://www.valentinosneakers.us/ Valentino Shoes Sale
leigh님의 댓글
leigh 작성일
http://www.balenciagasneakers.org/ Balenciaga Shoes
http://www.off-white.us.org/ Off White Clothing
http://www.nikeuk.co.uk/ Air Max 97
http://www.pandoraofficialsite.us/ Pandora Jewelry
http://www.calvinkleindresses.us/ Calvin Klein Underwear
http://www.fjallraven.us.com/ Fjallraven Bags
http://www.off-white.org.uk/ Off White
http://www.ferragamo.in.net/ Salvatore Ferragamo
http://www.hydroflask.in.net/ Hydro Flask Stickers
http://www.birkenstockoutlet.us/ Birkenstock Sale
http://www.converse-uk.co.uk/ Converse Trainers
http://www.hydroflask.org.uk/ Hydro Flask
http://www.adidascanadashoes.ca/ Adidas Shoes
http://www.uggslippers.co.uk/ Ugg Slippers
http://www.ralphlaurencom.us/ Ralph Lauren Dresses
http://www.underarmour-canada.ca/ Under Armour
http://www.giuseppezanotti.org.uk/ Zanotti
http://www.birkenstocksale.us/ Birkenstock Outlet
http://www.salomon-boots.us/ Salomon Gtx
http://www.brooks.us.org/ Brooks Shoes
http://www.brooksshoes.us/ Brooks
http://www.hydroflask.us.org/ Hydro Flask Sale
http://www.nikeshoxwomen.us/ Nike Shox
http://www.hardenvol3.us/ Harden Vol 3
http://www.airmax-270.org.uk/ Nike Air Max 90
http://www.kyrie5-shoes.us/ Kyrie 4
http://www.nikeairmaxca.ca/ Nike Shoes
http://www.championsweatshirt.us.com/ Champion Hoodie
http://www.championhoodie.co.uk/ Champion Clothing
http://www.goldengoosesneakers.org.uk/ Golden Goose Sneakers
http://www.lebron-16.us.org/ Lebron 16 Shoes
http://www.calvinklein.org.uk/ Calvin Klein Underwear
http://www.birkenstockuk.org.uk/ Birkenstock
http://www.vansshoesoutlet.us/ Vans Old Skool
http://www.longchamp.in.net/ Longchamp Tote
http://www.katespade-purses.us.com/ Kate Spade
http://www.mcmhandbags.us/ MCM Bags
http://www.northfacejacket.co.uk/ North Face Jacket
http://www.vibram-fivefingers.us/ Vibram
http://www.polo-ralphlauren.ca/ Ralph Lauren Outlet
http://www.burberrybagsuk.co.uk/ Burberry Bags
http://www.louboutinredbottoms.us/ Christian Louboutin
http://www.coachbags.ca/ Coach
http://www.yeezy-boost.co.uk/ Yeezy
http://www.pandoraus.us/ Pandora Bracelet
http://www.yeezycanada.ca/ Yeezy Canada
http://www.ugg-bootsuk.org.uk/ Ugg
http://www.michaelkors.us.org/ Michael Kors Wallet
http://www.birkenstockcanadasandals.ca/ Birkenstock Sandals
http://www.nikeuptempo.us/ Nike Air Uptempo
http://www.fjallravens.us.org/ Fjallraven Bags
http://www.curry5.ca/ Curry 5
http://www.balenciaga-sneakers.us.org/ Balenciaga Sneakers
http://www.lebron16.ca/ Lebron 15
http://www.valentinoshoessale.us/ Valentino Sneakers
http://www.filashoes.co.uk/ Fila
http://www.northfacejacket.us/ North Face Outlet
http://www.mizunoshoes.org/ Mizuno
http://www.yeezyboost350v2.us.com/ Yeezy 350
http://www.goyardcanada.ca/ Goyard Wallet
http://www.fjallraven.in.net/ Fjallraven Bags
http://www.offwhites.us/ Off White Hoodie
http://www.pandorajewelryonline.us/ Pandora Charms
http://www.fila.in.net/ Fila
http://www.skecherscanadashoes.ca/ Skechers Outlet
http://www.fredperry.us.org/ Fred Perry
http://www.birkenstocksandalssale.us/ Birkenstock
http://www.redbottomsshoes.us/ Christian Louboutin Heels
http://www.yeezytrainers.co.uk/ Yezzys
http://www.northfacejacket.us.org/ North Face Outlet
http://www.hydro-flask.us.com/ Hydro Flask Sale
http://www.adidas-outlet.ca/ Adidas Shoes For Men
http://www.bottegavenetabags.us/ Bottega Veneta Bags
http://www.yslbags.us/ YSL Purse
http://www.montblanc.org.uk/ Mont Blanc Fountain Pen
http://www.katespadebags.us/ Kate Spade Handbags
http://www.yezzys.co.uk/ Yeezy Shoes
http://www.underarmour.org.uk/ Under Armour
http://www.saucony.in.net/ Saucony Sneakers
http://www.goldengoosesneakers.ca/ Golden Goose Shoes
http://www.karen-millen.org.uk/ Karen Millen Dresses
http://www.redbottoms.us.com/ Louboutin
http://www.nikeairmaxoutlet.us/ Nike Air Max 270
http://www.nikecanadashoes.ca/ Nike Store
http://www.kd-11.us.org/ KD 11 shoes
http://www.salomons.us/ Salomon Boots
http://www.longchampbackpack.us/ Longchamp Handbags
http://www.fjallraven.org.uk/ Fjallraven Backpack
http://www.fjallravenkanken.us.com/ Fjallraven Kanken
http://www.asicsrunningshoes.us/ Asics Shoes
http://www.fitflopsclearance.us/ Fitflop Outlet
http://www.converses.us/ Converse Sneakers
http://www.pandora.in.net/ Pandora
http://www.karen-millen.co.uk/ Karen Millen Sale
http://www.balenciagasneakers.us/ Balenciagas
http://www.curry5shoes.us.org/ Curry 5 Shoes
http://www.balenciagatrainers.co.uk/ Balenciaga Runners
http://www.louboutintrainers.co.uk/ Louboutin Trainers
http://www.giuseppeshoes.us.org/ Giuseppe Zanotti Heels
http://www.valentinoshoes.ca/ Valentino
http://www.nikeairmax720.us/ Aike Air Max
http://www.jordan-11.us/ New Jordans
http://www.bapehoodie.co.uk/ Bape Clothing
http://www.goldengooses.us.org/ Golden Goose Sneakers Sale
http://www.fjallraven-kanken.co.uk/ Fjallraven Sale
http://www.redbottomlouboutinshoes.us/ Christian Louboutin Shoes
http://www.goldengoosesneakers.co.uk/ Golden Goose
http://www.hydro-flask.co.uk/ Hydro Flask Sale
http://www.mulberryhandbags.us/ Mulberry Handbags
http://www.fjallraven-kanken.us.org/ Fjallraven Kanken
http://www.offwhitecanada.ca/ Off White Canada
http://www.mizunorunningshoes.us.org/ Mizuno Running Shoes
http://www.birkenstocksandals-uk.co.uk/ Birkenstock UK
http://www.championhoodie.us.com/ Champion
http://www.balenciagashoes.co.uk/ Balenciaga Shoes
http://www.birkenstock-uk.co.uk/ Birkenstock
http://www.moncler-jacket.org.uk/ Moncler Coat
http://www.airmax95.us.com/ Nike Shoes
http://www.ralphlauren-polo.us/ Ralph Lauren Polo Shirts
http://www.fjallraven.us.org/ Fjallraven
http://www.suicoke.us/ Suicoke Shoes
http://www.bape.org.uk/ Bape Clothing
http://www.coachbagsoutlet.us/ Coach Bags
http://www.timberlandboots.ca/ Timberland Canada
http://www.adidasultraboost.us.com/ Ultra Boost
http://www.airmax-2019.us/ Air Max 270
http://www.vansoldskool.us.com/ Vans Old Skool
http://www.yeezy-v3.us/ Yeezy Shoes
http://www.goyards.co.uk/ Goyard
http://www.coachcanadabags.ca/ Coach Bags
http://www.ultra-boost.co.uk/ Ultra Boost
http://www.ralph-laurencanada.ca/ Polo Ralph Lauren
http://www.toms-shoes.us/ Toms Womens Shoes
http://www.karenmillendresses.co.uk/ Karen Millen Sale
http://www.vibram.us.org/ Vibram Five Fingers
http://www.goldengoosesneakers-sale.us/ Golden Goose
http://www.jordan11.org.uk/ Jordan 12
http://www.coach-bags.us/ Coach Purses
http://www.supremeclothingshirt.us.com/ Supreme Shirt
http://www.jordanshoesoutlet.us/ Air Jordan
http://www.adidasnmdwomens.us/ Adidas NMD Womens
http://www.fjallravenkanken.org.uk/ Fjallraven Bags
http://www.fitflopshoes.us/ Fitflop Sandals
http://www.pandorauk-jewelry.co.uk/ Pandora
http://www.giuseppe.us.org/ Giuseppe Zanotti Shoes
http://www.supreme-canada.ca/ Supreme
http://www.asicscanada.ca/ Asics Running Shoes
http://www.pandorarings.us/ Pandora
http://www.salomon.in.net/ Salomon
http://www.vansoldskool.org.uk/ Vans Shoes
http://www.fitflopsandals.us/ Fitflop Sandals
http://www.goldengoose-shoes.us/ Golden Goose Superstar Sneakers
http://www.skechersshoes-outlet.us/ Skechers outlet
http://www.valentinosneakers.us/ Valentino Shoes
dominick님의 댓글
dominick 작성일
http://www.airmax270sale.us/ Air Max 720
http://www.karenmillendresses.org.uk/ Karen Millen Outlet
http://www.goyardbags.org.uk/ Goyard
http://www.asicstrainers.co.uk/ Asics Shoes
http://www.calvin-klein.org.uk/ Calvin Klein Jeans
http://www.northfacejackets.org.uk/ North Face Outlet
http://www.champion-sweatshirt.us/ Champion Clothing
http://www.clark-shoes.us/ Clarks Sandals
http://www.cartier-lovebracelet.us/ Cartier Bracelet
http://www.fitflop-sandals.us/ Fitflop Sandals
http://www.canadgoosejacket.us/ Canada Goose Coat
http://www.hugobosssuits.us/ Hugo Boss
http://www.adidas-yeezy.ca/ Adidas Yeezy
http://www.merrellboots.us/ Merrell Outlet
http://www.bapehoodie.ca/ Bape Shirt
http://www.burberry-scarf.co.uk/ Burberry UK
http://www.northfaceoutlet.co.uk/ North Face Jacket
http://www.jordan-11.org.uk/ Jordan 11
http://www.birkenstocksale.org.uk/ Birkenstock Shoes
http://www.lacosteoutlet.us/ Lacoste Shirts
http://www.monclerjacketwomens.us/ Moncler T Shirt
http://www.bvlgari-jewelry.us/ Bvlgari
http://www.michaelkorshandbagsoutlet.us/ Michael Kors Purse
http://www.longchampbackpackbags.us/ Longchamp Tote
http://www.louboutintrainers.org.uk/ Louboutin
http://www.adidasstasmith.us/ Stan Smith
http://www.birkenstocksandals-sale.us/ Birkenstock
http://www.bosestore.us/ Bose
http://www.balenciagashoes.org.uk/ Balenciaga
http://www.filashoes.org.uk/ Fila Dress
http://www.canadagoose-jacket.ca/ Canada Goose Coat
http://www.katespadebags.org.uk/ Kate Spade Outlet
http://www.lululemonpants.ca/ Lululemon Pants
http://www.fjallravenkankenofficialsite.us/ Fjallraven Kanken Official Site
http://www.mcmbackpackbags.us/ MCM Purse
http://www.merrell-shoes.us/ Merrell Hiking Shoes
http://www.bose.org.uk/ Bose Bluetooth Speaker
http://www.jackwolfskin.org.uk/ Jack Wolfskin Parka
http://www.air-max90.us/ Air Max 90
http://www.northfacejacketsoutlet.us/ North Face Outlet
http://www.nikeuk-trainers.org.uk/ Nike Air Force
http://www.karenmillenoutlet.us/ Karen Millen Coats
http://www.brooks-shoes.us/ Brooks Running Shoes
http://www.jackwolfskinjackets.org.uk/ Jack Wolfskin Coat
http://www.championhoodie.ca/ Champion Clothing
http://www.katespade-bags.ca/ Kate Spade Outlet
http://www.boseheadphonesstore.us/ Bose Earphones
http://www.karenmillendresses.us/ Karen Millen
http://www.goyard-bags.co.uk/ Goyard
http://www.balenciagas.org.uk/ Balenciaga Bags
http://www.filaclothing.us/ Fila Clothing
http://www.longchamp.org.uk/ Longchamp Tote
http://www.monclersale.us/ Moncler Jacket
http://www.boseheadphones.co.uk/ Bose Speakers
http://www.coachbags.org.uk/ Coach Purses
http://www.filashoesshirt.us/ Fila
http://www.fjallraven-kanken.org.uk/ Fjallraven Backpack
http://www.christianlouboutinheels.us/ Red Bottoms
http://www.katespadebags.co.uk/ Kate Spade Purses
http://www.fitflopshoes.co.uk/ Fitflop UK
http://www.birkenstocksale.co.uk/ Birkenstock
http://www.birkenstocksandals.ca/ Birkenstock Canada
http://www.monclercoat.co.uk/ Moncler Sale
http://www.adidas-zxflux.us/ Adidas Gazelle
http://www.juicycouturetracksuit.us/ Juicy Couture Tracksuit
http://www.ecco-shoes.ca/ Ecco Shoes Canada
http://www.montblancpens.org.uk/ Mont Blanc
http://www.birkenstocksandals-outlet.us/ Birkenstock Sandals
http://www.giuseppe.org.uk/ Giuseppe Zanotti Trainers
http://www.nikecanadaoutlet.ca/ Nike Canada
http://www.goldengoosetrainers.co.uk/ Golden Goose Sneakers Sale
http://www.asicscanadashoes.ca/ Asics Shoes
http://www.airmax2020.us/ Air Max 270
http://www.fendishoes.us/ Fendi
http://www.championsweatshirt.us/ Champion Clothing
http://www.bapeclothing.co.uk/ Bape Hoodie
http://www.clarks-canada.ca/ Clarks Shoes
http://www.fjallraven-backpack.us/ Fjallraven Kanken Backpack
http://www.lululemonleggingsoutlet.us/ Lululemon Yoga Mat
http://www.fjallravenkanken.ca/ Fjallraven Kanken
http://www.north-facejacket.us/ North Face Outlet
http://www.lebron-17.us/ Lebron James Shoes
http://www.jordan-11.us.com/ Jordan 13
http://www.champion-hoodie.us/ Champion Sweatshirt
http://www.jordan-33.us/ Jordan 11
http://www.michaelkors-purse.us/ Michael Kors Purse
http://www.airmax90.co.uk/ Nike UK
http://www.lacoste-shoes.us/ Lacoste Polo Shirts
http://www.fila-canada.ca/ Fila Shoes
http://www.karenmillenuk.org.uk/ Karen Millen UK
http://www.hydroflaskwaterbottle.us/ Hydro Flask 32 OZ
http://www.mont-blanc.org.uk/ Mont Blanc Pens
http://www.bapehoodie.org.uk/ Bape Shirt
http://www.air-max720.us/ Air Max 270
http://www.adidasyeezy.us/ Yeezy 500
http://www.asicswomensshoes.us/ Asics
http://www.goyardbagsstore.us/ Goyard
http://www.converseallstar.us/ Converse Shoes
http://www.hydroflask-sale.us/ Hydro Flask Sale
http://www.eccosandals.us/ Ecco Sandals
http://www.asicsrunningshoes.co.uk/ Asics
http://www.canadagoosejacketsoutlet.us/ Canada Goose Jacket
http://www.juicycoutureoutlet.us/ Juicy Couture Tracksuit
http://www.boseheadphones.ca/ Bose Canada
http://www.airmax270.ca/ Air Max 720
http://www.katespadenewyork.us/ Kate Spade
http://www.converse-canada.ca/ Converse
http://www.mizunousa.us/ Mizuno
http://www.clarks-outlet.co.uk/ Clarks UK
http://www.balenciaga-shoes.ca/ Balenciaga Shoes
http://www.columbiajackets.us/ Columbia Fleece Jacket
http://www.adidasshoes.org.uk/ Adidas Shoes
http://www.curry6-shoes.us/ Curry 6 Shoes
http://www.conversetrainers.co.uk/ Converse High Tops
http://www.calvinklein-dresses.us/ Calvin Klein Shoes
http://www.ferragamos.us/ Ferragamo Sandals
http://www.championsweatshirt.co.uk/ Champion Sweatshirt
http://www.ferragamoshoes.ca/ Salvatore Ferragamo
http://www.fjallravenbackpack.co.uk/ Fjallraven Backpack
http://www.championtshirt.us/ Champion Sweatshirt
http://www.hydroflaskuk.co.uk/ Hydro Flask Sale
http://www.fitflopshoessandals.us/ Fitflop Boots
http://www.adidas-yeezy.co.uk/ Yeezy
http://www.converseshoes-outlet.us/ Converse Outlet
http://www.burberrybags.org.uk/ Burberry Bags
http://www.katespade-canada.ca/ Kate Spade Outlet
http://www.bose-wirelessheadphones.us/ Bose Headphones
http://www.coachbags-outlet.us/ Coach Wallet
http://www.giuseppe-shoes.us/ Giuseppe
http://www.goldengoose.org.uk/ Golden Goose Trainers
http://www.eccoshoes-outlet.us/ Ecco Boots
http://www.northfacebackpack.us/ North Face Jacket
http://www.goldengoose-sale.us/ Golden Goose Sale
http://www.bose-canada.ca/ Bose Headphones
http://www.coachpurses.us/ Coach Backpack
http://www.canadagoosejacketuk.co.uk/ Canada Goose Sale
http://www.addidasnmd.us/ Adidas Shoes
http://www.cartiercanada.ca/ Cartier Ring
http://www.adidascanadaoutlet.ca/ Yeezy Canada
http://www.championhoodie.org.uk/ Champion Clothing
http://www.bottegaveneta-handbags.us/ Bottega Veneta
http://www.goldengoosesneakerssale.co.uk/ Golden Goose Sneakers Sale
http://www.hugobossjeans.us/ Hugo Boss
http://www.montblancpensoutlet.us/ Mont Blanc Outlet
http://www.hydroflasks.ca/ Hydro Flask Lids
http://www.nike-shoes.org.uk/ Nike Air Max
http://www.jordan-shoes.ca/ New Jordans
http://www.laurenralphlauren.us/ Ralph Lauren
http://www.columbiaclothing.us/ Columbia Clothing
http://www.bapeshirt.us.com/ Bape Sweater
http://www.hydro-flask.org.uk/ Hydro Flask Lids
http://www.fendibags.us/ Fendi Boots
http://www.calvinkleinunderwear.org.uk/ Calvin Klien
http://www.calvinkleincanada.ca/ Calvin Klein Underwear
http://www.lululemons.us/ Lululemon Sale
sandra님의 댓글
sandra 작성일
http://www.lululemons.us/ Lululemon Yoga Mat
http://www.hydro-flask.org.uk/ Hydro Flask UK
http://www.filaclothing.us/ Fila Clothing
http://www.fitflop-sandals.us/ Fitflop Slippers
http://www.canadagoose-jacket.ca/ Canada Goose Outlet
http://www.airmax270sale.us/ Air Max 90
http://www.fitflopshoessandals.us/ Fitflop Outlet
http://www.goyardbags.org.uk/ Goyard Handbags
http://www.converseshoes-outlet.us/ Converse Slip On
http://www.juicycouturetracksuit.us/ Juicy Couture Handbags
http://www.asicsrunningshoes.co.uk/ Asics Shoes
http://www.nikecanadaoutlet.ca/ Air Max 97
http://www.coachbags-outlet.us/ Coach Purses
http://www.fendibags.us/ Fendi Boots
http://www.bose-canada.ca/ Bose Speakers
http://www.fjallravenbackpack.co.uk/ Fjallraven Backpack
http://www.adidasyeezy.us/ Yeezy
http://www.burberry-scarf.co.uk/ Burberry Bags
http://www.air-max90.us/ Air Max 720
http://www.laurenralphlauren.us/ Ralph Lauren
http://www.bapeclothing.co.uk/ Bape
http://www.bapehoodie.ca/ Bape Clothing
http://www.katespade-canada.ca/ Kate Spade Wallet
http://www.monclersale.us/ Moncler Jacket
http://www.championsweatshirt.us/ Champion Hoodie
http://www.lacoste-shoes.us/ Lacoste
http://www.goyard-bags.co.uk/ Goyard Bags
http://www.merrell-shoes.us/ Merrell Boots
http://www.montblancpens.org.uk/ Mont Blanc Pen
http://www.championhoodie.ca/ Champion Hoodie
http://www.curry6-shoes.us/ Curry
http://www.bottegaveneta-handbags.us/ Bottega Veneta Wallet
http://www.jackwolfskin.org.uk/ Jack Wolfskin Coat
http://www.monclercoat.co.uk/ Moncler Outlet
http://www.northfacejackets.org.uk/ The North Face
http://www.canadagoosejacketsoutlet.us/ Canada Goose Parka
http://www.birkenstocksandals-outlet.us/ Birkenstock Shoes
http://www.northfacejacketsoutlet.us/ The North Face
http://www.balenciagashoes.org.uk/ Balenciaga Bags
http://www.adidasstasmith.us/ Stan Smith
http://www.eccosandals.us/ Ecco Sandals
http://www.longchamp.org.uk/ Longchamp Purse
http://www.filashoesshirt.us/ Fila
http://www.katespadenewyork.us/ Kate Spade Purses
http://www.columbiaclothing.us/ Columbia Jacket
http://www.lebron-17.us/ Nike Lebron 17
http://www.mcmbackpackbags.us/ MCM Wallet
http://www.christianlouboutinheels.us/ Christian Louboutin Heels
http://www.columbiajackets.us/ Columbia Fleece Jacket
http://www.coachbags.org.uk/ Coach To London
http://www.giuseppe.org.uk/ Giuseppe
http://www.fjallravenkankenofficialsite.us/ Fjallraven
http://www.montblancpensoutlet.us/ Mont Blanc Ballpoint Pen
http://www.burberrybags.org.uk/ Burberry Bags
http://www.bose-wirelessheadphones.us/ Bose
http://www.conversetrainers.co.uk/ Converse Trainers
http://www.jackwolfskinjackets.org.uk/ Jack Wolfskin Parka
http://www.hydroflask-sale.us/ Hydro Flask 32 OZ
http://www.giuseppe-shoes.us/ Guiseppes
http://www.merrellboots.us/ Merrell Outlet
http://www.fjallraven-backpack.us/ Fjallraven Sale
http://www.ferragamoshoes.ca/ Ferragamo
http://www.canadagoosejacketuk.co.uk/ Canada Goose Sale
http://www.airmax90.co.uk/ Nike UK
http://www.balenciagas.org.uk/ Balenciagas
http://www.asicswomensshoes.us/ Asics
http://www.clark-shoes.us/ Clarks
http://www.goldengoosetrainers.co.uk/ Golden Goose Superstar
http://www.boseheadphones.co.uk/ Bose Soundlink Mini
http://www.filashoes.org.uk/ Fila Sweatshirt
http://www.bosestore.us/ Bose Headphones
http://www.calvinkleincanada.ca/ Calvin Klein Dresses
http://www.air-max720.us/ Air Max 270
http://www.calvinkleinunderwear.org.uk/ Calvin Klein Underwear
http://www.clarks-outlet.co.uk/ Clarks
http://www.goldengoose-sale.us/ Golden Goose Sneakers
http://www.jordan-11.org.uk/ Nike Jordan
http://www.fjallraven-kanken.org.uk/ Fjallraven Kanken Backpack
http://www.airmax2020.us/ Air Max
http://www.ferragamos.us/ Ferragamo Sandals
http://www.addidasnmd.us/ Yeezy Boost 350
http://www.fjallravenkanken.ca/ Fjallraven Backpack
http://www.katespadebags.org.uk/ Kate Spade UK
http://www.goldengoose.org.uk/ Golden Goose Sneakers
http://www.eccoshoes-outlet.us/ Ecco Boots
http://www.adidasshoes.org.uk/ Adidas Shoes
http://www.hugobossjeans.us/ Hugo Boss Shoes
http://www.fila-canada.ca/ Fila Shoes
http://www.boseheadphonesstore.us/ Bose Wireless Headphones
http://www.champion-sweatshirt.us/ Champion Shoes
http://www.jordan-33.us/ Jordan Shoes
http://www.hydroflasks.ca/ Hydro Flask Lids
http://www.asicstrainers.co.uk/ Asics Trainers
http://www.bose.org.uk/ Bose Soundlink Mini
http://www.balenciaga-shoes.ca/ Balenciaga Shoes
http://www.northfaceoutlet.co.uk/ North Face Outlet
http://www.lululemonleggingsoutlet.us/ Lululemon
http://www.mizunousa.us/ Mizuno Wave Rider
http://www.airmax270.ca/ Nike Air Max 270
http://www.ecco-shoes.ca/ Ecco
http://www.katespadebags.co.uk/ Kate Spade Wallet
http://www.michaelkors-purse.us/ Michael Kors Bags
http://www.karenmillenoutlet.us/ Karen Millen Coats
http://www.fendishoes.us/ Fendi
http://www.lacosteoutlet.us/ Lacoste Jacket
http://www.goyardbagsstore.us/ Goyard Tote
http://www.bvlgari-jewelry.us/ Bvlgari Earrings
http://www.fitflopshoes.co.uk/ Fit Flops
http://www.goldengoosesneakerssale.co.uk/ Golden Goose Superstar
http://www.karenmillendresses.org.uk/ Karen Millen Tops
http://www.katespade-bags.ca/ Kate Spade Purses
http://www.championtshirt.us/ Champion Shoes
http://www.adidas-yeezy.co.uk/ Yeezy Boost 350
http://www.karenmillendresses.us/ Karen Millen Coats
http://www.bapeshirt.us.com/ Bape
http://www.converse-canada.ca/ Converse
http://www.calvinklein-dresses.us/ Calvin Klein Jeans
http://www.louboutintrainers.org.uk/ Louboutin Trainers
http://www.birkenstocksandals.ca/ Birkenstock Sale
http://www.adidas-zxflux.us/ Adidas ZX Flux
http://www.bapehoodie.org.uk/ Bape Hoodie
http://www.adidascanadaoutlet.ca/ Adidas Canada
http://www.converseallstar.us/ Converse Outlet
http://www.clarks-canada.ca/ Clarks Boots
http://www.mont-blanc.org.uk/ ont Blanc Pen
http://www.longchampbackpackbags.us/ Longchamp Purse
http://www.championhoodie.org.uk/ Champion Sweater
http://www.championsweatshirt.co.uk/ Champion Sweatshirt
http://www.birkenstocksale.org.uk/ Birkenstock Shoes
http://www.lululemonpants.ca/ Lululemon Yoga Mat
http://www.hydroflaskwaterbottle.us/ Hydro Flask Stickers
http://www.jordan-11.us.com/ Jordan Shoes
http://www.north-facejacket.us/ North Face Backpack
http://www.cartier-lovebracelet.us/ Cartier Jewelry
http://www.asicscanadashoes.ca/ Asics
http://www.birkenstocksale.co.uk/ Birkenstock UK
http://www.michaelkorshandbagsoutlet.us/ Michael Kors Purse
http://www.karenmillenuk.org.uk/ Karen Millen Sale
http://www.hydroflaskuk.co.uk/ Hydro Flask 32 OZ
http://www.nike-shoes.org.uk/ Nike UK
http://www.champion-hoodie.us/ Champion Shoes
http://www.cartiercanada.ca/ Cartier
http://www.monclerjacketwomens.us/ Moncler T Shirt
http://www.juicycoutureoutlet.us/ Juicy Couture Sweatsuit
http://www.coachpurses.us/ Coach Bags
http://www.brooks-shoes.us/ Brooks
http://www.northfacebackpack.us/ North Face Outlet
http://www.canadgoosejacket.us/ Canada Goose Outlet
http://www.calvin-klein.org.uk/ Calvin Klien
http://www.boseheadphones.ca/ Bose Speakers
http://www.nikeuk-trainers.org.uk/ Air Max 97
http://www.hugobosssuits.us/ Hugo Boss
http://www.birkenstocksandals-sale.us/ Birkenstock
http://www.jordan-shoes.ca/ Jordan 11
http://www.adidas-yeezy.ca/ Adidas Canada
ronald님의 댓글
ronald 작성일
http://www.salomons.us/ Salomon Speedcross 4
http://www.redbottomlouboutinshoes.us/ Christian Louboutin Shoes
http://www.vansoldskool.org.uk/ Vans Trainers
http://www.louboutintrainers.co.uk/ Christian Louboutin
http://www.coachbags.ca/ Coach Purses
http://www.vibram-fivefingers.us/ Vibram Five Fingers
http://www.championhoodie.co.uk/ Champion Sweatshirt
http://www.championsweatshirt.us.com/ Champion Sweatshirt
http://www.giuseppezanotti.org.uk/ Giuseppe Zanotti Trainers
http://www.curry5.ca/ Curry 6
http://www.hydroflask.us.org/ Hydro Flask
http://www.timberlandboots.ca/ Timberland Boots
http://www.michaelkors.us.org/ Michael Kors Purse
http://www.ralph-laurencanada.ca/ Polo Ralph Lauren
http://www.hydroflask.org.uk/ Hydro Flask UK
http://www.fjallraven.us.com/ Fjallraven
http://www.pandoraofficialsite.us/ Pandora Jewelry
http://www.valentinoshoessale.us/ Valentino Sneakers
http://www.nikeairmax720.us/ Nike Air Max 720
http://www.adidas-outlet.ca/ Adidas Shoes
http://www.jordan-11.us/ Jordan Retro
http://www.fjallraven.org.uk/ Fjallraven Kanken Sale
http://www.nikeshoxwomen.us/ Nike Outlet
http://www.ugg-bootsuk.org.uk/ Ugg Slippers
http://www.longchamp.in.net/ Longchamp Bags
http://www.goldengoosesneakers-sale.us/ Golden Goose Sale
http://www.vibram.us.org/ Vibram 5 Fingers
http://www.goyards.co.uk/ Goyard Bags
http://www.longchampbackpack.us/ Longchamp
http://www.saucony.in.net/ Saucony Womens Shoes
http://www.suicoke.us/ Suicoke Sale
http://www.hydroflask.in.net/ Hydro Flask Stickers
http://www.airmax95.us.com/ Air Max 95
http://www.airmax-2019.us/ Nike Air Max
http://www.vansshoesoutlet.us/ High Top Vans
http://www.goldengoose-shoes.us/ Golden Goose Sneakers
http://www.mcmhandbags.us/ MCM
http://www.supremeclothingshirt.us.com/ Supreme
http://www.underarmour.org.uk/ Under Armour Trainers
http://www.yeezycanada.ca/ Yeezy Canada
http://www.nikeuptempo.us/ Nike Air More Uptempo
http://www.birkenstocksandalssale.us/ Birkenstock Outlet
http://www.birkenstockoutlet.us/ Birkenstock Sale
http://www.converses.us/ Converse Sneakers
http://www.yeezyboost350v2.us.com/ Adidas Yeezy
http://www.giuseppeshoes.us.org/ Giuseppe Shoes
http://www.pandoraus.us/ Pandora
http://www.bapehoodie.co.uk/ A Bathing Ape
http://www.polo-ralphlauren.ca/ Ralph Lauren Canada
http://www.giuseppe.us.org/ Giuseppe Zanotti Sale
http://www.louboutinredbottoms.us/ Louboutin Shoes
http://www.balenciagasneakers.us/ Balenciagas
http://www.birkenstockuk.org.uk/ Birkenstock UK
http://www.calvinklein.org.uk/ Calvin Klein
http://www.airmax-270.org.uk/ Nike Air Max 97
http://www.fjallravenkanken.org.uk/ Fjallraven Backpack
http://www.fitflopshoes.us/ Fitflop
http://www.pandorajewelryonline.us/ Pandora Jewelry
http://www.goldengooses.us.org/ Golden Goose Shoes
http://www.northfacejacket.us.org/ The North Face
http://www.skechersshoes-outlet.us/ Skechers Boots
http://www.coachcanadabags.ca/ Coach Bags
http://www.kd-11.us.org/ KD 11
http://www.asicsrunningshoes.us/ Asics Running Shoes
http://www.fila.in.net/ Fila Shoes Womens
http://www.salomon.in.net/ Salomon Boots
http://www.hydro-flask.co.uk/ Hydro Flask Lids
http://www.birkenstocksale.us/ Birkenstock Shoes
http://www.pandorarings.us/ Pandora Jewelry
http://www.balenciagatrainers.co.uk/ Balenciaga Shoes
http://www.balenciaga-sneakers.us.org/ Balenciaga
http://www.valentinosneakers.us/ Valentino Shoes
http://www.goldengoosesneakers.org.uk/ Golden Goose Superstar
http://www.fjallravens.us.org/ Fjallraven Backpack
http://www.offwhitecanada.ca/ Off White
http://www.montblanc.org.uk/ Mont Blanc
http://www.balenciagasneakers.org/ Balenciaga Bags
http://www.fjallraven.in.net/ Fjallraven Kanken
http://www.fredperry.us.org/ Fred Perry T Shirt
http://www.fitflopsclearance.us/ Fitflop Sale
http://www.ralphlauren-polo.us/ Ralph Lauren Polo Shirts
http://www.asicscanada.ca/ Asics Shoes
http://www.hardenvol3.us/ Harden Vol 2
http://www.uggslippers.co.uk/ Uggs On Sale
http://www.brooksshoes.us/ Brooks Tennis Shoes
http://www.pandora.in.net/ Pandora Jewelry Official Site
http://www.nikeuk.co.uk/ Nike Air Max
http://www.bape.org.uk/ Bape Hoodie
http://www.katespade-purses.us.com/ Kate Spade Handbags
http://www.jordanshoesoutlet.us/ Jordan Retro 11
http://www.yslbags.us/ YSL Purse
http://www.coach-bags.us/ Coach Purses
http://www.underarmour-canada.ca/ Under Armour Shoes
http://www.skecherscanadashoes.ca/ Skechers Shoes
http://www.vansoldskool.us.com/ Vans Shoes
http://www.off-white.us.org/ Off White Shirt
http://www.jordan11.org.uk/ Jordan 11
http://www.goldengoosesneakers.co.uk/ Golden Goose Sneakers
http://www.valentinoshoes.ca/ Valentino Sneakers
http://www.toms-shoes.us/ Toms Womens Shoes
http://www.katespadebags.us/ Kate Spade
http://www.ultra-boost.co.uk/ Adidas Trainers
http://www.adidasnmdwomens.us/ Adidas NMD
http://www.karen-millen.co.uk/ Karen Millen
http://www.karenmillendresses.co.uk/ Karen Millen Outlet
http://www.kyrie5-shoes.us/ Kyrie Irving Shoes
http://www.nikeairmaxca.ca/ Nike CA
http://www.off-white.org.uk/ Off White T Shirt
http://www.fjallraven.us.org/ Fjallraven Backpack
http://www.moncler-jacket.org.uk/ Moncler Outlet
http://www.calvinkleindresses.us/ Calvin Klein Dresses
http://www.curry5shoes.us.org/ Curry 5 Shoes
http://www.salomon-boots.us/ Salomon Boots
http://www.northfacejacket.co.uk/ North Face Outlet
http://www.fjallraven-kanken.co.uk/ Fjallraven UK
http://www.filashoes.co.uk/ Fila Trainers
http://www.birkenstocksandals-uk.co.uk/ Birkenstock Sale
http://www.yeezy-v3.us/ Yeezy
http://www.hydro-flask.us.com/ Hydro Flask Sale
http://www.mulberryhandbags.us/ Mulberry Bayswater
http://www.balenciagashoes.co.uk/ Balenciaga
http://www.mizunorunningshoes.us.org/ Mizuno Sneakers
http://www.championhoodie.us.com/ Champion T Shirt
http://www.northfacejacket.us/ North Face Outlet
http://www.goldengoosesneakers.ca/ Golden Goose Sale
http://www.birkenstock-uk.co.uk/ Birkenstock Sandals
http://www.yeezy-boost.co.uk/ Yeezy Trainers
http://www.birkenstockcanadasandals.ca/ Birkenstock Sandals
http://www.burberrybagsuk.co.uk/ Burberry
http://www.pandorauk-jewelry.co.uk/ Pandora Earrings
http://www.nikeairmaxoutlet.us/ Nike Air Max 270
http://www.coachbagsoutlet.us/ Coach
http://www.lebron-16.us.org/ Lebron 16
http://www.brooks.us.org/ Brooks
http://www.karen-millen.org.uk/ Karen Millen UK
http://www.ralphlaurencom.us/ Ralph Lauren Com
http://www.converse-uk.co.uk/ Converse
http://www.adidasultraboost.us.com/ Adidas Originals Ultra Boost
http://www.lebron16.ca/ Lebron 16 Shoes
http://www.offwhites.us/ Off White Hoodie
http://www.fitflopsandals.us/ Fitflop Shoes
http://www.bottegavenetabags.us/ Bottega Veneta Bags
http://www.mizunoshoes.org/ Mizuno Golf
http://www.fjallravenkanken.us.com/ Fjallraven Bags
http://www.nikecanadashoes.ca/ Nike Air Max
http://www.ferragamo.in.net/ Salvatore Ferragamo Shoes
http://www.adidascanadashoes.ca/ Adidas Outlet
http://www.yezzys.co.uk/ Yeezy
http://www.redbottomsshoes.us/ Christian Louboutin
http://www.goyardcanada.ca/ Goyard Bags
http://www.supreme-canada.ca/ Supreme Canada
http://www.fjallraven-kanken.us.org/ Fjallraven Kanken
http://www.yeezytrainers.co.uk/ Yezzys
http://www.redbottoms.us.com/ Red Bottom Shoes
antonio님의 댓글
antonio 작성일
http://www.off-whiteshoes.us/ Nike Off White
http://www.offwhiteshirt.us/ Off White
http://www.superdryjacket.us/ Superdry Sale
http://www.timberlandbootsstore.us/ Timberland Store
http://www.yezzys.org.uk/ Yeezy Shoes
http://www.stevemaddensneakers.us/ Steve Madden Slip Ons
http://www.uggbootsstore.us/ UGGS For Women
http://www.pradabags.org.uk/ Prada Bags
http://www.riverislanddresses.co.uk/ River Island Clothes
http://www.yeezyboost350.fr/ Adidas Yeezy
http://www.reebok.org.uk/ Reebok
http://www.vibramshoes.us/ Vibram
http://www.salvatoreferragamo.org.uk/ Salvatore Ferragamo Shoes
http://www.pumarihannafenty.us/ Puma Suede
http://www.chaussurenikeofficiel.fr/ Air Max 97
http://www.puma-canada.ca/ Puma Shoes
http://www.scarpehogan.eu/ Scarpe Hogan
http://www.puma-shoes.co.uk/ Puma
http://www.tomsboots.us/ Toms Womens Shoes
http://www.supremeclothing-uk.co.uk/ Supreme Hoodie
http://www.toryburch-outlet.us/ Tory Burch
http://www.riverislandsale.co.uk/ River Island Shoes
http://www.valentinosandals.us/ Valentino Shoes
http://www.superdryhoodie.co.uk/ Superdry UK
http://www.air-max.fr/ Air Max 95
http://www.reebok-classic.us/ Reebok
http://www.pandoraringsuk.co.uk/ Pandora UK
http://www.conversefemme.fr/ Converse Pas Cher
http://www.balenciagaus.us/ Balenciaga Bags
http://www.vans-canada.ca/ Vans Outlet
http://www.ultra-boost.us/ Adidas Shoes
http://www.bapehoodieoutlet.us/ Bape Outlet
http://www.yeezys.eu/ Adidas Scarpe
http://www.supremeclothingcanada.ca/ Supreme Clothing
http://www.supremeclothingshop.us/ Supreme Coats
http://www.vansshoes.org.uk/ Vans
http://www.pumaschuhedamen.de/ Puma Hoodie
http://www.doudounethenorthface.fr/ Doudoune North Face
http://www.michaelkorsborse.eu/ Michael Kors Borse Outlet
http://www.prada-purse.us/ Prada Handbags
http://www.supremehoodiestore.us/ Supreme Hoodie
http://www.timberlandshoes.co.uk/ Timberland UK
http://www.uggslippersoutlet.us/ UGG Boots
http://www.filaschuhe.de/ Fila Schuhe
http://www.pandora-canada.ca/ Pandora Rings
http://www.yeezymafia.us/ Yeezy Mafia Static
http://www.adidas-yeezy.de/ Adidas Schuhe
http://www.scarpenikeairmax.eu/ Nike Air Force
http://www.borsemichaelkors.eu/ Michael Kors
http://www.riverislandclothes.us/ River Island Shoes
http://www.adidasyeezyschuhe.de/ Adidas Jacke
http://www.suicoke-sandals.us/ Suicoke
http://www.thenorth-face.fr/ Doudoune The North Face
http://www.ralphlaurenshirt.org.uk/ Ralph Lauren
http://www.skecherssandals.co.uk/ Skechers UK
http://www.underarmour-outlet.ca/ Under Armour Canada
http://www.prada-canada.ca/ Prada
http://www.supremehoodie.org.uk/ Supreme Jacket
http://www.skechers-boots.us/ Skechers Shoes
http://www.underarmour.us.com/ Under Armour Outlet
http://www.scarpevans.eu/ Vans
http://www.vansshoes-outlet.us/ Vans
http://www.scarpesaucony.eu/ Scarpe Saucony Outlet
http://www.pumafentyshoes.us/ Puma Rihanna
http://www.underarmourtrainers.co.uk/ Under Armour
http://www.anellipandora.eu/ Collane Pandora
http://www.tommyhilfigerdresses.us/ Tommy Hilfiger Jacket
http://www.puma.org.uk/ Puma Shoes
http://www.swarovskijewelryoutlet.us/ Swarovski Jewelry
http://www.underarmourtracksuit.co.uk/ Under Armour
http://www.pandorajewelryoutlet.us.org/ Pandora
http://www.adidasschuheherren.de/ Yeezy Schuhe
http://www.yeezychaussureadidas.fr/ Adidas
http://www.ugg-uk.co.uk/ UGG UK
http://www.saucony-shoes.us/ Saucony Sneakers
http://www.superdryclothing.us/ Superdry
http://www.vans-shoes.ca/ Vans Old Skool
http://www.skechersoutletcanada.ca/ Skechers Boots
http://www.the-northface.us/ North Face Backpack
http://www.scarpeadidas.eu/ Adidas Yeezy
http://www.vibramshoes.us.com/ Vibram 5 Fingers
http://www.adidas-yeezy.fr/ Yeezy Boost
http://www.northface-jacke.de/ The North Face Jacke
http://www.pandorajewelryofficialsite.us/ Pandora Charms
http://www.superdryjackets.co.uk/ Superdry Jacket
http://www.thenorthface-jacke.de/ The North Face Schuhe
http://www.toryburchhandbags.us/ Tory Burch Crossbody
http://www.scarpe-hogan.eu/ Scarpe Hogan
http://www.salomonshoes.us/ Salomon Running Shoes
http://www.bijouxpandora2019.fr/ Pandora 2019
http://www.ralphlauren-poloshirts.us/ Ralph Lauren Dresses
http://www.converseallstar.fr/ Converse All Star
http://www.reeboks.us/ Reebok Classic
http://www.pandora-charms.ca/ Pandora Charms
http://www.swarovskicrystaloutlet.us/ Swarovski Outlet
http://www.riverislandshoes.co.uk/ River Island UK
http://www.pradapurse.us/ Prada Handbags
http://www.pandora-outlet.us/ Pandora Jewelry
http://www.schuhe-nike.de/ Nike Air Force
http://www.poloralph-lauren.us/ Ralph Lauren Outlet
http://www.salvatore-ferragamo.co.uk/ Salvatore Ferragamo
http://www.swarovskicrystalcanada.ca/ Swarovski Necklace
http://www.the-northface.org.uk/ North Face Backpack
http://www.pandoracharms-outlet.us/ Pandora Charms
http://www.salomonshoes.org.uk/ Salomon Shoes
http://www.bottes-ugg.fr/ UGG Pas Cher
http://www.sperryoutlet.us/ Sperrys Women
http://www.nikeschuheairmax.de/ Nike Air Force
http://www.offwhite-hoodie.us/ Off White Clothing
http://www.pandorajewelrycom.us/ Pandora
http://www.offwhiteshoes.org.uk/ Off White Shoes
http://www.uggslipperscanada.ca/ UGG Outlet
http://www.sperry.us.org/ Sperry Outlet
http://www.redbottomschristianlouboutin.us/ Louboutin
http://www.tommyhilfiger-outlet.us/ Tommy Hilfiger Jacket
karina님의 댓글
karina 작성일
http://www.vans-shoes.ca/ Vans
http://www.yeezys.eu/ Yeezy
http://www.anellipandora.eu/ Collane Pandora
http://www.scarpesaucony.eu/ Scarpe Saucony
http://www.reebok.org.uk/ Reebok
http://www.ultra-boost.us/ Adidas Shoes
http://www.skechersoutletcanada.ca/ Skechers Canada
http://www.tommyhilfiger-outlet.us/ Tommy Hilfiger
http://www.prada-purse.us/ Prada Purse
http://www.vansshoes.org.uk/ Vans Old Skool
http://www.uggbootsstore.us/ UGGS For Women
http://www.superdryclothing.us/ Superdry Jacket
http://www.offwhiteshoes.org.uk/ Off White Clothing
http://www.pumafentyshoes.us/ Puma Rihanna
http://www.salvatore-ferragamo.co.uk/ Salvatore Ferragamo
http://www.swarovskicrystaloutlet.us/ Swarovski Bracelet
http://www.pandorajewelrycom.us/ Pandora Earrings
http://www.pandorajewelryofficialsite.us/ Pandora
http://www.riverislanddresses.co.uk/ River Island Clothes
http://www.scarpehogan.eu/ Hogan Uomo
http://www.riverislandsale.co.uk/ River Island UK
http://www.borsemichaelkors.eu/ Borse Michael Kors
http://www.underarmour.us.com/ Under Armour Shoes
http://www.supremeclothingcanada.ca/ Supreme Shirt
http://www.pradapurse.us/ Prada Bags
http://www.underarmourtrainers.co.uk/ Under Armour Trainers
http://www.superdryjacket.us/ Superdry Hoodie
http://www.adidas-yeezy.de/ Adidas Ultra Boost
http://www.pandora-charms.ca/ Pandora Jewelry
http://www.balenciagaus.us/ Balenciaga Shoes
http://www.michaelkorsborse.eu/ Borse Michael Kors
http://www.pandora-outlet.us/ Pandora Jewelry
http://www.supremehoodie.org.uk/ Supreme Clothing
http://www.puma-shoes.co.uk/ Puma Suede
http://www.off-whiteshoes.us/ Off White Shoes
http://www.ralphlaurenshirt.org.uk/ Ralph Lauren Polo Shirts
http://www.offwhiteshirt.us/ Off White
http://www.pumarihannafenty.us/ Puma Suede
http://www.poloralph-lauren.us/ Polo Shirts
http://www.adidasschuheherren.de/ Adidas Ultra Boost
http://www.conversefemme.fr/ Converse Femme
http://www.schuhe-nike.de/ Nike Air Max
http://www.puma.org.uk/ Puma Sneakers
http://www.adidasyeezyschuhe.de/ Adidas Schuhe
http://www.swarovskicrystalcanada.ca/ Swarovski Necklace
http://www.scarpevans.eu/ Vans Scarpe
http://www.ralphlauren-poloshirts.us/ Ralph Lauren Outlet
http://www.swarovskijewelryoutlet.us/ Swarovski Crystal
http://www.yezzys.org.uk/ Yeezy
http://www.salvatoreferragamo.org.uk/ Salvatore Ferragamo Belt
http://www.salomonshoes.org.uk/ Salomon Hiking Boots
http://www.sperryoutlet.us/ Sperry
http://www.bapehoodieoutlet.us/ Bape Outlet
http://www.salomonshoes.us/ Salomon
http://www.offwhite-hoodie.us/ Off White Shoes
http://www.suicoke-sandals.us/ Suicoke Womens
http://www.supremeclothingshop.us/ Supreme Hoodie
http://www.pradabags.org.uk/ Prada Purse
http://www.superdryhoodie.co.uk/ Superdry Jacket
http://www.pandoracharms-outlet.us/ Pandora Outlet
http://www.timberlandshoes.co.uk/ Timberland Boots
http://www.underarmourtracksuit.co.uk/ Under Armour Tracksuit
http://www.toryburch-outlet.us/ Tory Burch
http://www.tommyhilfigerdresses.us/ Tommy Hilfiger Outlet
http://www.air-max.fr/ Shaussure Nike
http://www.thenorthface-jacke.de/ The North Face Jacke
http://www.bijouxpandora2019.fr/ Pandora
http://www.pandorajewelryoutlet.us.org/ Pandora
http://www.riverislandshoes.co.uk/ River Island
http://www.redbottomschristianlouboutin.us/ Christian Louboutin Shoes
http://www.vans-canada.ca/ Vans Old Skool
http://www.pandoraringsuk.co.uk/ Pandora
http://www.skecherssandals.co.uk/ Skechers UK
http://www.vansshoes-outlet.us/ High Top Vans
http://www.underarmour-outlet.ca/ Under Armour Shoes
http://www.riverislandclothes.us/ River Island Clothes
http://www.bottes-ugg.fr/ UGG Outlet
http://www.doudounethenorthface.fr/ The North Face
http://www.yeezyboost350.fr/ Yeezy Boost
http://www.scarpeadidas.eu/ Adidas Scarpe
http://www.chaussurenikeofficiel.fr/ Chaussure Nike
http://www.skechers-boots.us/ Skechers Go Walk
http://www.supremeclothing-uk.co.uk/ Supreme Jacket
http://www.timberlandbootsstore.us/ Timberland Boots
http://www.nikeschuheairmax.de/ Nike Air Max
http://www.vibramshoes.us.com/ Vibram Shoes
http://www.reeboks.us/ Reebok Classic
http://www.superdryjackets.co.uk/ Superdry Sale
http://www.adidas-yeezy.fr/ Yeezy Boost 350
http://www.pandora-canada.ca/ Pandora Charms
http://www.tomsboots.us/ Toms Sale
http://www.stevemaddensneakers.us/ Steve Madden Slip Ons
http://www.uggslippersoutlet.us/ UGGS On Sale
http://www.reebok-classic.us/ Reebok Shoes
http://www.uggslipperscanada.ca/ UGG
http://www.yeezychaussureadidas.fr/ Basket Adidas
http://www.filaschuhe.de/ Fila
http://www.northface-jacke.de/ North Face Jacke
http://www.supremehoodiestore.us/ Supreme Clothing
http://www.the-northface.org.uk/ North Face UK
http://www.valentinosandals.us/ Valentino Heels
http://www.sperry.us.org/ Sperrys Men
http://www.puma-canada.ca/ Puma Shoes Canada
http://www.toryburchhandbags.us/ Tory Burch Outlet
http://www.ugg-uk.co.uk/ UGG Boots Sale
http://www.yeezymafia.us/ Adidas Yeezy
http://www.prada-canada.ca/ Prada Bags
http://www.thenorth-face.fr/ Veste North Face
http://www.pumaschuhedamen.de/ Puma Suede
http://www.converseallstar.fr/ Converse Femme
http://www.scarpe-hogan.eu/ Scarpe Hogan Uomo
http://www.scarpenikeairmax.eu/ Scarpe Nike
http://www.vibramshoes.us/ Vibram Boots
http://www.saucony-shoes.us/ Saucony
http://www.the-northface.us/ North Face
jennifer님의 댓글
jennifer 작성일
http://www.pandoracanadacharms.ca/ pandora rings
http://www.salomonboots.co.uk/ salomon
http://www.pandora--jewelry.us.org/ pandora charms
http://www.longchampbag.us.com/ longchamp backpack
http://www.jordan11spacejams.us.com/ space jam 11
http://www.balenciaga.us.org/ balenciaga
http://www.air-max.us/ nike air max 90
http://www.kate-spadepurses.us/ kate spade
http://www.eccoshoesoutlets.us.com/ ecco boots
http://www.adidasyeezyshoes.co.uk/ yeezy boost 350
http://www.hermesbirkin-handbags.us.com/ Hermes Belts
http://www.jordan11.us.com/ jordan shoes
http://www.yeezyboost350shoes.us.com/ yeezy
http://www.skechers-store.com/ Skechers Outlet
http://www.pandoras-jewelrys.us.com/ pandora
http://www.birkenstocksandalssale.us.com/ birkenstock
http://www.moncler-coat.us.com/ moncler
http://www.lebron15-shoes.us.com/ lebron 15
http://www.salvatore-ferragamo.us.com/ ferragamo shoes
http://www.birkenstockshop.us/ Birkenstock
http://www.yeezytrainers.org.uk/ Adidas NMD
http://www.offwhitestore.us/ Off White Sneakers
http://www.redbottomslouboutinshoes.us.com/ red bottoms
http://www.burberrys.org.uk/ burberry scarf
http://www.moncler-uk.co.uk/ moncler
http://www.james-hardenshoes.us.com/ james harden shoes
http://www.lebron-16shoes.us/ lebron 15
http://www.fitflops-sale.us.com/ fitflop sale
http://www.pandorajewelryscharms.us.com/ pandora jewelry official site
http://www.curry-5shoes.us/ curry 4
http://www.monclerjacketwomens.us.com/ moncler coat
http://www.christianlouboutins.ca/ christian louboutin shoes
http://www.vans--shoes.us.com/ vans
http://www.kd10-shoes.us.com/ kd 9
http://www.nikeairmax-90.us.com/ Nike Air vapormax
http://www.nikeair-max90.co.uk/ nike air max 95
http://www.katespade-bags.us/ kate spade
http://www.katespadepurses.us.com/ kate spade handbags
http://www.yeezyboost-350v2.fr/ yeezy boost 350
http://www.salomonshoes.ca/ salomon speedcross 4
http://www.mizunos.us/ mizuno running shoes
http://www.yeezy-950.us/ yeezy 950
http://www.monclers.uk/ moncler
http://www.pandorajewelryrings.us.com/ pandora earrings
http://www.monclers.us.com/ moncler coat
http://www.longchampbackpack.us.com/ longchamp
http://www.goyardhandbags.us/ goyard bag
http://www.airmax90shoes.us.com/ nike air max 2018
http://www.louboutin-shoesuk.co.uk/ louboutin shoes
http://www.goyardbag.us.com/ goyard bag
http://www.nmd.us.org/ nmd
http://www.jordan11shoes.us.com/ jordan 11 space jam
http://www.adidas-ultraboost.us.com/ yeezy boost
http://www.katespadebags.us.com/ kate spade bags
http://www.adidascanada-shoes.ca/ adidas outlet
http://www.katespades.ca/ kate spade outlet
http://www.pandorauk.us.com/ pandora jewelry
http://www.giuseppezanottis.us/ giuseppe shoes
http://www.nikelebron15.us.com/ lebron shoes
http://www.goldengoosesneakerssale.us/ golden goose sneakers
http://www.pandora-charmsjewelry.us.com/ pandora bracelet
http://www.adidas--yeezy.co.uk/ yeezy 350
http://www.pumarihannafenty.us.com/ rihanna fenty puma
http://www.fitflop-shoes.ca/ fitflop shoes
http://www.salomonspeedcross3.us.com/ salomon xa pro 3d
http://www.redbottom-shoes.co.uk/ louboutin
http://www.katespades.co.uk/ kate spade purses
http://www.christianlouboutin-store.us/ Red Bottom Shoes
http://www.yeezy-750.us/ yeezy boost 750
http://www.jordans11shoes.us.com/ air jordan
http://www.philipppleins.us/ philipp plein shoes
http://www.ed-hardys.us.com/ ed hardy shirt
http://www.yeezy-500.us/ yeezy 500
http://www.adidastrainers-uk.co.uk/ adidas trainers
http://www.fitflopsshoes.us.com/ fitflop
http://www.birkenstock-uk.org.uk/ Birkenstock Sandals
http://www.mizuno-shoes.us/ mizuno
http://www.fjallravenstore.us/ Fjallraven Bags
http://www.hydroflaskstore.us/ Hydro Flask Sale
http://www.nike-trainersuk.co.uk/ Nike Air Max
http://www.louboutinredbottoms.us.com/ christian louboutin
http://www.golden-goosesneakers.us.com/ golden goose
http://www.goldengoosesale.us/ golden goose outlet
http://www.filas.us.org/ fila shoes womens
http://www.nikeoffwhiteshoes.us/ nike off white
http://www.adidasnmdrunnerr1.us.com/ adidas nmd r1
http://www.coachbags-outlet.us.com/ coach bags
http://www.nike-canada.ca/ nike shoes
http://www.karenmillenstore.us/ Karen Millen Dresses
http://www.yeezy.in.net/ yeezy boost 350
http://www.uggsforwomen.us/ ugg slippers
http://www.bapestore.us/ Bape Clothing
http://www.salomon.us.org/ salomon xa pro 3d
http://www.redbottoms-shoes.us.org/ red bottoms
http://www.ralphlauren-store.us/ Ralph Lauren
http://www.airjordan11spacejam.us.com/ air jordan
http://www.monclerjacket.org.uk/ moncler
http://www.christianlouboutinredbottoms.us.com/ christian louboutin
http://www.philipppleinoutlet.us/ philipp plein
http://www.adidasyeezy-350.us.com/ yeezy shoes
http://www.pandora-jewelrysale.us.com/ pandora charms
http://www.nikeairvapormaxflyknit.us.com/ nike air max 90
http://www.pandora-bracelet.fr/ bague pandora
http://www.vapormaxs.us.com/ nike air vapormax flyknit
http://www.red-bottoms.us.org/ christian louboutin
http://www.fila-shoes.us/ fila shoes
http://www.fjallravenkanken-backpack.us/ fjallraven
http://www.goyard.org.uk/ goyard
http://www.nike--shoes.co.uk/ nike air max 97
http://www.yeezy--shoes.co.uk/ yeezy boost 350 v2
ronald님의 댓글
ronald 작성일
http://www.calvinkleinunderwear.org.uk/ Calvin Klien
http://www.lebron-17.us/ Nike Lebron 17
http://www.giuseppe.org.uk/ Giuseppe Zanotti Trainers
http://www.canadagoosejacketsoutlet.us/ Canada Goose Coat
http://www.northfaceoutlet.co.uk/ The North Face
http://www.balenciaga-shoes.ca/ Balenciaga Bags
http://www.calvin-klein.org.uk/ Calvin Klein Underwear
http://www.bapeclothing.co.uk/ Bape Clothing
http://www.fjallravenkanken.ca/ Fjallraven Kanken Backpack
http://www.ecco-shoes.ca/ Ecco
http://www.fendibags.us/ Fendi Bags
http://www.goyard-bags.co.uk/ Goyard
http://www.bose.org.uk/ Bose Wireless Headphones
http://www.juicycoutureoutlet.us/ Juicy Couture Bags
http://www.northfacejacketsoutlet.us/ North Face Jacket
http://www.katespadenewyork.us/ Kate Spade Bags
http://www.laurenralphlauren.us/ Polo Ralph Lauren
http://www.fjallravenkankenofficialsite.us/ Fjallraven Kanken Official Site
http://www.airmax270sale.us/ Nike Air Max
http://www.goyardbagsstore.us/ Goyard Wallet
http://www.filaclothing.us/ Fila Sneakers
http://www.converse-canada.ca/ Converse High Tops
http://www.air-max720.us/ Nike Air Max
http://www.ferragamos.us/ Ferragamo
http://www.fjallraven-kanken.org.uk/ Fjallraven
http://www.hydroflask-sale.us/ Hydro Flask Sale
http://www.championhoodie.org.uk/ Champion Hoodie
http://www.fila-canada.ca/ Fila Canada
http://www.mcmbackpackbags.us/ MCM
http://www.coachbags.org.uk/ Coach Handbags UK
http://www.airmax90.co.uk/ Air Max 90
http://www.north-facejacket.us/ The North Face
http://www.birkenstocksale.org.uk/ Birkenstock Sandals
http://www.nikeuk-trainers.org.uk/ Nike Shoes
http://www.bose-wirelessheadphones.us/ Bose Wireless Headphones
http://www.jordan-shoes.ca/ Nike Jordan
http://www.longchamp.org.uk/ Longchamp
http://www.nike-shoes.org.uk/ Nike Trainers
http://www.championsweatshirt.co.uk/ Champion T Shirt
http://www.birkenstocksandals.ca/ Birkenstock Shoes
http://www.jackwolfskin.org.uk/ Jack Wolfskin Fleece
http://www.birkenstocksandals-sale.us/ Birkenstock Sale
http://www.airmax2020.us/ Air Max 720
http://www.championtshirt.us/ Champion Hoodie
http://www.adidas-zxflux.us/ Adidas Stan Smith
http://www.adidasstasmith.us/ Adidas Superstar
http://www.bapeshirt.us.com/ Bape Sweater
http://www.jordan-11.us.com/ Jordan Retro 11
http://www.canadgoosejacket.us/ Canada Goose Coat
http://www.lululemonpants.ca/ Lululemon
http://www.lululemons.us/ Lululemon Leggings
http://www.boseheadphones.ca/ Bose Soundlink
http://www.karenmillenuk.org.uk/ Karen Millen
http://www.asicscanadashoes.ca/ Asics Gel Kayano
http://www.air-max90.us/ Nike UK
http://www.bottegaveneta-handbags.us/ Bottega Veneta Handbags
http://www.clarks-outlet.co.uk/ Clarks Sandals
http://www.championsweatshirt.us/ Champion Sweatshirt
http://www.asicstrainers.co.uk/ Asics Trainers
http://www.adidascanadaoutlet.ca/ Adidas Shoes
http://www.monclersale.us/ Moncler T Shirt
http://www.mizunousa.us/ Mizuno USA
http://www.canadagoosejacketuk.co.uk/ Canada Goose Sale
http://www.filashoes.org.uk/ Fila Trainers
http://www.northfacebackpack.us/ North Face
http://www.karenmillendresses.us/ Karen Millen Outlet
http://www.converseshoes-outlet.us/ Converse Outlet
http://www.hydroflaskuk.co.uk/ Hydro Flask
http://www.champion-hoodie.us/ Champion Sweatshirt
http://www.katespade-bags.ca/ Kate Spade
http://www.balenciagas.org.uk/ Balenciaga Trainers
http://www.coachbags-outlet.us/ Coach Outlet
http://www.christianlouboutinheels.us/ Christian Louboutin Heels
http://www.lacoste-shoes.us/ Lacoste Shoes
http://www.filashoesshirt.us/ Fila Shirt
http://www.bapehoodie.org.uk/ A Bathing Ape
http://www.airmax270.ca/ Nike Air Max
http://www.burberry-scarf.co.uk/ Burberry UK
http://www.karenmillenoutlet.us/ Karen Millen Skirts
http://www.columbiajackets.us/ Columbia Jacket
http://www.goldengoose-sale.us/ Golden Goose
http://www.karenmillendresses.org.uk/ Karen Millen UK
http://www.ferragamoshoes.ca/ Ferragamo
http://www.conversetrainers.co.uk/ Converse High Tops
http://www.adidas-yeezy.ca/ Yeezy Boost 350
http://www.fjallraven-backpack.us/ Fjallraven Kanken
http://www.balenciagashoes.org.uk/ Balenciaga Bags
http://www.brooks-shoes.us/ Brooks Shoes
http://www.boseheadphonesstore.us/ Bose Earphones
http://www.adidasshoes.org.uk/ Adidas Hoodie
http://www.michaelkors-purse.us/ Michael Kors Outlet
http://www.hugobossjeans.us/ Hugo Boss Suits
http://www.converseallstar.us/ Converse
http://www.katespadebags.org.uk/ Kate Spade Purses
http://www.katespadebags.co.uk/ Kate Spade Wallet
http://www.lululemonleggingsoutlet.us/ Lululemon Leggings
http://www.giuseppe-shoes.us/ Giuseppe Zanotti
http://www.nikecanadaoutlet.ca/ Air Max
http://www.jackwolfskinjackets.org.uk/ Jack Wolfskin
http://www.adidas-yeezy.co.uk/ Yeezy Shoes
http://www.calvinklein-dresses.us/ Calvin Klein Shoes
http://www.adidasyeezy.us/ Yeezy 500
http://www.bvlgari-jewelry.us/ Bvlgari Earrings
http://www.hydroflaskwaterbottle.us/ Hydro Flask 32 OZ
http://www.clark-shoes.us/ Clarks Boots
http://www.fjallravenbackpack.co.uk/ Fjallraven Kanken Backpack
http://www.fitflop-sandals.us/ Fitflop
http://www.curry6-shoes.us/ Curry 6
http://www.eccosandals.us/ Ecco Boots
http://www.birkenstocksale.co.uk/ Birkenstock Shoes
http://www.clarks-canada.ca/ Clarks Wallabees
http://www.katespade-canada.ca/ Kate Spade Outlet
http://www.longchampbackpackbags.us/ Longchamp Bags
http://www.monclercoat.co.uk/ Moncler Coat
http://www.birkenstocksandals-outlet.us/ Birkenstock Sandals
http://www.fitflopshoes.co.uk/ Fitflop UK
http://www.merrell-shoes.us/ Merrell Hiking Shoes
http://www.cartier-lovebracelet.us/ Cartier Ring
http://www.bosestore.us/ Bose Bluetooth Speaker
http://www.hydro-flask.org.uk/ Hydro Flask Sale
http://www.championhoodie.ca/ Champion Hoodie Canada
http://www.montblancpensoutlet.us/ Mont Blanc Ballpoint Pen
http://www.hydroflasks.ca/ Hydro Flask Lids
http://www.goldengoose.org.uk/ Golden Goose Sneakers Sale
http://www.boseheadphones.co.uk/ Bose Soundlink Mini
http://www.bapehoodie.ca/ Bape Shirt
http://www.mont-blanc.org.uk/ Mont Blanc Pens
http://www.jordan-11.org.uk/ Jordan Shoes
http://www.coachpurses.us/ Coach Handbags
http://www.burberrybags.org.uk/ Burberry UK
http://www.asicswomensshoes.us/ Asics Shoes
http://www.bose-canada.ca/ Bose Canada
http://www.eccoshoes-outlet.us/ Ecco Shoes
http://www.hugobosssuits.us/ Hugo Boss Shoes
http://www.northfacejackets.org.uk/ North Face
http://www.canadagoose-jacket.ca/ Canada Goose Coat
http://www.monclerjacketwomens.us/ Moncler T Shirt
http://www.michaelkorshandbagsoutlet.us/ Michael Kors
http://www.jordan-33.us/ Jordan Retro 11
http://www.louboutintrainers.org.uk/ Christian Louboutin Shoes
http://www.juicycouturetracksuit.us/ Juicy Couture Outlet
http://www.columbiaclothing.us/ Columbia Coats
http://www.goldengoosesneakerssale.co.uk/ Golden Goose Sneakers
http://www.lacosteoutlet.us/ Lacoste Shirts
http://www.goldengoosetrainers.co.uk/ Golden Goose Sneakers Sale
http://www.goyardbags.org.uk/ Goyard Tote
http://www.addidasnmd.us/ Adidas Yeezy
http://www.cartiercanada.ca/ Cartier Love Ring
http://www.merrellboots.us/ Merrell Boots
http://www.asicsrunningshoes.co.uk/ Asics Kayano
http://www.champion-sweatshirt.us/ Champion Sweatshirt
http://www.fitflopshoessandals.us/ Fitflop Sandals
http://www.fendishoes.us/ Fendi Clothing
http://www.calvinkleincanada.ca/ Calvin Klein Canada
http://www.montblancpens.org.uk/ Mont Blanc Pen
marianne님의 댓글
marianne 작성일
http://www.columbiaclothing.us/ Columbia
http://www.goldengoose-sale.us/ Golden Goose Shoes
http://www.coachbags-outlet.us/ Coach Purses
http://www.northfaceoutlet.co.uk/ North Face Backpack
http://www.hydro-flask.org.uk/ Hydro Flask Sale
http://www.fitflopshoessandals.us/ Fitflop Shoes
http://www.eccosandals.us/ Ecco
http://www.birkenstocksale.org.uk/ Birkenstock Sale
http://www.north-facejacket.us/ North Face Coats
http://www.airmax2020.us/ Air Max 2020
http://www.bosestore.us/ Bose
http://www.fendibags.us/ Fendi Shirt
http://www.katespadebags.org.uk/ Kate Spade Handbags
http://www.birkenstocksandals.ca/ Birkenstock Sandals
http://www.merrell-shoes.us/ Merrell Shoes
http://www.longchampbackpackbags.us/ Longchamp
http://www.michaelkorshandbagsoutlet.us/ Michael Kors Handbags
http://www.jordan-33.us/ Jordan Shoes
http://www.adidas-yeezy.ca/ Adidas Yeezy
http://www.curry6-shoes.us/ Curry Shoes
http://www.goyard-bags.co.uk/ Goyard Handbags
http://www.championsweatshirt.us/ Champion Sweatshirt
http://www.northfacebackpack.us/ North Face Outlet
http://www.calvinklein-dresses.us/ Calvin Klein Jeans
http://www.bapeshirt.us.com/ Bape Hoodie
http://www.filashoesshirt.us/ Fila
http://www.monclersale.us/ Moncler Jacket
http://www.monclerjacketwomens.us/ Moncler Womens
http://www.hugobossjeans.us/ Hugo Boss Jacket
http://www.boseheadphones.co.uk/ Bose Soundlink Mini
http://www.fila-canada.ca/ Fila Hoodie
http://www.air-max90.us/ Air Max 95
http://www.fjallraven-backpack.us/ Fjallraven Kanken Backpack
http://www.columbiajackets.us/ Columbia Outlet
http://www.ferragamos.us/ Salvatore Ferragamo
http://www.balenciagashoes.org.uk/ Balenciagas
http://www.boseheadphonesstore.us/ Bose Earphones
http://www.hydroflasks.ca/ Hydro Flask Canada
http://www.champion-hoodie.us/ Champion Sweatshirt
http://www.monclercoat.co.uk/ Moncler Outlet
http://www.hydroflaskuk.co.uk/ Hydro Flask UK
http://www.calvinkleinunderwear.org.uk/ Calvin Klein Dresses
http://www.jordan-shoes.ca/ Jordan 13
http://www.lebron-17.us/ Lebron James Shoes
http://www.birkenstocksandals-outlet.us/ Birkenstock
http://www.katespadebags.co.uk/ Kate Spade Handbags
http://www.balenciaga-shoes.ca/ Balenciagas
http://www.burberrybags.org.uk/ Burberry Scarf
http://www.lacosteoutlet.us/ Lacoste Shirts
http://www.conversetrainers.co.uk/ Converse UK
http://www.karenmillenoutlet.us/ Karen Millen Outlet
http://www.calvinkleincanada.ca/ Calvin Klein Dresses
http://www.filashoes.org.uk/ Fila Sweatshirt
http://www.adidascanadaoutlet.ca/ Adidas Canada
http://www.katespade-canada.ca/ Kate Spade Handbags
http://www.goyardbags.org.uk/ Goyard Handbags
http://www.goyardbagsstore.us/ Goyard Bags
http://www.bapehoodie.org.uk/ Bape Jacket
http://www.airmax270sale.us/ Nike Air Max
http://www.katespade-bags.ca/ Kate Spade Outlet
http://www.giuseppe-shoes.us/ Giuseppe
http://www.goldengoosetrainers.co.uk/ Golden Goose Trainers
http://www.mcmbackpackbags.us/ MCM Bags
http://www.bose-canada.ca/ Bose Soundlink
http://www.karenmillenuk.org.uk/ Karen Millen
http://www.northfacejackets.org.uk/ The North Face
http://www.championhoodie.ca/ Champion Sweatshirt
http://www.mizunousa.us/ Mizuno
http://www.airmax90.co.uk/ Air Max 90
http://www.balenciagas.org.uk/ Balenciaga
http://www.montblancpensoutlet.us/ Mont Blanc Fountain Pen
http://www.asicstrainers.co.uk/ Asics Outlet
http://www.champion-sweatshirt.us/ Champion Clothing
http://www.bapehoodie.ca/ Bape Shirt
http://www.adidasstasmith.us/ Stan Smith Shoes
http://www.clarks-outlet.co.uk/ Clarks Shoes
http://www.merrellboots.us/ Merrell Outlet
http://www.coachpurses.us/ Coach Bags
http://www.jackwolfskin.org.uk/ Jack Wolfskin Jacket
http://www.ferragamoshoes.ca/ Salvatore Ferragamo Shoes
http://www.fjallravenkankenofficialsite.us/ Fjallraven Kanken
http://www.hydroflask-sale.us/ Hydro Flask
http://www.converseshoes-outlet.us/ Converse All Star
http://www.eccoshoes-outlet.us/ Ecco Shoes
http://www.bapeclothing.co.uk/ Bape Shirt
http://www.goldengoosesneakerssale.co.uk/ Golden Goose
http://www.brooks-shoes.us/ Brooks Running Shoes
http://www.adidasshoes.org.uk/ Adidas Sweatshirt
http://www.nikeuk-trainers.org.uk/ Nike UK
http://www.asicsrunningshoes.co.uk/ Asics
http://www.nikecanadaoutlet.ca/ Air Max 97
http://www.canadgoosejacket.us/ Canada Goose Jacket
http://www.adidas-yeezy.co.uk/ Yeezy
http://www.converse-canada.ca/ Converse High Tops
http://www.canadagoosejacketuk.co.uk/ Canada Goose Parka
http://www.montblancpens.org.uk/ Mont Blanc Fountain Pen
http://www.juicycouturetracksuit.us/ Juicy Couture
http://www.christianlouboutinheels.us/ Red Bottoms
http://www.lululemonleggingsoutlet.us/ Lululemon Outlet
http://www.fjallravenbackpack.co.uk/ Fjallraven Kanken Backpack
http://www.filaclothing.us/ Fila Shirt
http://www.michaelkors-purse.us/ Michael Kors Handbags
http://www.northfacejacketsoutlet.us/ North Face Jacket
http://www.championtshirt.us/ Champion Shoes
http://www.fjallravenkanken.ca/ Fjallraven Canada
http://www.jordan-11.org.uk/ Jordan 12
http://www.championhoodie.org.uk/ Champion Sweatshirt
http://www.bottegaveneta-handbags.us/ Bottega Veneta Handbags
http://www.fitflop-sandals.us/ Fitflop Slippers
http://www.clarks-canada.ca/ Clarks Sandals
http://www.hydroflaskwaterbottle.us/ Hydro Flask 32 OZ
http://www.lululemonpants.ca/ Lululemon
http://www.canadagoosejacketsoutlet.us/ Canada Goose Jacket
http://www.calvin-klein.org.uk/ Calvin Klein Dresses
http://www.cartier-lovebracelet.us/ Cartier Bracelet
http://www.hugobosssuits.us/ Hugo Boss Shoes
http://www.canadagoose-jacket.ca/ Canada Goose Jacket
http://www.giuseppe.org.uk/ Giuseppe Zanotti
http://www.lacoste-shoes.us/ Lacoste Shoes
http://www.converseallstar.us/ Converse Shoes
http://www.fjallraven-kanken.org.uk/ Fjallraven Backpack
http://www.championsweatshirt.co.uk/ Champion Tracksuit
http://www.adidas-zxflux.us/ Adidas Gazelle
http://www.bose.org.uk/ Bose Headphones
http://www.jordan-11.us.com/ New Jordans
http://www.burberry-scarf.co.uk/ Burberry
http://www.nike-shoes.org.uk/ Nike UK
http://www.goldengoose.org.uk/ Golden Goose Sneakers
http://www.birkenstocksandals-sale.us/ Birkenstock
http://www.addidasnmd.us/ NMD
http://www.laurenralphlauren.us/ Polo Ralph Lauren
http://www.air-max720.us/ Air Max 720
http://www.cartiercanada.ca/ Cartier Love Bracelet
http://www.longchamp.org.uk/ Longchamp Bags
http://www.lululemons.us/ Lululemon Yoga Mat
http://www.coachbags.org.uk/ Coach Purses
http://www.karenmillendresses.org.uk/ Karen Millen Outlet
http://www.adidasyeezy.us/ Yeezy 500
http://www.mont-blanc.org.uk/ ont Blanc Pen
http://www.fitflopshoes.co.uk/ Fitflop Shoes
http://www.katespadenewyork.us/ Kate Spade New York
http://www.birkenstocksale.co.uk/ Birkenstock Sandals
http://www.jackwolfskinjackets.org.uk/ Jack Wolfskin Coat
http://www.boseheadphones.ca/ Bose Speakers
http://www.bose-wirelessheadphones.us/ Bose Headphones
http://www.ecco-shoes.ca/ Ecco Canada
http://www.asicswomensshoes.us/ Asics Womens Shoes
http://www.bvlgari-jewelry.us/ Bvlgari Bracelet
http://www.fendishoes.us/ Fendi Shirt
http://www.airmax270.ca/ Nike Air Max 270
http://www.karenmillendresses.us/ Karen Millen Skirts
http://www.louboutintrainers.org.uk/ Red Bottoms
http://www.asicscanadashoes.ca/ Asics Gel Kayano
http://www.clark-shoes.us/ Clarks Boots
http://www.juicycoutureoutlet.us/ Juicy Couture Handbags
jerry님의 댓글
jerry 작성일
http://www.supremehoodiestore.us/ Supreme Clothing
http://www.sperry.us.org/ Sperry
http://www.filaschuhe.de/ Fila Disruptor
http://www.supremeclothingshop.us/ Supreme Coats
http://www.underarmourtrainers.co.uk/ Under Armour
http://www.yeezychaussureadidas.fr/ Adidas
http://www.skechersoutletcanada.ca/ Skechers Boots
http://www.vans-canada.ca/ Vans Slip On
http://www.pumarihannafenty.us/ Puma Suede
http://www.uggbootsstore.us/ UGG Slippers
http://www.northface-jacke.de/ North Face Jacke
http://www.puma-canada.ca/ Puma Rihanna
http://www.puma.org.uk/ Puma Suede
http://www.vibramshoes.us.com/ Vibram 5 Fingers
http://www.anellipandora.eu/ Anelli Pandora
http://www.riverislandshoes.co.uk/ River Island UK
http://www.pandoracharms-outlet.us/ Pandora
http://www.salomonshoes.us/ Salomon Running Shoes
http://www.underarmour-outlet.ca/ Under Armour Stock
http://www.pandoraringsuk.co.uk/ Pandora UK
http://www.converseallstar.fr/ Converse Pas Cher
http://www.uggslippersoutlet.us/ UGGS On Sale
http://www.pandorajewelryoutlet.us.org/ Pandora Charms
http://www.tommyhilfiger-outlet.us/ Tommy Hilfiger Outlet
http://www.pandora-outlet.us/ Pandora Charms
http://www.pumafentyshoes.us/ Puma Suede
http://www.underarmourtracksuit.co.uk/ Under Armour Trainers
http://www.balenciagaus.us/ Balenciaga Shoes
http://www.yezzys.org.uk/ Yezzys
http://www.ultra-boost.us/ Adidas Ultra Boost
http://www.ralphlauren-poloshirts.us/ Ralph Lauren
http://www.scarpesaucony.eu/ Scarpe Running
http://www.swarovskicrystalcanada.ca/ Swarovski Crystal
http://www.vansshoes-outlet.us/ Vans
http://www.pandora-charms.ca/ Pandora
http://www.pandorajewelrycom.us/ Pandora Earrings
http://www.riverislanddresses.co.uk/ River Island Shoes
http://www.pumaschuhedamen.de/ Puma Schuhe Damen
http://www.puma-shoes.co.uk/ Puma Suede Trainers
http://www.ralphlaurenshirt.org.uk/ Ralph Lauren Polo Shirts
http://www.supremeclothingcanada.ca/ Supreme Clothing
http://www.adidas-yeezy.fr/ Yeezy Boost
http://www.yeezyboost350.fr/ Yeezy
http://www.suicoke-sandals.us/ Suicoke Sandals
http://www.offwhiteshirt.us/ Nike Off White
http://www.ugg-uk.co.uk/ UGGS On Sale
http://www.schuhe-nike.de/ Schuhe Nike
http://www.conversefemme.fr/ Converse Pas Cher
http://www.pradapurse.us/ Prada Bags
http://www.superdryclothing.us/ Superdry Clothing
http://www.saucony-shoes.us/ Saucony Sneakers
http://www.toryburch-outlet.us/ Tory Burch Bags
http://www.valentinosandals.us/ Valentino Sandals
http://www.underarmour.us.com/ Under Armour Sweatshirt
http://www.scarpenikeairmax.eu/ Scarpe Nike
http://www.vibramshoes.us/ Vibram Shoes
http://www.adidasschuheherren.de/ Adidas Ultra Boost
http://www.timberlandshoes.co.uk/ Timberland Boots
http://www.redbottomschristianlouboutin.us/ Red Bottoms
http://www.prada-canada.ca/ Prada Shoes
http://www.vans-shoes.ca/ Vans
http://www.bapehoodieoutlet.us/ Bape Outlet
http://www.reeboks.us/ Reebok Outlet
http://www.chaussurenikeofficiel.fr/ Nike Chaussure
http://www.superdryjacket.us/ Superdry Jacket
http://www.skecherssandals.co.uk/ Skechers UK
http://www.offwhite-hoodie.us/ Off White Shirt
http://www.pradabags.org.uk/ Prada Purse
http://www.doudounethenorthface.fr/ The North Face
http://www.thenorth-face.fr/ Veste The North Face
http://www.poloralph-lauren.us/ Polo Ralph Lauren
http://www.salomonshoes.org.uk/ Salomon Hiking Boots
http://www.tommyhilfigerdresses.us/ Tommy Hilfiger Sweatshirt
http://www.adidasyeezyschuhe.de/ Adidas Yeezy
http://www.vansshoes.org.uk/ Vans Trainers
http://www.yeezys.eu/ Yeezy Boost 350 V2
http://www.off-whiteshoes.us/ Off White Belt
http://www.bijouxpandora2019.fr/ Bijoux Pandora
http://www.toryburchhandbags.us/ Tory Burch Purse
http://www.swarovskicrystaloutlet.us/ Swarovski Jewelry
http://www.stevemaddensneakers.us/ Steve Madden Slip Ons
http://www.supremehoodie.org.uk/ Supreme New York
http://www.uggslipperscanada.ca/ UGG Boots
http://www.bottes-ugg.fr/ Boots UGG
http://www.the-northface.us/ North Face Jacket
http://www.michaelkorsborse.eu/ Michael Kors Borse Outlet
http://www.prada-purse.us/ Prada Handbags
http://www.superdryjackets.co.uk/ Superdry
http://www.supremeclothing-uk.co.uk/ Supreme Outlet
http://www.tomsboots.us/ Toms Boots
http://www.timberlandbootsstore.us/ Timberland
http://www.scarpeadidas.eu/ Yeezy Boost 350 V2
http://www.salvatore-ferragamo.co.uk/ Ferragamo
http://www.reebok-classic.us/ Reebok Sneakers
http://www.yeezymafia.us/ Adidas Yeezy
http://www.salvatoreferragamo.org.uk/ Ferragamo Shoes
http://www.scarpevans.eu/ Vans Old School
http://www.reebok.org.uk/ Reebok Shoes
http://www.sperryoutlet.us/ Sperry Outlet
http://www.scarpehogan.eu/ Hogan Sneakers
http://www.pandorajewelryofficialsite.us/ Pandora Jewelry
http://www.adidas-yeezy.de/ Yeezy Schuhe
http://www.offwhiteshoes.org.uk/ Off White Hoodie
http://www.riverislandclothes.us/ River Island Dresses
http://www.nikeschuheairmax.de/ Air Max
http://www.scarpe-hogan.eu/ Hogan Donne
http://www.pandora-canada.ca/ Pandora
http://www.riverislandsale.co.uk/ River Island Shoes
http://www.borsemichaelkors.eu/ Borse Michael Kors
http://www.swarovskijewelryoutlet.us/ Swarovski Crystal
http://www.air-max.fr/ Shaussure Nike
http://www.superdryhoodie.co.uk/ Superdry Hoodie
http://www.thenorthface-jacke.de/ The North Face Schuhe
http://www.skechers-boots.us/ Skechers Shoes
http://www.the-northface.org.uk/ The North Face
ronald님의 댓글
ronald 작성일
http://www.supremehoodiestore.us/ Supreme
http://www.timberlandbootsstore.us/ Timberland Outlet
http://www.pandorajewelryoutlet.us.org/ Pandora Jewelry
http://www.timberlandshoes.co.uk/ Timberland UK
http://www.supremeclothingcanada.ca/ Supreme Clothing
http://www.michaelkorsborse.eu/ Borse Michael Kors
http://www.ralphlaurenshirt.org.uk/ Ralph Lauren Shirt
http://www.chaussurenikeofficiel.fr/ Air Max 95
http://www.superdryclothing.us/ Superdry Coats
http://www.reebok.org.uk/ Reebok Shoes
http://www.scarpe-hogan.eu/ Hogan Uomo
http://www.sperry.us.org/ Sperry
http://www.bapehoodieoutlet.us/ Bape Clothing
http://www.pandorajewelrycom.us/ Pandora
http://www.ultra-boost.us/ Adidas Ultra Boost
http://www.the-northface.org.uk/ North Face UK
http://www.adidas-yeezy.fr/ Yeezy Boost 350
http://www.poloralph-lauren.us/ Ralph Lauren Outlet
http://www.puma-shoes.co.uk/ Puma Sneakers
http://www.toryburchhandbags.us/ Tory Burch Outlet
http://www.reeboks.us/ Reebok
http://www.puma.org.uk/ Puma Suede Trainers
http://www.vans-shoes.ca/ Vans Shoes
http://www.valentinosandals.us/ Valentino Heels
http://www.pumaschuhedamen.de/ Puma Hoodie
http://www.yeezys.eu/ Yeezys
http://www.yeezychaussureadidas.fr/ Basket Adidas
http://www.tommyhilfiger-outlet.us/ Tommy Hilfiger Outlet
http://www.supremeclothingshop.us/ Supreme Hoodie
http://www.offwhite-hoodie.us/ Off White Shoes
http://www.converseallstar.fr/ Converse
http://www.bottes-ugg.fr/ Botte UGG
http://www.filaschuhe.de/ Fila Pullover
http://www.pradabags.org.uk/ Prada Shoes
http://www.supremehoodie.org.uk/ Supreme Clothing
http://www.the-northface.us/ North Face
http://www.nikeschuheairmax.de/ Schuhe Nike
http://www.air-max.fr/ Air Max
http://www.scarpeadidas.eu/ Scarpe Adidas
http://www.vans-canada.ca/ Vans Shoes
http://www.toryburch-outlet.us/ Tory Burch Flip Flops
http://www.pandora-charms.ca/ Pandora Bracelet
http://www.stevemaddensneakers.us/ Steve Madden Slip Ons
http://www.riverislandshoes.co.uk/ River Island Coats
http://www.scarpevans.eu/ Vans
http://www.scarpenikeairmax.eu/ Nike
http://www.skechers-boots.us/ Skechers Shoes
http://www.tomsboots.us/ Toms Sale
http://www.uggbootsstore.us/ UGG Boots
http://www.puma-canada.ca/ Puma Shoes
http://www.pradapurse.us/ Prada Handbags
http://www.thenorth-face.fr/ Veste The North Face
http://www.scarpehogan.eu/ Hogan Uomo
http://www.superdryjacket.us/ Superdry Sale
http://www.adidas-yeezy.de/ Adidas Jacke
http://www.riverislandsale.co.uk/ River Island Shoes
http://www.borsemichaelkors.eu/ Michael Kors Borse
http://www.supremeclothing-uk.co.uk/ Supreme UK
http://www.pumarihannafenty.us/ Puma Rihanna
http://www.doudounethenorthface.fr/ Doudoune The North Face
http://www.saucony-shoes.us/ Saucony Shoes
http://www.suicoke-sandals.us/ Suicoke Womens
http://www.superdryjackets.co.uk/ Superdry Sale
http://www.thenorthface-jacke.de/ The North Face
http://www.skecherssandals.co.uk/ Skechers UK
http://www.reebok-classic.us/ Reebok Shoes
http://www.ralphlauren-poloshirts.us/ Ralph Lauren Dresses
http://www.adidasschuheherren.de/ Adidas Ultra Boost
http://www.ugg-uk.co.uk/ UGG Boots UK
http://www.vibramshoes.us/ Vibram Boots
http://www.vibramshoes.us.com/ Vibram 5 Fingers
http://www.underarmour.us.com/ Under Armour Shirts
http://www.pandorajewelryofficialsite.us/ Pandora
http://www.northface-jacke.de/ The North Face Rucksack
http://www.prada-purse.us/ Prada Handbags
http://www.tommyhilfigerdresses.us/ Tommy Hilfiger Dresses
http://www.swarovskicrystaloutlet.us/ Swarovski Rings
http://www.vansshoes-outlet.us/ Vans Shoes
http://www.superdryhoodie.co.uk/ Superdry Jacket
http://www.underarmour-outlet.ca/ Under Armour Canada
http://www.skechersoutletcanada.ca/ Skechers Go Walk
http://www.salvatoreferragamo.org.uk/ Salvatore Ferragamo Belt
http://www.redbottomschristianlouboutin.us/ Christian Louboutin Shoes
http://www.salomonshoes.us/ Salomon XA PRO 3D
http://www.bijouxpandora2019.fr/ Bague Pandora
http://www.pandora-outlet.us/ Pandora Rings
http://www.swarovskijewelryoutlet.us/ Swarovski Crystal
http://www.schuhe-nike.de/ Nike Air Max
http://www.riverislandclothes.us/ River Island Jeans
http://www.uggslipperscanada.ca/ UGG Slippers
http://www.offwhiteshirt.us/ Off White Clothing
http://www.uggslippersoutlet.us/ UGG Outlet
http://www.salvatore-ferragamo.co.uk/ Ferragamo
http://www.riverislanddresses.co.uk/ River Island Dresses
http://www.yeezyboost350.fr/ Yeezy Boost
http://www.swarovskicrystalcanada.ca/ Swarovski
http://www.adidasyeezyschuhe.de/ Adidas Schuhe
http://www.sperryoutlet.us/ Sperry Boat Shoes
http://www.balenciagaus.us/ Balenciaga Sneakers
http://www.vansshoes.org.uk/ Vans Old Skool
http://www.salomonshoes.org.uk/ Salomon Speedcross
http://www.pandoraringsuk.co.uk/ Pandora
http://www.underarmourtracksuit.co.uk/ Under Armour Tracksuit
http://www.pandora-canada.ca/ Pandora Rings
http://www.prada-canada.ca/ Prada
http://www.anellipandora.eu/ Pandora
http://www.underarmourtrainers.co.uk/ Under Armour Tracksuit
http://www.conversefemme.fr/ Converse
http://www.off-whiteshoes.us/ Off White Hoodie
http://www.pandoracharms-outlet.us/ Pandora Charms
http://www.yeezymafia.us/ Yeezy Boost 350
http://www.yezzys.org.uk/ Yeezy Trainers
http://www.offwhiteshoes.org.uk/ Off White T Shirt
http://www.pumafentyshoes.us/ Puma
http://www.scarpesaucony.eu/ Scarpe Running
david님의 댓글
david 작성일
http://www.vibramshoes.us.com/ Vibram Running Shoes
http://www.anellipandora.eu/ Collane Pandora
http://www.sperryoutlet.us/ Sperry
http://www.underarmourtrainers.co.uk/ Under Armour Trainers
http://www.redbottomschristianlouboutin.us/ Louboutin
http://www.vans-canada.ca/ Vans Shoes
http://www.the-northface.org.uk/ North Face Jacket
http://www.underarmour-outlet.ca/ Under Armour Stock
http://www.salvatoreferragamo.org.uk/ Salvatore Ferragamo Shoes
http://www.yeezymafia.us/ Yeezy Mafia
http://www.tommyhilfigerdresses.us/ Tommy Hilfiger Sweatshirt
http://www.pandorajewelrycom.us/ Pandora Jewelry
http://www.timberlandshoes.co.uk/ Timberland
http://www.uggbootsstore.us/ UGGS On Sale
http://www.yeezyboost350.fr/ Yeezy Boost 350
http://www.scarpesaucony.eu/ Scarpe Running
http://www.reebok-classic.us/ Reebok
http://www.scarpehogan.eu/ Hogan Donne
http://www.uggslipperscanada.ca/ UGG Boots
http://www.vibramshoes.us/ Vibram 5 Fingers
http://www.pandorajewelryofficialsite.us/ Pandora Official Site
http://www.vansshoes-outlet.us/ Vans Shoes
http://www.toryburch-outlet.us/ Tory Burch Handbags
http://www.prada-purse.us/ Prada
http://www.offwhite-hoodie.us/ Off White Shirt
http://www.adidas-yeezy.fr/ Chaussure Adidas
http://www.riverislandshoes.co.uk/ River Island Shoes
http://www.superdryclothing.us/ Superdry Coats
http://www.scarpevans.eu/ Vans Slip On
http://www.nikeschuheairmax.de/ Air Max
http://www.prada-canada.ca/ Prada Sunglasses
http://www.bottes-ugg.fr/ Botte UGG
http://www.ultra-boost.us/ Adidas Ultra Boost
http://www.supremehoodie.org.uk/ Supreme Hoodie
http://www.conversefemme.fr/ Converse Blanche
http://www.puma.org.uk/ Puma Shoes
http://www.superdryhoodie.co.uk/ Superdry Hoodie
http://www.thenorth-face.fr/ Doudoune The North Face
http://www.pandora-outlet.us/ Pandora Earrings
http://www.riverislandclothes.us/ River Island Jeans
http://www.timberlandbootsstore.us/ Timberland Shoes
http://www.scarpeadidas.eu/ Yeezy Boost 350 V2
http://www.pandorajewelryoutlet.us.org/ Pandora Charms
http://www.the-northface.us/ North Face Backpack
http://www.tomsboots.us/ Toms Store
http://www.stevemaddensneakers.us/ Steve Madden Sneakers
http://www.supremeclothingshop.us/ Supreme Jacket
http://www.riverislandsale.co.uk/ River Island Shoes
http://www.underarmour.us.com/ Under Armour Sweatshirt
http://www.northface-jacke.de/ North Face Regenjacke
http://www.sperry.us.org/ Sperrys Women
http://www.pandora-canada.ca/ Pandora
http://www.valentinosandals.us/ Valentino Heels
http://www.tommyhilfiger-outlet.us/ Tommy Hilfiger
http://www.swarovskicrystaloutlet.us/ Swarovski Jewelry
http://www.reeboks.us/ Reebok Classic
http://www.pandoraringsuk.co.uk/ Pandora Rings
http://www.ugg-uk.co.uk/ UGG Boots
http://www.salomonshoes.org.uk/ Salomon Speedcross
http://www.adidasyeezyschuhe.de/ Adidas Yeezy
http://www.saucony-shoes.us/ Saucony Running Shoes
http://www.superdryjacket.us/ Superdry Sale
http://www.pradapurse.us/ Prada Handbags
http://www.supremehoodiestore.us/ Supreme
http://www.supremeclothing-uk.co.uk/ Supreme UK
http://www.supremeclothingcanada.ca/ Supreme Canada
http://www.doudounethenorthface.fr/ Manteau North Face
http://www.underarmourtracksuit.co.uk/ Under Armour UK
http://www.balenciagaus.us/ Balenciaga Bags
http://www.poloralph-lauren.us/ Ralph Lauren Polo Shirts
http://www.salomonshoes.us/ Salomon
http://www.riverislanddresses.co.uk/ River Island Dresses
http://www.adidasschuheherren.de/ Adidas Yeezy
http://www.uggslippersoutlet.us/ UGGS For Men
http://www.salvatore-ferragamo.co.uk/ Salvatore Ferragamo Shoes
http://www.vans-shoes.ca/ Vans Slip On
http://www.puma-shoes.co.uk/ Puma
http://www.pumaschuhedamen.de/ Puma Hoodie
http://www.yeezys.eu/ Yeezy Boost 350 V2
http://www.swarovskijewelryoutlet.us/ Swarovski Crystal
http://www.reebok.org.uk/ Reebok Outlet
http://www.michaelkorsborse.eu/ Michael Kors Borse
http://www.scarpe-hogan.eu/ Scarpe Hogan Uomo
http://www.ralphlauren-poloshirts.us/ Ralph Lauren Dresses
http://www.vansshoes.org.uk/ Vans Shoes
http://www.borsemichaelkors.eu/ Michael Kors
http://www.bijouxpandora2019.fr/ Bijoux Pandora
http://www.skechersoutletcanada.ca/ Skechers Outlet
http://www.pandora-charms.ca/ Pandora
http://www.converseallstar.fr/ Converse Noir
http://www.bapehoodieoutlet.us/ Bape Outlet
http://www.swarovskicrystalcanada.ca/ Swarovski Crystal
http://www.pradabags.org.uk/ Prada Shoes
http://www.offwhiteshirt.us/ Off White Hoodie
http://www.pumafentyshoes.us/ Puma
http://www.off-whiteshoes.us/ Off White Hoodie
http://www.suicoke-sandals.us/ Suicoke Sale
http://www.yeezychaussureadidas.fr/ Basket Adidas
http://www.toryburchhandbags.us/ Tory Burch
http://www.adidas-yeezy.de/ Adidas Schuhe
http://www.thenorthface-jacke.de/ The North Face Jacke
http://www.offwhiteshoes.org.uk/ Off White Hoodie
http://www.schuhe-nike.de/ Air Max
http://www.filaschuhe.de/ Fila Winterschuhe
http://www.scarpenikeairmax.eu/ Nike Scarpe
http://www.yezzys.org.uk/ Yeezy Boost 350
http://www.chaussurenikeofficiel.fr/ Air Max 97
http://www.skechers-boots.us/ Skechers Outlet
http://www.puma-canada.ca/ Puma Shoes
http://www.ralphlaurenshirt.org.uk/ Ralph Lauren Hoodie
http://www.superdryjackets.co.uk/ Superdry Coats
http://www.skecherssandals.co.uk/ Skechers Shoes
http://www.pandoracharms-outlet.us/ Pandora Outlet
http://www.air-max.fr/ Shaussure Nike
http://www.pumarihannafenty.us/ Puma Shoes
frank님의 댓글
frank 작성일
http://www.eccosandals.us/ Ecco Sandals
http://www.bapeclothing.co.uk/ Bape Clothing
http://www.hydroflaskuk.co.uk/ Hydro Flask
http://www.air-max90.us/ Air Max 95
http://www.bapehoodie.org.uk/ Bape Jacket
http://www.bose.org.uk/ Bose Bluetooth Speaker
http://www.monclersale.us/ Moncler Coat
http://www.championhoodie.org.uk/ Champion Sweater
http://www.hydroflasks.ca/ Hydro Flask Water Bottle
http://www.championsweatshirt.co.uk/ Champion Clothing
http://www.fendibags.us/ Fendi Shoes
http://www.canadagoosejacketsoutlet.us/ Canada Goose Sale
http://www.adidasyeezy.us/ Yeezy 500
http://www.hugobosssuits.us/ Hugo Boss Outlet
http://www.jordan-11.us.com/ Jordan 11
http://www.fjallraven-backpack.us/ Fjallraven
http://www.calvinkleinunderwear.org.uk/ Calvin Klien
http://www.brooks-shoes.us/ Brooks Tennis Shoes
http://www.birkenstocksandals-outlet.us/ Birkenstock Sandals
http://www.clarks-outlet.co.uk/ Clarks Boots
http://www.champion-sweatshirt.us/ Champion Sweatsuit
http://www.fitflopshoes.co.uk/ Fitflop
http://www.calvinklein-dresses.us/ Calvin Klein Underwear
http://www.adidascanadaoutlet.ca/ Yeezy Canada
http://www.cartiercanada.ca/ Cartier Love Ring
http://www.goyard-bags.co.uk/ Goyard Wallet
http://www.coachbags.org.uk/ Coach Bags
http://www.north-facejacket.us/ North Face Outlet
http://www.karenmillenoutlet.us/ Karen Millen Outlet
http://www.eccoshoes-outlet.us/ Ecco Shoes
http://www.burberrybags.org.uk/ Burberry
http://www.fjallravenkankenofficialsite.us/ Fjallraven Kanken
http://www.balenciagas.org.uk/ Balenciaga Bags
http://www.goldengoose.org.uk/ Golden Goose
http://www.asicsrunningshoes.co.uk/ Asics Kayano
http://www.karenmillenuk.org.uk/ Karen Millen
http://www.adidas-yeezy.co.uk/ Yeezy Shoes
http://www.lululemonleggingsoutlet.us/ Lululemon Sale
http://www.bvlgari-jewelry.us/ Bvlgari Jewelry
http://www.columbiaclothing.us/ Columbia
http://www.champion-hoodie.us/ Champion T Shirt
http://www.goyardbagsstore.us/ Goyard Bags
http://www.bose-wirelessheadphones.us/ Bose Bluetooth Headphones
http://www.northfaceoutlet.co.uk/ North Face Backpack
http://www.conversetrainers.co.uk/ Converse Trainers
http://www.longchamp.org.uk/ Longchamp Bags
http://www.ferragamoshoes.ca/ Salvatore Ferragamo
http://www.canadagoosejacketuk.co.uk/ Canada Goose UK
http://www.boseheadphones.co.uk/ Bose Headphones
http://www.jackwolfskin.org.uk/ Jack Wolfskin UK
http://www.northfacebackpack.us/ North Face Jacket
http://www.monclercoat.co.uk/ Moncler
http://www.asicscanadashoes.ca/ Asics Gel Kayano
http://www.montblancpens.org.uk/ Mont Blanc Fountain Pen
http://www.northfacejackets.org.uk/ North Face Outlet
http://www.northfacejacketsoutlet.us/ The North Face
http://www.converse-canada.ca/ White Converse
http://www.lululemonpants.ca/ Lululemon Yoga Mat
http://www.merrell-shoes.us/ Merrell Shoes
http://www.nikecanadaoutlet.ca/ Nike Shoes
http://www.fjallraven-kanken.org.uk/ Fjallraven Bags
http://www.louboutintrainers.org.uk/ Louboutin Trainers
http://www.burberry-scarf.co.uk/ Burberry Scarf
http://www.coachpurses.us/ Coach Handbags
http://www.giuseppe-shoes.us/ Guiseppes
http://www.katespadenewyork.us/ Kate Spade Outlet
http://www.coachbags-outlet.us/ Coach Wallet
http://www.lebron-17.us/ Lebron James Shoes
http://www.monclerjacketwomens.us/ Moncler
http://www.birkenstocksandals-sale.us/ Birkenstock Shoes
http://www.fitflop-sandals.us/ Fitflop Shoes
http://www.balenciagashoes.org.uk/ Balenciaga Trainers
http://www.asicstrainers.co.uk/ Asics Trainers
http://www.converseallstar.us/ Converse All Star
http://www.ecco-shoes.ca/ Ecco Sandals
http://www.katespadebags.co.uk/ Kate Spade Bags
http://www.bapehoodie.ca/ Bape Hoodie
http://www.airmax90.co.uk/ Air Max 97
http://www.hydroflaskwaterbottle.us/ Hydro Flask Water Bottle
http://www.championtshirt.us/ Champion T Shirt
http://www.adidas-zxflux.us/ Adidas Gazelle
http://www.addidasnmd.us/ Adidas Shoes
http://www.katespadebags.org.uk/ Kate Spade Handbags
http://www.jordan-33.us/ Jordan 13
http://www.airmax2020.us/ Air Max 720
http://www.lululemons.us/ Lululemon Shorts
http://www.championsweatshirt.us/ Champion Shoes
http://www.bose-canada.ca/ Bose Soundlink
http://www.mizunousa.us/ Mizuno Shoes
http://www.canadgoosejacket.us/ Canada Goose
http://www.calvinkleincanada.ca/ Calvin Klein Dresses
http://www.adidasstasmith.us/ Adidas Stan Smith
http://www.cartier-lovebracelet.us/ Cartier Love Bracelet
http://www.mont-blanc.org.uk/ Mont Blanc Fountain Pen
http://www.filaclothing.us/ Fila Clothing
http://www.filashoesshirt.us/ Fila Sneakers
http://www.goldengoose-sale.us/ Golden Goose Sneakers
http://www.mcmbackpackbags.us/ MCM Wallet
http://www.hugobossjeans.us/ Hugo Boss T Shirt
http://www.fitflopshoessandals.us/ Fitflop Slippers
http://www.jordan-shoes.ca/ Jordan Shoes
http://www.airmax270sale.us/ Nike Air Max
http://www.air-max720.us/ Nike Air Max
http://www.fila-canada.ca/ Fila Hoodie
http://www.jordan-11.org.uk/ Jordan Retro 11
http://www.boseheadphonesstore.us/ Bose Headphones
http://www.giuseppe.org.uk/ Giuseppe Shoes
http://www.michaelkors-purse.us/ Michael Kors Purse
http://www.longchampbackpackbags.us/ Longchamp Tote
http://www.converseshoes-outlet.us/ Converse Slip On
http://www.birkenstocksale.co.uk/ Birkenstock Sale
http://www.laurenralphlauren.us/ Polo Ralph Lauren
http://www.clarks-canada.ca/ Clarks Wallabees
http://www.nike-shoes.org.uk/ Nike Air Max
http://www.championhoodie.ca/ Champion T Shirt
http://www.asicswomensshoes.us/ Womens Asics
http://www.airmax270.ca/ Nike Air Max
http://www.boseheadphones.ca/ Bose Headphones
http://www.jackwolfskinjackets.org.uk/ Jack Wolfskin Coat
http://www.karenmillendresses.us/ Karen Millen
http://www.katespade-bags.ca/ Kate Spade
http://www.goldengoosesneakerssale.co.uk/ Golden Goose Sneakers Sale
http://www.goyardbags.org.uk/ Goyard Tote
http://www.canadagoose-jacket.ca/ Canada Goose Parka
http://www.christianlouboutinheels.us/ Christian Louboutin Heels
http://www.birkenstocksale.org.uk/ Birkenstock
http://www.clark-shoes.us/ Clarks Shoes
http://www.juicycouturetracksuit.us/ Juicy Couture Outlet
http://www.fjallravenkanken.ca/ Fjallraven Backpack
http://www.bapeshirt.us.com/ Bape Jacket
http://www.bottegaveneta-handbags.us/ Bottega Veneta
http://www.calvin-klein.org.uk/ Calvin Klien
http://www.adidasshoes.org.uk/ Adidas Tracksuit
http://www.curry6-shoes.us/ Curry 6
http://www.goldengoosetrainers.co.uk/ Golden Goose Superstar
http://www.balenciaga-shoes.ca/ Balenciaga
http://www.katespade-canada.ca/ Kate Spade Handbags
http://www.montblancpensoutlet.us/ Mont Blanc Pens
http://www.bosestore.us/ Bose Wireless Headphones
http://www.filashoes.org.uk/ Fila
http://www.columbiajackets.us/ Columbia Clothing
http://www.lacoste-shoes.us/ Lacoste Outlet
http://www.fendishoes.us/ Fendi
http://www.hydroflask-sale.us/ Hydro Flask
http://www.merrellboots.us/ Merrell Sandals
http://www.lacosteoutlet.us/ Lacoste Clothing
http://www.adidas-yeezy.ca/ Adidas Yeezy
http://www.juicycoutureoutlet.us/ Juicy Couture Outlet
http://www.nikeuk-trainers.org.uk/ Nike Shoes
http://www.fjallravenbackpack.co.uk/ Fjallraven Backpack
http://www.karenmillendresses.org.uk/ Karen Millen Dresses
http://www.birkenstocksandals.ca/ Birkenstock Sandals
http://www.hydro-flask.org.uk/ Hydro Flask 21 OZ
http://www.michaelkorshandbagsoutlet.us/ Michael Kors Outlet
http://www.ferragamos.us/ Ferragamo Sandals
james님의 댓글
james 작성일
http://www.puma-shoes.co.uk/ Puma Suede
http://www.skechers-boots.us/ Skechers
http://www.valentinosandals.us/ Valentino Heels
http://www.salvatore-ferragamo.co.uk/ Ferragamo
http://www.conversefemme.fr/ Converse Pas Cher
http://www.adidasyeezyschuhe.de/ Adidas Yeezy
http://www.toryburch-outlet.us/ Tory Burch Bags
http://www.bijouxpandora2019.fr/ Pandora Bracelet
http://www.timberlandbootsstore.us/ Timberlands Womens
http://www.supremeclothingshop.us/ Supreme Coats
http://www.the-northface.org.uk/ North Face Jacket
http://www.reebok-classic.us/ Reebok Sneakers
http://www.toryburchhandbags.us/ Tory Burch
http://www.pandora-outlet.us/ Pandora Rings
http://www.pandorajewelryofficialsite.us/ Pandora Charms
http://www.stevemaddensneakers.us/ Steve Madden Sneakers
http://www.pradabags.org.uk/ Prada
http://www.bottes-ugg.fr/ Botte UGG
http://www.vibramshoes.us.com/ Vibram Five Finger Shoes
http://www.offwhiteshirt.us/ Off White Shoes
http://www.vansshoes.org.uk/ Vans Shoes
http://www.pandoracharms-outlet.us/ Pandora Charms
http://www.superdryjackets.co.uk/ Superdry Coats
http://www.tommyhilfiger-outlet.us/ Tommy Hilfiger Hoodie
http://www.vansshoes-outlet.us/ High Top Vans
http://www.ralphlauren-poloshirts.us/ Ralph Lauren Dresses
http://www.supremehoodiestore.us/ Supreme Hoodie
http://www.swarovskicrystaloutlet.us/ Swarovski Crystal
http://www.tommyhilfigerdresses.us/ Tommy Hilfiger Outlet
http://www.underarmourtracksuit.co.uk/ Under Armour Tracksuit
http://www.scarpe-hogan.eu/ Hogan Outlet
http://www.pandora-charms.ca/ Pandora Charms
http://www.adidas-yeezy.fr/ Yeezy Boost 350 V2
http://www.bapehoodieoutlet.us/ Bape Outlet
http://www.nikeschuheairmax.de/ Schuhe Nike
http://www.sperryoutlet.us/ Sperrys Men
http://www.scarpeadidas.eu/ Scarpe Adidas
http://www.riverislandshoes.co.uk/ River Island Shoes
http://www.pandora-canada.ca/ Pandora
http://www.riverislanddresses.co.uk/ River Island Dresses
http://www.uggslipperscanada.ca/ UGG Shoes
http://www.timberlandshoes.co.uk/ Timberland Boots
http://www.salomonshoes.org.uk/ Salomon Hiking Boots
http://www.superdryhoodie.co.uk/ Superdry UK
http://www.pumarihannafenty.us/ Puma Rihanna
http://www.swarovskijewelryoutlet.us/ Swarovski Jewelry
http://www.thenorth-face.fr/ The North Face
http://www.pandorajewelryoutlet.us.org/ Pandora Official Site
http://www.reebok.org.uk/ Reebok Outlet
http://www.poloralph-lauren.us/ Ralph Lauren Outlet
http://www.suicoke-sandals.us/ Suicoke Shoes
http://www.skecherssandals.co.uk/ Skechers UK
http://www.pandorajewelrycom.us/ Pandora Charms
http://www.ugg-uk.co.uk/ UGG Slippers
http://www.anellipandora.eu/ Pandora Anelli
http://www.adidas-yeezy.de/ Adidas Yeezy
http://www.the-northface.us/ North Face Coats
http://www.underarmour.us.com/ Under Armour Outlet
http://www.sperry.us.org/ Sperry
http://www.swarovskicrystalcanada.ca/ Swarovski Canada
http://www.yeezychaussureadidas.fr/ Chaussure Adidas
http://www.puma-canada.ca/ Puma Rihanna
http://www.yeezys.eu/ Yeezy Boost 350 V2
http://www.chaussurenikeofficiel.fr/ Air Max 97
http://www.balenciagaus.us/ Balenciaga Shoes
http://www.redbottomschristianlouboutin.us/ Red Bottom Shoes
http://www.riverislandclothes.us/ River Island Dresses
http://www.pandoraringsuk.co.uk/ Pandora Earrings
http://www.uggbootsstore.us/ UGG Slippers
http://www.pumaschuhedamen.de/ Puma Suede
http://www.supremeclothing-uk.co.uk/ Supreme UK
http://www.underarmour-outlet.ca/ Under Armour Stock
http://www.offwhiteshoes.org.uk/ Off White Shoes
http://www.superdryjacket.us/ Superdry Hoodie
http://www.yeezymafia.us/ Yeezy Shoes
http://www.supremehoodie.org.uk/ Supreme New York
http://www.filaschuhe.de/ Fila Schuhe
http://www.air-max.fr/ Nike Air Max
http://www.prada-purse.us/ Prada Purse
http://www.vibramshoes.us/ Vibram Five Finger Shoes
http://www.scarpehogan.eu/ Hogan Uomo
http://www.offwhite-hoodie.us/ Off White Shirt
http://www.tomsboots.us/ Toms Sale
http://www.pumafentyshoes.us/ Puma Fenty
http://www.reeboks.us/ Reebok Shoes
http://www.salomonshoes.us/ Salomon
http://www.converseallstar.fr/ Converse Femme
http://www.scarpevans.eu/ Vans
http://www.superdryclothing.us/ Superdry Hoodie
http://www.uggslippersoutlet.us/ UGG Outlet
http://www.saucony-shoes.us/ Saucony Womens Shoes
http://www.scarpenikeairmax.eu/ Air Max
http://www.vans-canada.ca/ Vans
http://www.northface-jacke.de/ The North Face
http://www.schuhe-nike.de/ Nike Air Max
http://www.pradapurse.us/ Prada Purse
http://www.yeezyboost350.fr/ Adidas Yeezy
http://www.riverislandsale.co.uk/ River Island Coats
http://www.salvatoreferragamo.org.uk/ Salvatore Ferragamo
http://www.michaelkorsborse.eu/ Tracolla Michael Kors
http://www.supremeclothingcanada.ca/ Supreme Canada
http://www.scarpesaucony.eu/ Saucony Scarpe
http://www.yezzys.org.uk/ Yeezy
http://www.vans-shoes.ca/ Vans
http://www.skechersoutletcanada.ca/ Skechers Go Walk
http://www.underarmourtrainers.co.uk/ Under Armour Outlet
http://www.off-whiteshoes.us/ Off White Shoes
http://www.adidasschuheherren.de/ Yeezy Schuhe
http://www.puma.org.uk/ Puma Sneakers
http://www.borsemichaelkors.eu/ Tracolla Michael Kors
http://www.ultra-boost.us/ Ultra Boost 4.0
http://www.prada-canada.ca/ Prada Canada
http://www.doudounethenorthface.fr/ Doudoune North Face
http://www.thenorthface-jacke.de/ The North Face Schuhe
http://www.ralphlaurenshirt.org.uk/ Ralph Lauren Hoodie
karina님의 댓글
karina 작성일
http://www.bapeshirt.us.com/ Bape Shirt
http://www.columbiaclothing.us/ Columbia Coats
http://www.boseheadphones.co.uk/ Bose Wireless Headphones
http://www.lebron-17.us/ Lebron 17
http://www.canadgoosejacket.us/ Canada Goose Outlet
http://www.bapehoodie.ca/ A Bathing Ape
http://www.brooks-shoes.us/ Brooks Tennis Shoes
http://www.airmax2020.us/ Air Max 720
http://www.hydroflask-sale.us/ Hydro Flask 40 OZ
http://www.conversetrainers.co.uk/ Converse High Tops
http://www.eccosandals.us/ Ecco
http://www.boseheadphones.ca/ Bose Canada
http://www.calvinklein-dresses.us/ Calvin Klein Shoes
http://www.championhoodie.org.uk/ Champion
http://www.jordan-shoes.ca/ Jordan Shoes
http://www.calvinkleincanada.ca/ Calvin Klein
http://www.lululemonpants.ca/ Lululemon Leggings
http://www.fila-canada.ca/ Fila Canada
http://www.northfacejacketsoutlet.us/ North Face Sale
http://www.jackwolfskin.org.uk/ Jack Wolfskin Parka
http://www.converseshoes-outlet.us/ Converse Slip On
http://www.champion-hoodie.us/ Champion T Shirt
http://www.boseheadphonesstore.us/ Bose Wireless Headphones
http://www.curry6-shoes.us/ Jordan Shoes
http://www.air-max720.us/ Air Max 270
http://www.fitflopshoes.co.uk/ Fitflop
http://www.coachpurses.us/ Coach Bags
http://www.filashoes.org.uk/ Fila Clothing
http://www.cartiercanada.ca/ Cartier Love Ring
http://www.ecco-shoes.ca/ Ecco Canada
http://www.birkenstocksandals-outlet.us/ Birkenstock
http://www.giuseppe-shoes.us/ Guiseppes
http://www.katespadebags.org.uk/ Kate Spade Bags
http://www.nike-shoes.org.uk/ Air Max 97
http://www.hydroflasks.ca/ Hydro Flask
http://www.birkenstocksandals-sale.us/ Birkenstock Sale
http://www.ferragamoshoes.ca/ Salvatore Ferragamo Shoes
http://www.christianlouboutinheels.us/ Christian Louboutin Heels
http://www.goyard-bags.co.uk/ Goyard Bags
http://www.air-max90.us/ Air Max 90
http://www.adidas-yeezy.co.uk/ Adidas Yeezy
http://www.juicycouturetracksuit.us/ Juicy Couture Jewelry
http://www.airmax90.co.uk/ Air Max 270
http://www.jordan-11.org.uk/ Jordan Shoes
http://www.burberry-scarf.co.uk/ Burberry Bags
http://www.hugobosssuits.us/ Hugo Boss
http://www.bose-canada.ca/ Bose Canada
http://www.michaelkorshandbagsoutlet.us/ Michael Kors Purse
http://www.adidas-yeezy.ca/ Adidas Canada
http://www.asicstrainers.co.uk/ Asics Running Shoes
http://www.goldengoose.org.uk/ Golden Goose
http://www.longchampbackpackbags.us/ Longchamp Tote
http://www.clark-shoes.us/ Clarks Outlet
http://www.bose-wirelessheadphones.us/ Bose Car Speakers
http://www.lacoste-shoes.us/ Lacoste Outlet
http://www.fendishoes.us/ Fendi Shoes
http://www.giuseppe.org.uk/ Giuseppe Shoes
http://www.canadagoosejacketuk.co.uk/ Canada Goose Parka
http://www.northfacejackets.org.uk/ North Face Backpack
http://www.laurenralphlauren.us/ Polo Ralph Lauren
http://www.bose.org.uk/ Bose Headphones
http://www.katespade-canada.ca/ Kate Spade Wallet
http://www.mcmbackpackbags.us/ MCM Handbags
http://www.hydroflaskwaterbottle.us/ Hydro Flask
http://www.filashoesshirt.us/ Fila Shirt
http://www.fendibags.us/ Fendi Boots
http://www.goldengoose-sale.us/ Golden Goose Shoes
http://www.goyardbagsstore.us/ Goyard Tote
http://www.columbiajackets.us/ Columbia
http://www.katespade-bags.ca/ Kate Spade Canada
http://www.championhoodie.ca/ Champion Hoodie Canada
http://www.coachbags.org.uk/ Coach Bags
http://www.goldengoosesneakerssale.co.uk/ Golden Goose Sneakers
http://www.fjallraven-kanken.org.uk/ Fjallraven Kanken Backpack
http://www.adidasyeezy.us/ Adidas Yeezy
http://www.canadagoose-jacket.ca/ Canada Goose Parka
http://www.championtshirt.us/ Champion Shoes
http://www.championsweatshirt.co.uk/ Champion
http://www.coachbags-outlet.us/ Coach Purses
http://www.karenmillenoutlet.us/ Karen Millen Dresses
http://www.jordan-33.us/ Jordan 11
http://www.juicycoutureoutlet.us/ Juicy Couture Outlet
http://www.jackwolfskinjackets.org.uk/ Jack Wolfskin Fleece
http://www.lululemons.us/ Lululemon Yoga Mat
http://www.adidasstasmith.us/ Adidas Shoes
http://www.fjallravenkankenofficialsite.us/ Fjallraven
http://www.clarks-outlet.co.uk/ Clarks Sandals
http://www.adidasshoes.org.uk/ Adidas Shoes
http://www.burberrybags.org.uk/ Burberry UK
http://www.mizunousa.us/ Mizuno Wave Rider
http://www.birkenstocksale.co.uk/ Birkenstock
http://www.karenmillendresses.us/ Karen Millen Coats
http://www.converse-canada.ca/ Converse Canada
http://www.fjallravenkanken.ca/ Fjallraven Kanken Backpack
http://www.michaelkors-purse.us/ Michael Kors Purse
http://www.eccoshoes-outlet.us/ Ecco Shoes
http://www.merrell-shoes.us/ Merrell Outlet
http://www.balenciagashoes.org.uk/ Balenciaga
http://www.nikecanadaoutlet.ca/ Nike Canada
http://www.converseallstar.us/ Converse All Star
http://www.goyardbags.org.uk/ Goyard London
http://www.karenmillenuk.org.uk/ Karen Millen Tops
http://www.bvlgari-jewelry.us/ Bvlgari Bracelet
http://www.clarks-canada.ca/ Clarks Sandals
http://www.adidascanadaoutlet.ca/ Adidas Outlet
http://www.calvin-klein.org.uk/ Calvin Klein Underwear
http://www.fitflop-sandals.us/ Fitflop Slippers
http://www.louboutintrainers.org.uk/ Christian Louboutin Shoes
http://www.asicsrunningshoes.co.uk/ Asics Kayano
http://www.monclersale.us/ Moncler T Shirt
http://www.birkenstocksale.org.uk/ Birkenstock Sandals
http://www.balenciagas.org.uk/ Balenciaga
http://www.bapehoodie.org.uk/ Bape Shirt
http://www.champion-sweatshirt.us/ Champion Sweatshirt
http://www.jordan-11.us.com/ New Jordans
http://www.fjallravenbackpack.co.uk/ Fjallraven Backpack
http://www.karenmillendresses.org.uk/ Karen Millen Outlet
http://www.ferragamos.us/ Ferragamo
http://www.katespadenewyork.us/ Kate Spade Outlet
http://www.hydro-flask.org.uk/ Hydro Flask 21 OZ
http://www.cartier-lovebracelet.us/ Cartier Love Bracelet
http://www.bosestore.us/ Bose Wireless Headphones
http://www.northfaceoutlet.co.uk/ North Face Jacket
http://www.katespadebags.co.uk/ Kate Spade Handbags
http://www.championsweatshirt.us/ Champion T Shirt
http://www.adidas-zxflux.us/ Adidas ZX Flux
http://www.lululemonleggingsoutlet.us/ Lululemon Leggings
http://www.goldengoosetrainers.co.uk/ Golden Goose Sneakers
http://www.asicscanadashoes.ca/ Asics Gel Nimbus
http://www.fitflopshoessandals.us/ Fitflop Sandals
http://www.addidasnmd.us/ Adidas NMD
http://www.birkenstocksandals.ca/ Birkenstock Sale
http://www.monclerjacketwomens.us/ Moncler Outlet
http://www.hydroflaskuk.co.uk/ Hydro Flask
http://www.canadagoosejacketsoutlet.us/ Canada Goose Outlet
http://www.longchamp.org.uk/ Longchamp Backpack
http://www.nikeuk-trainers.org.uk/ Nike Shoes
http://www.calvinkleinunderwear.org.uk/ Calvin Klein Dresses
http://www.bottegaveneta-handbags.us/ Bottega Veneta Bags
http://www.north-facejacket.us/ North Face Jacket
http://www.airmax270sale.us/ Nike Air Max
http://www.northfacebackpack.us/ North Face
http://www.montblancpens.org.uk/ Mont Blanc Pen
http://www.airmax270.ca/ Air Max 97
http://www.hugobossjeans.us/ Hugo Boss Shoes
http://www.bapeclothing.co.uk/ Bape Shirt
http://www.asicswomensshoes.us/ Asics Shoes
http://www.montblancpensoutlet.us/ Mont Blanc Ballpoint Pen
http://www.merrellboots.us/ Merrell Boots
http://www.fjallraven-backpack.us/ Fjallraven Kanken Backpack
http://www.monclercoat.co.uk/ Moncler Jacket
http://www.lacosteoutlet.us/ Lacoste Shoes
http://www.filaclothing.us/ Fila Shoes
http://www.balenciaga-shoes.ca/ Balenciaga Shoes
http://www.mont-blanc.org.uk/ ont Blanc Pen
linda님의 댓글
linda 작성일
http://www.fjallravenkankenuk.org.uk/ Fjallraven Uk
http://www.adidastrainersoutlet.org.uk/ Adidas Trainers
http://www.brooksshoes.org.uk/ Brooks Ravenna 9
http://www.belstaff.org.uk/ Belstaff Sale
http://www.suicokesandals.ca/ Suicoke Sandals
http://www.newbalanceshoes.us.com/ New Balance
http://www.supreme-clothing.ca/ Supreme Shirt
http://www.ecco-canada.ca/ Ecco Golf Shoes
http://www.fjallravenbackpack.us.org/ Fjallraven Kanken Mini
http://www.curry7.us.com/ Curry 5
http://www.michaelkorshandbags.ca/ Michael Kors Bags
http://www.adidasnmd.us/ Adidas Nmd
http://www.hydroflasksale.us.org/ Hydro Flask 32 Oz
http://www.riverislanddresses.org.uk/ River Island Dresses
http://www.niketrainersoutlet.org.uk/ Air Max
http://www.golden-goose.ca/ Golden Goose Sale
http://www.clarksshoescanada.ca/ Clarks Canada
http://www.birkenstock-canada.ca/ Birkenstock Shoes
http://www.pandoracanada-jewelry.ca/ Pandora Canada
http://www.katespadebagscanada.ca/ Kate Spade Handbags
http://www.nikeshox.us.org/ Nike Shox Mens
http://www.christian-louboutin.us.org/ Red Bottoms
http://www.newbalance.us.org/ New Balance 247
http://www.columbiajackets.us.com/ Columbia Fleece Jacket
http://www.belstaffjackets.org.uk/ Belstaff Jacket
http://www.birkenstock.us.org/ Birkenstock Shoes
http://www.brooksshoes.ca/ Brooks Beast
http://www.karenmillendressesoutlet.co.uk/ Karen Millen Coats
http://www.bosesoundlink.ca/ Bose Soundlink Mini 2
http://www.bape-clothing.us.com/ Bape Sweater
http://www.goldengoose-sneakers.co.uk/ Golden Goose
http://www.pandoracanada-charms.ca/ Pandora Rings
http://www.pandoracanadacharmsjewelry.ca/ Pandora Jewelry Canada
http://www.woolrichparka.us/ Woolrich Parka
http://www.air-max270.us.org/ Nike Air Max 90
http://www.canadagoose-canada.ca/ Canada Goose Outlet
http://www.geox-shoes.us/ Geox Sneakers
http://www.air-max.org.uk/ Nike Air Max
http://www.ralphlaurencanadaoutlet.ca/ Polo Ralph Lauren Canada
http://www.air-max.us.org/ Air Max 97
http://www.bape-hoodie.co.uk/ Bape
http://www.brooksrunningshoes.co.uk/ Brooks Running Shoes
http://www.coach-bags.co.uk/ Coach Purses
http://www.pandoracharmsonline.us/ Pandora
http://www.beatssolo3wireless.us/ Beats Headphones
http://www.golden-goosesneakers.us.org/ Golden Goose Sale
http://www.merrellshoes.us.com/ Merrell Shoes
http://www.adidassuperstar.us.org/ Adidas Superstar Womens
http://www.goldengoose-sneakers.org.uk/ Golden Goose Sneakers Sale
http://www.katespade-bags.us.com/ Kate Spade Purses
http://www.calvin-klein.ca/ Calvin Klein Underwear
http://www.birkenstock-sandals.us.org/ Birkenstock Outlet
http://www.monclerjackets.us.com/ Moncler Coat
http://www.conversetrainers.org.uk/ Converse
http://www.eccocanadashoes.ca/ Ecco Shoes
http://www.ferragamoshoesoutlet.us.org/ Ferragamo Outlet
http://www.uggsboots.us/ Ugg
http://www.longchampsbags.us/ Longchamp Bags
http://www.lecoqsportifshoes.us/ Le Coq Sportif Tennis Shoes
http://www.aldoshoes.us.com/ Aldo
http://www.fjallravenkankencanada.ca/ Fjallraven Kanken Backpack
http://www.adidas.us.org/ Adidas Yeezy
http://www.ferragamo-shoes.org.uk/ Ferragamo
http://www.nikeoffwhite.co.uk/ Off White Belt
http://www.louboutinshoes.ca/ Christian Louboutin
http://www.jewelry-pandora.us.com/ Pandora Jewelry
http://www.northfacecanada.ca/ North Face Outlet
http://www.aldo.us.com/ Aldo Shoes Women
http://www.airmax-720.us.com/ Air Max 270
http://www.brooksshoes.us.com/ Brooks Shoes
http://www.boseheadphones.us.org/ Bose Headphones
http://www.asics-trainers.co.uk/ Asics Trainers
http://www.calvinklein-canada.ca/ Calvin Klein Outlet Canada
http://www.ralphlaurendresses.ca/ Ralph Lauren Dresses
http://www.nikeoutletcanada.ca/ Air Max
http://www.pandorajewelry-store.us/ Pandora Store
http://www.ecco.us.org/ Ecco Sandals
http://www.monclercanada.ca/ Moncler
http://www.offwhite-hoodie.ca/ Off White T Shirt
http://www.beatssolo3.ca/ Beats
http://www.keds-shoes.us/ Kate Spade Keds
http://www.thenorthfacejackets.ca/ North Face Outlet
http://www.calvin-klein.us.org/ Calvin Klien Dresses
http://www.montblanc-pens.org.uk/ Mont Blanc
http://www.coachbagsoutlet.ca/ Coach Purses
http://www.offwhiteshoes.us.org/ Off White Clothing
http://www.fendishirt.us/ Fendi Shirt
http://www.mcmhandbags.us.com/ Mcm
http://www.fjallravenkankenbackpack.co.uk/ Fjallraven Kanken Uk
http://www.adidas-yeezy.us.org/ Yeezy Shoes
http://www.cartierlovering.ca/ Cartier Canada
http://www.conversecanada.ca/ Converse Shoes
http://www.parajumperjacket.us.com/ Pjs Jacket
http://www.birkenstocksandalssale.ca/ Birkenstock Sale
http://www.jimmychoo-shoes.us/ Jimmy Choo Heels
http://www.christian-louboutin.ca/ Red Bottom Shoes
http://www.ecco-shoes.us.org/ Ecco Shoes For Women
http://www.juicycouture.us.org/ Juicy Couture Tracksuit
http://www.katespadehandbags.co.uk/ Kate Spade
http://www.adidasshoes.ca/ Adidas Shoes
http://www.gstar-jeans.us/ G Star
http://www.jordan-shoes.org.uk/ New Jordans
http://www.pandoracharmsofficial.us/ Pandora Charms
http://www.karenmillen-dresses.org.uk/ Karen Millen Dresses
http://www.burberryshirt.co.uk/ Burberry Bags
http://www.skechersshoesoutlet.us.com/ Skechers Outlet
http://www.parajumper.us.com/ Pjs Jacket
http://www.armani.us.org/ Armani Clothing
http://www.longchamp-bags.ca/ Longchamp Purse
http://www.kedssneakers.us/ Keds Boots
http://www.northface-jacket.ca/ North Face Outlet
http://www.hydroflasksale.ca/ Hydro Flask Sale
http://www.beatsheadphones.us.org/ Beats Wireless Headphones
http://www.redbottomshoesforwomen.us/ Christian Louboutin Boots
http://www.uggsbootsforwomen.us.com/ Uggs For Women
http://www.montblancpens.ca/ Mont Blanc Pens
http://www.adidasclothing.us.org/ Adidas Jacket
http://www.northfacejackets.us.com/ North Face Vest
http://www.christianlouboutinredbottomshoes.us/ Christian Louboutin Shoes
http://www.vansoldskool.ca/ Vans
http://www.balenciagashoes.ca/ Balenciaga Sock Shoes
http://www.asicsrunningshoes.ca/ Asics Gel Nimbus
http://www.dieselunderwear.us/ Diesel Underwear
http://www.northfacecoat.co.uk/ North Face Coat
http://www.pandorarings.us.org/ Pandora Charms
http://www.hoganshoes.ca/ Hogan Shoes Outlet
http://www.hogan.us.com/ Hogan Trainers
http://www.bose-headphones.ca/ Bose Bluetooth Headphones
http://www.balenciaga-trainers.co.uk/ Balenciaga Trainers
http://www.pumashoescanada.ca/ Puma Canada
http://www.brooksshoes.us.org/ Brooks Ghost
http://www.champion-hoodie.us.com/ Champion Shoes
http://www.bosesoundlink.org.uk/ Bose Headphones
http://www.pandorajewelrycharms.ca/ Pandora Jewelry
http://www.hugo-boss.us.org/ Hugo Boss Suits
http://www.katespadepurse.us.com/ Kate Spade Purses
http://www.lebron17.ca/ Lebron 17
http://www.coachhandbags.us.com/ Coach Purses
http://www.uggs-onsale.us/ Ugg Boots
http://www.armaniclothing.us/ Armani Dress
http://www.asicsshoes.us.com/ Asics
http://www.hydro-flask.ca/ Hydro Flask Sale
http://www.uggsforwomen.us.org/ Uggs For Women
http://www.ed-hardy.us/ Ed Hardy Jeans
http://www.uggbootssaleuk.co.uk/ Ugg Slippers
http://www.hoganshoesoutlet.co.uk/ Hogan Sneakers
http://www.jordan11.us.org/ New Jordans
http://www.asicsrunningshoes.us.com/ Asics Gel Kayano
http://www.curry7.ca/ Curry 7
http://www.monclers.co.uk/ Moncler T Shirt
http://www.adidas-nmd.ca/ Adidas Nmd R1
linda님의 댓글
linda 작성일
http://www.balenciagasneakers.org/ Balenciaga Shoes
http://www.birkenstock-uk.co.uk/ Birkenstock
http://www.polo-ralphlauren.ca/ Ralph Lauren
http://www.lebron-16.us.org/ Lebron Shoes
http://www.fjallraven.org.uk/ Fjallraven Kanken
http://www.goldengoosesneakers.co.uk/ Golden Goose
http://www.coach-bags.us/ Coach Purses
http://www.skechersshoes-outlet.us/ Skechers Go Walk
http://www.hardenvol3.us/ Harden Vol 2
http://www.hydroflask.in.net/ Hydro Flask 32 OZ
http://www.birkenstockuk.org.uk/ Birkenstock Shoes
http://www.bape.org.uk/ Bape Hoodie
http://www.birkenstocksale.us/ Birkenstock Shoes
http://www.nikeairmaxoutlet.us/ Nike Air Max
http://www.montblanc.org.uk/ Mont Blanc Fountain Pen
http://www.birkenstockcanadasandals.ca/ Birkenstock Sandals
http://www.underarmour-canada.ca/ Under Armour Outlet
http://www.adidas-outlet.ca/ Adidas
http://www.pandora.in.net/ Pandora Jewelry Official Site
http://www.nikeairmaxca.ca/ Nike Canada
http://www.pandorauk-jewelry.co.uk/ Pandora Earrings
http://www.karen-millen.co.uk/ Karen Millen UK
http://www.goldengoosesneakers-sale.us/ Golden Goose
http://www.coachbagsoutlet.us/ Coach Purses
http://www.hydroflask.org.uk/ Hydro Flask Sale
http://www.brooks.us.org/ Brooks Sneakers
http://www.birkenstocksandals-uk.co.uk/ Birkenstock UK
http://www.karenmillendresses.co.uk/ Karen Millen Sale
http://www.fila.in.net/ Fila Mens Shoes
http://www.louboutintrainers.co.uk/ Louboutin Heels
http://www.curry5.ca/ Curry 5
http://www.fjallraven-kanken.co.uk/ Fjallraven
http://www.mizunorunningshoes.us.org/ Mizuno
http://www.bapehoodie.co.uk/ Bape Hoodie
http://www.goldengoose-shoes.us/ Golden Goose
http://www.louboutinredbottoms.us/ Louboutin
http://www.hydro-flask.us.com/ Hydro Flask
http://www.goldengooses.us.org/ Golden Goose Sneakers Sale
http://www.ralphlauren-polo.us/ Lauren Ralph Lauren
http://www.northfacejacket.us.org/ North Face Vest
http://www.ralph-laurencanada.ca/ Lauren Ralph Lauren
http://www.ugg-bootsuk.org.uk/ Ugg UK
http://www.asicsrunningshoes.us/ Asics Shoes
http://www.offwhites.us/ Off White T Shirt
http://www.nikeairmax720.us/ Air Max 720
http://www.airmax-2019.us/ Nike Air Max 2019
http://www.filashoes.co.uk/ Fila Trainers
http://www.vibram-fivefingers.us/ Vibram
http://www.fjallraven.us.com/ Fjallraven Bags
http://www.balenciagatrainers.co.uk/ Balenciaga
http://www.goldengoosesneakers.org.uk/ Golden Goose Trainers
http://www.curry5shoes.us.org/ Curry 5 Shoes
http://www.giuseppeshoes.us.org/ Giuseppe Zanotti
http://www.converse-uk.co.uk/ Converse Trainers
http://www.mcmhandbags.us/ MCM
http://www.jordan-11.us/ New Jordans
http://www.valentinosneakers.us/ Valentino Sandals
http://www.salomon.in.net/ Salomon Shoes
http://www.balenciagashoes.co.uk/ Balenciaga Bags
http://www.goyardcanada.ca/ Goyard Wallet
http://www.coachbags.ca/ Coach Canada
http://www.nikeuk.co.uk/ Nike UK
http://www.saucony.in.net/ Saucony Shoes
http://www.vibram.us.org/ Vibram
http://www.yslbags.us/ Saint Laurent Handbags
http://www.hydroflask.us.org/ Hydro Flask Sale
http://www.yeezy-boost.co.uk/ Yeezy Boost
http://www.ralphlaurencom.us/ Polo Ralph Lauren
http://www.katespade-purses.us.com/ Kate Spade Handbags
http://www.jordanshoesoutlet.us/ New Jordans
http://www.championhoodie.us.com/ Champion
http://www.underarmour.org.uk/ Under Armour Outlet
http://www.yezzys.co.uk/ Yeezy Trainers
http://www.supreme-canada.ca/ Supreme Canada
http://www.birkenstocksandalssale.us/ Birkenstock
http://www.pandorajewelryonline.us/ Pandora Jewelry
http://www.longchampbackpack.us/ Longchamp Tote
http://www.fjallraven-kanken.us.org/ Fjallraven Bags
http://www.off-white.org.uk/ Off White Belt
http://www.airmax95.us.com/ Air Max 97
http://www.giuseppezanotti.org.uk/ Giuseppe Shoes
http://www.yeezycanada.ca/ Adidas Yeezy
http://www.adidasnmdwomens.us/ NMD
http://www.moncler-jacket.org.uk/ Moncler Outlet
http://www.ferragamo.in.net/ Salvatore Ferragamo
http://www.supremeclothingshirt.us.com/ Supreme Clothing
http://www.mulberryhandbags.us/ Burberry Bags
http://www.asicscanada.ca/ Asics Canada
http://www.skecherscanadashoes.ca/ Skechers
http://www.karen-millen.org.uk/ Karen Millen
http://www.calvinkleindresses.us/ Calvin Klein Dresses
http://www.redbottomlouboutinshoes.us/ Red Bottom Shoes
http://www.redbottoms.us.com/ Louboutin
http://www.fjallravenkanken.org.uk/ Fjallraven Backpack
http://www.ultra-boost.co.uk/ Ultra Boost 4.0
http://www.lebron16.ca/ Lebron 16
http://www.timberlandboots.ca/ Timberland Shoes
http://www.championsweatshirt.us.com/ Champion Clothing
http://www.vansoldskool.org.uk/ Vans Trainers
http://www.offwhitecanada.ca/ Off White Shoes
http://www.northfacejacket.us/ North Face
http://www.nikeshoxwomen.us/ Nike Shox Women
http://www.pandoraofficialsite.us/ Pandora Official Site
http://www.pandorarings.us/ Pandora Charms
http://www.valentinoshoessale.us/ Valentino Shoes Sale
http://www.pandoraus.us/ Pandora Charms
http://www.vansoldskool.us.com/ Vans Slip On
http://www.jordan11.org.uk/ Jordan 12
http://www.katespadebags.us/ Kate Spade Handbags
http://www.fitflopshoes.us/ Fitflop Sale
http://www.redbottomsshoes.us/ Louboutin Shoes
http://www.calvinklein.org.uk/ Calvin Klein Bikini
http://www.northfacejacket.co.uk/ North Face Coat
http://www.fitflopsclearance.us/ Fitflop Sandals
http://www.nikecanadashoes.ca/ Nike Shoes
http://www.mizunoshoes.org/ Mizuno Running Shoes
http://www.toms-shoes.us/ Toms Boots
http://www.uggslippers.co.uk/ Ugg Boots
http://www.converses.us/ Converse
http://www.coachcanadabags.ca/ Coach Purses
http://www.fredperry.us.org/ Fred Perry T Shirt
http://www.balenciaga-sneakers.us.org/ Balenciaga Shoes
http://www.yeezyboost350v2.us.com/ Yeezy 350
http://www.vansshoesoutlet.us/ Vans Shoes
http://www.airmax-270.org.uk/ Nike Air Max
http://www.championhoodie.co.uk/ Champion Sweatshirt
http://www.balenciagasneakers.us/ Balenciagas
http://www.burberrybagsuk.co.uk/ Burberry Bags
http://www.adidascanadashoes.ca/ Adidas Canada
http://www.bottegavenetabags.us/ Bottega Veneta Wallet
http://www.fitflopsandals.us/ Fitflop Sale
http://www.yeezy-v3.us/ Yeezy V3
http://www.fjallraven.in.net/ Fjallraven Bags
http://www.longchamp.in.net/ Longchamp Backpack
http://www.yeezytrainers.co.uk/ Yeezy
http://www.kyrie5-shoes.us/ Nike Kyrie
http://www.michaelkors.us.org/ Michael Kors Handbags
http://www.off-white.us.org/ Off White Sneakers
http://www.salomons.us/ Salomon Speedcross 5
http://www.fjallravens.us.org/ Fjallraven Kanken
http://www.valentinoshoes.ca/ Valentino Canada
http://www.kd-11.us.org/ KD 10
http://www.suicoke.us/ Suicoke
http://www.nikeuptempo.us/ Nike Air More Uptempo
http://www.salomon-boots.us/ Salomon Gtx
http://www.adidasultraboost.us.com/ Ultra Boost
http://www.fjallravenkanken.us.com/ Fjallraven
http://www.goyards.co.uk/ Goyard Belt
http://www.hydro-flask.co.uk/ Hydro Flask UK
http://www.fjallraven.us.org/ Fjallraven Kanken Backpack
http://www.goldengoosesneakers.ca/ Golden Goose
http://www.brooksshoes.us/ Brooks
http://www.giuseppe.us.org/ Giuseppe Zanotti
http://www.birkenstockoutlet.us/ Birkenstock Shoes
ronald님의 댓글
ronald 작성일
http://www.beatsstudio3.us/ Powerbeats Pro
http://www.champion-hoodie.ca/ Champion
http://www.northface.us.org/ North Face Coat
http://www.skechers-shoes.us.org/ Skechers Go Walk
http://www.hoganshoessale.co.uk/ Hogan Shoes Outlet
http://www.birkenstocksandals.co.uk/ Birkenstock
http://www.thenorthfacejackets.co.uk/ North Face Backpack
http://www.champion.us.org/ Champion Hoodie
http://www.ferragamo-shoes.ca/ Ferragamo Shoes
http://www.adidasultraboost.ca/ Adidas Canada
http://www.jordan11shoes.ca/ Jordan Shoes
http://www.beatsheadphones.ca/ Beats Solo 3
http://www.kyrie6.us.org/ Kyrie 4
http://www.champion-hoodie.co.uk/ Champion Clothing
http://www.asicsshoes.ca/ Asics Shoes
http://www.hugoboss.us.org/ Hugo Boss Shoes
http://www.airmax-270.ca/ Air Max 270
http://www.salomons.us.com/ Salomon Running Shoes
http://www.monclerpolo.co.uk/ Moncler Outlet
http://www.skechers.us.org/ Skechers Go Walk
http://www.keds.us.com/ Kate Spade Keds
http://www.beatsstudio3.ca/ Powerbeats 3
http://www.ultraboost.ca/ Adidas Ultra Boost
http://www.lebron-17.us.com/ Lebrons James Shoes
http://www.eccoboots.ca/ Ecco Sandals
http://www.coach-bags.us.com/ Coach Outlet
http://www.philipppleinoutlet.org.uk/ Philipp Plein T Shirt
http://www.coach-bags.org.uk/ Coach Handbags
http://www.montblancs.ca/ Mont Blanc Refills
http://www.jordanshoes.us.org/ Jordan Retro
http://www.juicycouturetracksuit.us.com/ Juicy Couture
http://www.nmdshoes.us.com/ Adidas Nmds
http://www.filashoesoutlet.us.com/ Fila Outlet
http://www.ralphlaurenhoodie.org.uk/ Ralph Lauren T Shirt
http://www.pandoracom.us.com/ Pandora Charms
http://www.redbottoms.ca/ Louboutin Shoes
http://www.geoxshoes.us/ Geox Kids Shoes
http://www.adidasyeezyshoes.ca/ Adidas Canada
http://www.pandoraringscanada.ca/ Pandora Rings
http://www.reebok-trainers.org.uk/ Reebok Shoes
http://www.woolrich.us.com/ Woolrich Outlet
http://www.salvatore-ferragamo.org.uk/ Ferragamo
http://www.prada.us.com/ Prada
http://www.mizuno.us.com/ Mizuno Tennis Shoes
http://www.aldoshoesoutlet.us/ Aldo Boots
http://www.bvlgaricanada.ca/ Bvlgari Canada
http://www.eccoshoescanada.ca/ Ecco Shoes Canada
http://www.offwhiteshoes.ca/ Off White T Shirt
http://www.ferragamoshoessale.us/ Ferragamo
http://www.katespadecanadaoutlet.ca/ Kate Spade Phone Case
http://www.river-island.org.uk/ River Island Coats
http://www.offwhitehoodie.us.org/ Off White Shoes
http://www.bosespeakers.co.uk/ Bose Soundsport Wireless
http://www.fitflop.us.org/ Fitflop Sandals
http://www.reebokshoes.ca/ Reebok
http://www.asics-shoes.ca/ Asics Gel Kayano
http://www.bosewirelessheadphones.co.uk/ Bose Quietcomfort 35 Ii
http://www.saucony.us.org/ Saucony Shoes
http://www.pandoracanada.ca/ Pandora Rings
http://www.karenmillen.us.org/ Karen Millen Outlet
http://www.supreme-hoodie.ca/ Supreme Shirt
http://www.michaelkorscanadaoutlet.ca/ Michael Kors Outlet
http://www.hydroflaskcanada.ca/ Hydro Flask Sale
http://www.eccoshoesoutlet.co.uk/ Ecco Trainers
http://www.adidas-shoes.us.org/ Adidas Shoes Women
http://www.northfacehoodie.co.uk/ North Face Backpack
http://www.uggsnowboots.us/ Ugg
http://www.bosewirelessheadphones.us.com/ Bose Headphones
http://www.timberland-boots.ca/ Timberland Boots
http://www.nikeoffwhiteshoes.us.com/ Nike Off White
http://www.goldengoosesale.us.com/ Golden Goose Shoes
http://www.northface-jackets.org.uk/ North Face Backpack
http://www.balenciagacanada.ca/ Balenciagas
http://www.converse-shoes.ca/ Converse All Star
http://www.lebron17shoes.us/ Lebron 17 Shoes
http://www.vansshoes.ca/ Vans Outlet
http://www.bapecanada.ca/ Bape
http://www.uggslippers.org.uk/ Mens Ugg Slippers
http://www.salomons.co.uk/ Salomon Trainers
http://www.uggbootscanada.ca/ Uggs On Sale
http://www.jordanshoes.ca/ Jordan Shoes
http://www.kyrie-6.us/ Nike Kyrie
http://www.supremeclothingoutlet.co.uk/ Supreme Clothing
http://www.cartierlovebracelet.us.org/ Cartier Love Bracelet
http://www.salvatore-ferragamo.ca/ Salvatore Ferragamo Belt
http://www.ralphlaurendresses.us.com/ Polo Ralph Lauren Outlet
http://www.supremehoodie.ca/ Supreme Backpack
http://www.gstarclothing.us/ G Star Jacket
http://www.miumiuhandbags.us.com/ Miu Miu Handbags
http://www.giuseppezanotti.ca/ Giuseppe Zanotti
http://www.goldengoose-sneakers.ca/ Golden Goose Canada
http://www.ferragamo-shoes.co.uk/ Ferragamo Loafers
http://www.stevemaddensandals.us/ Steve Madden Sneakers
http://www.redbottomshoes.ca/ Christian Louboutin
http://www.nikehuarache.ca/ Nike Outlet
http://www.stevemadden-boots.us/ Steve Madden Sandals
http://www.hydroflaskuk.org.uk/ Hydro Flask Lids
http://www.karenmillendressesuk.co.uk/ Karen Millen Dresses
http://www.brooksrunningshoes.us.com/ Brooks Running Shoes
http://www.pumacanada.ca/ Puma Shoes
http://www.thenorthface.us.org/ North Face
http://www.katespade-bags.org.uk/ Kate Spade Handbags
http://www.adidasyeezy.ca/ Adidas Canada
http://www.coachbagscanada.ca/ Coach Purses
http://www.balenciagasneakers.us.org/ Balenciaga Mens Sneakers
http://www.uggs-forwomen.us/ Ugg Slippers
http://www.mizuno-shoes.us.org/ Mizuno Running Shoes
http://www.vans-shoes.org.uk/ Vans Trainers
http://www.giuseppezanotti.us.org/ Guiseppes
http://www.pandorarings.ca/ Pandora Rings
http://www.pandorashop.us/ Pandora Rings
http://www.nikeairmax.co.uk/ Nike Air Force
http://www.ugg-canada.ca/ Uggs On Sale
http://www.louboutinredbottomsshoes.us/ Red Bottom Shoes
http://www.pradabags.ca/ Prada Sunglasses
http://www.fjallravenkankenbackpack.us.com/ Fjallraven Kanken Mini
http://www.pumatrainers.org.uk/ Puma Sneakers
http://www.coach-bags.ca/ Coach Canada
http://www.pandorajewelry.ca/ Pandora Rings
http://www.birkenstock-sandals.ca/ Birkenstock Shoes
http://www.birkenstock-shoes.ca/ Birkenstock Gizeh
http://www.nike-outlet.ca/ Nike Air Max
http://www.merrell.us.org/ Merrell Hiking Boots
http://www.ralphlaurenoutlet.ca/ Ralph Lauren Outlet
http://www.armanishoes.us/ Armani Sunglasses
http://www.yeezyadidas.co.uk/ Yeezy
http://www.katespadebags.ca/ Kate Spade Canada
http://www.moncler-jackets.ca/ Moncler Canada
http://www.puma-shoes.us.org/ Puma Fenty
http://www.supreme-hoodie.co.uk/ Supreme Clothing
http://www.fjallraven-canada.ca/ Fjallraven Kanken Backpack
http://www.pandorajewelrywebsite.us/ Pandora Website
http://www.vansoldskool.us.org/ Vans
http://www.nikecanadaairmax.ca/ Nike Canada
http://www.pandorajewelryofficial.us/ Pandora Charms
http://www.longchamp-bags.org.uk/ Longchamp
http://www.toms.us.org/ Toms Slippers
http://www.converse-shoes.us.org/ Converse Shoes
http://www.vansoldskool.co.uk/ Vans Old Skool
http://www.bosespeakers.ca/ Bose
http://www.supreme-hoodie.us.org/ Supreme Clothing
http://www.jimmychoo.us.org/ Jimmy Choo Boots
http://www.pandorajewelryca.ca/ Pandora Ca
http://www.vibramshoes.us.org/ Vibram 5 Fingers
http://www.monclerjacketsoutlet.co.uk/ Moncler Jacket
http://www.nikeshoescanada.ca/ Nike Shoes
http://www.mont-blanc.us.org/ Mont Blanc Pens
http://www.filaclothing.us.com/ Fila
http://www.goldengoosesneakerssale.us.org/ Golden Goose Superstar
http://www.ralphlauren-dresses.us/ Polo Ralph Lauren
http://www.wirelessbeats.us/ Powerbeats 3
http://www.hydro-flask.us.org/ Hydro Flask
http://www.philippplein.ca/ Philipp Plein Shoes
http://www.lecoq-sportif.us/ Le Coq Sportif Usa
http://www.adidasshoesoutlet.ca/ Adidas Running Shoes