공학수학 | Runge-Kutta 방법 |
페이지 정보
작성자 cemtool 작성일14-06-11 12:17 조회7,945회 댓글0건본문
다음 미분방정식이 있을 때,
미분방정식의 해를 구하기 위한 4 차 Runge-Kutta 방법의 근사식은 다음과 같다.
여기서 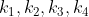 의 조건들이 다음과 같을 때, 4 차 Runge-Kutta 방법을 구현하는 CEMTool 함수 clrk4.cem 을 작성하여라
의 조건들이 다음과 같을 때, 4 차 Runge-Kutta 방법을 구현하는 CEMTool 함수 clrk4.cem 을 작성하여라
. 이 함수의 호출방식은 다음과 같이 하도록 한다. 여기서,
function은 미분방정식을 정의하는 함수의 이름이다.- ex6_8.cem
function; T,Y <> f,a,b,m,y0 /* [T,Y]=clrk4(f,a,b,m,y0) solves Ydot=f(T,Y) on t=[a,b]. INPUTS: f M-file defining input function; interval a,b; m points in interval; y0 initial value OUTPUTS: T abscissa, Y solution by 4th order Runge-Kutta method */ h=(b-a)/(m-1); // Step sizeh T=zeros(m,1); // Column vector of time points Y=zeros(m,1); // Column vector of solution points T(1)=a; Y(1)=y0; for(I=1;I<=m-1;I++){ // There are m-1 steps and m points tI=T(I); // - step through m-1 intervals yI=Y(I); eval(["k1=h*" f "(tI,yI)"]); // Runge-Kutta coefficients eval(["k2=h*" f "(tI+h/2,yI+k1/2)"]); eval(["k3=h*" f "(tI+h/2,yI+k2/2)"]); eval(["k4=h*" f "(tI+h,yI+k3)"]); Y(I+1)=yI+(k1+2*k2+2*k3+k4)/6; T(I+1)=a + h*I; // Next time step }
댓글목록
등록된 댓글이 없습니다.